-
[LG AiMERS] Part 2-2 Matrix Decomposition(SVD, Eigen Decompostion)전공&대외활동 이야기/2024 LG AIMERS 4기 활동 2024. 2. 12. 18:20
본 내용은 LG Aimers 강좌 중, KAIST 신진우 교수님의 강좌 내용을 바탕으로 작성되었습니다
선형대수 관련 내용들을 정리하려고 했었는데, 관련 내용들을 정리하기 전에 간략하게 훑어보는 느낌으로 정리해보려고 한다. 간략한 각 개념들의 정의와 그 흐름만 정리해보았다. 특히 행렬분해에 관련된 내용들을 위주로 작성하였다.
특히 Decomposition에 관해 알아보자.
Decomposition, Factorization(분해)
분해는 하나의 행렬을 두개, 혹은 3개 이상의 행렬 곱으로 행렬을 표현한 것을 의미한다.
A = BC
분해에 관해 알아야하는 이유는 무엇일까?
그 이유는 각 분해를 통해 행렬의 계산의 복잡성을 줄일 수 있기 때문이다.
예를 들어 LU분해의 경우, 일반적으로 L,U모두 가우스 소거법을 쉽게 적용 가능하기에
Ax = b문제를 LUx = b로 바꾸어 Ly = b, y = Ux로 변형하면 쉽게 문제를 풀 수 있다.
다른 예시로 대각행렬의 경우, 행렬의 거듭제곱형을 쉽게 표현가능하다는 장점이 있다.
LU Decompositon(LU분해)
LU 분해는 행렬을 L, U로 분해하는 분해로, 즉, 하삼각행렬(lower triangular matrix) L과 상삼각행렬(Upper Triangular matrix) U의 곱으로 분해하는 방법이다.

행렬을 LU행렬로 분해하는 방법은 여러가지 알고리즘이 존재한다. 하지만, 대다수의 선형대수 교재에서 채택하고 있는 방법은 Gaussian Elimination을 기반으로 한 분해방법이다.



즉, A를 U 형태로 변환하기 위해 Gaussian elimination을 사용하는데 이때, pivot의 값이(더해서 0으로 만드는) Elementary matrix를 구성한다.
이때 E의 역행렬은 그것에 음수를 붙인 형태이기에 L은 E행렬의 곱의 역행렬형태, 즉, 음수를 붙인 형태로 존재한다.
아래의 예시를 보자.


Cholesky Decomposition
Cholesky Decompostion(숄레스키 분해)는 Hermitian matrix와 Postive definite matrix의 분해에서 사용되는 분해로 L과 L의 전치행렬의 곱으로 분해되는 것을 말한다. 보통 LU decomposition과 많이 비교되며, Linear system을 푸는 문제에서 LU분해보다 효율적인 분해로 알려져있다(계산 시간상).

Hermitian matrix(에르미트 행렬)
자기 자신과 켤레 전치(켤레 복소수도 대칭으로 보는)행렬이 같은 복소수 정사각(square) matrix이다. 즉, 일반적인 대칭행렬(symmetric matrix)을 포함하는 상위 개념이다.
이는 고유값들이 항상 실수이고, 고유벡터들은 항상 직교하는 성질을 지니는 성질을 만족한다(스펙트럼 정리의 일부)
에르미트 행렬예시: wiki출처 Positive Definite Matrix(정치행렬) :
고윳값이 양수인 Symmetric(대칭행렬)을 의미한다.Eigen value & Eigen vecetor
아래의 내용들은 고유값과 고유벡터를 기반으로 한 행렬분해방법이기 때문에 고유값과 고유벡터에 관해 간략하게 짚고 넘어가려고 한다.
고유값과 고유벡터에 관한 정의는 다음과 같다.
아래의 Square matrix에 관하여 0벡터가 아닌 벡터 v, 실수 람다가 있다고 하자.

고유값과 고유벡터 위 식을 만족하는 실수 $\lambda를 고유값(eigenvalue), v를 고유벡터라고(eigen vector)라고 한다. 이들을 구하기 위해 eigen decomposition을 거치며, 혹은 특성방정식의 해를 찾기도 한다.
즉, 위의 식을 변형하면

의 식이 나오게 되는데, 이 식 중, 괄호부분의 det가 0이 되는 조건을 찾는 것이 바로 특성방정식이다.

그럼 그 값들의 의미는 무엇일까?
이는 특정한 vector x에 어떠한 선형변환을 했을 때, 크기만 변형시키는, 방향은 변하지 않는 벡터 x를 찾는 것, 그리고 그 크기의 변화량을 찾는 것이 목적이다.

출처: https://angeloyeo.github.io/2019/07/17/eigen_vector.html Diagonal matrix(대각행렬)
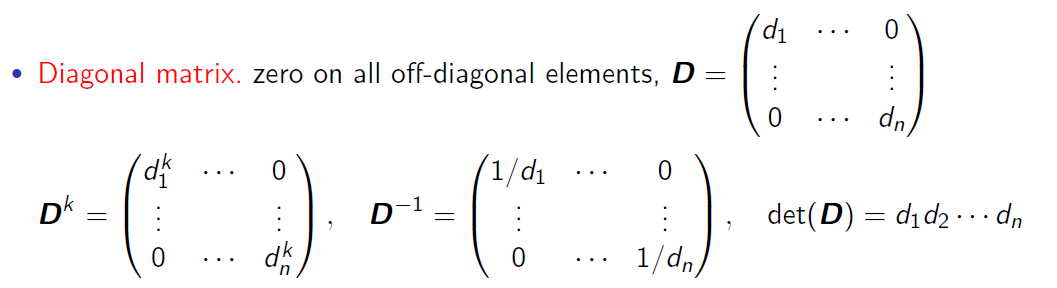
대각 행렬은, 행렬의 주대각선을 제외한 부분들이 모두 0인 행렬로 위에서 보다시피, 매우 유용한 성질들을 가진다.
Diagonalization(대각화)

대각화란, 위에서 보다시피, 행렬이 대각행렬에 있어서 매우 좋은 성질들을 가지기에, 행렬을 대각행렬과 다른 행렬로 분해시키는 것이다. 즉, 적절한 행렬 P와 대각행렬 D를 찾아 아래와 같이 표현하는 것이다.


이런 대각화가 가능한 행렬은 diagonalizable한 행렬이라고 하며 아래의 조건을 가진다.

또한 symmetric한 행렬과 orthogonally diagonalizable한 행렬은 동치이다.
이는 Spectral Theroem을 통해 확인 가능하다.

wiki출처: 스펙트럼정리 이때 U, unitary matrix는 Hermitian matrix와 유사하나, 그 켤레 전치가 역행렬과 같은 복소수 square matrix를 의미한다.
Eigen value Decompositon(고유값 분해)
Square matrix(정방행렬) and exists if we can find a basis of eigenvectors(n개의 선형독립인 고유벡터를 가질때)(such as symmetric matrices)에 관해서 행렬을 고유벡터와 고유값으로 이루어진 행렬로 분해하는 것이다.
즉, 정방행렬에 관해서 이루어지는 분해이다.

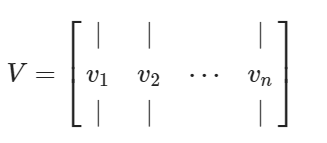

주요 성질로는 위에서 말한 것처럼, 행렬의 거듭제곱꼴을 쉽게 계산가능하게 도와주는 성질이 존재한다.

SVD(Singular Value Decomposition)
Singular value decomposition은 위에서 봤던 여러 분해들이 정방행렬이라는 조건들을 가지고 있었는데, 그렇지 않은 행렬에 관해서도 대각화를 할 수 없을까?라는 의문에서 시작된 분해법이다.

특이값 분해는 직교하는 벡터 집합에 대하여, 선형 변환 후에 그 크기는 변하지만 여전히 직교할 수 있게
되는 그 직교 집합은 무엇인가? 그리고 선형 변환 후의 결과는 무엇인지를 알려주는 분해이다.식의 정의는 다음과 같다, m*n 크기의 행렬에 관항 SVD는 아래 와 같이 정의되며, 각 행렬은 다음과 같다.
U는 orthogoanl matrix이며, $\sigma 는 diagonal matrix, V는 orthogonal matirx이다.
이때, diagonal etries를 이루는 것은 singular value, 즉 특이값이다.
이는 직교하는 행렬 V의 열벡터들의 scaling factor값이다.
즉, 선형변환 전에 직교하는 벡터의 집합은 행렬 V라 하면, 이를 A라는 선형변환을 거칠 때, 여전히 직교하는 정규화된 벡터의 집합을 U라하고, 변환된 크기는 Singular value로 나타내진다라고 할 수 있다.

우리는 결국 SVD를 통해서 m*n행렬을 여러개의 m*n행렬로 분해하면서 각 행렬의 원소의 크기는 Singular value에 의해 결정되게 분해가능하다. 즉, 임의의 행렬 A를 각 정보량에 따라 분해가능함을 의미한다.
이를 이용해 정보를 축소할 수 있다.
EVD와 비교

즉, SVD와 EVD는 정보의 양이라는 관점에서 매우 유사하지만 적용되는 행렬의 조건이 다르다고 할 수 있다.
'전공&대외활동 이야기 > 2024 LG AIMERS 4기 활동' 카테고리의 다른 글
[LG Aimers] 영업성공률 예측 모델 개발기 -전처리를 중심으로 (2) 2024.03.06 [LG Aimers] 영업성공률 예측 모델 개발기 1(해커톤) (0) 2024.02.21 [LgAimers] Casual Inference for Special Cases(다양한 경우에 대한 Causal Inference 적용방법) (1) 2024.01.27 [LGAimers] Calculating Causal Effect(인과추론 계산법) & BackDoor criterion (1) 2024.01.26 [LGAimers] 인과추론에 관한 개념정리 (1) 2024.01.25