[Time-series] Time-series Analysis, 시계열 알아보기

시계열..? 통계부터 시작하자 

시계열 머신러닝, 딥러닝 방법론들이 최근 많이 화재가 되고 있지만 실무적 관점에서는 여전히 통계적 기반의 시계열 분석은 주요한 위치를 차지하고 있으며, 사실 딥러닝, 머신러닝 기법들 또한 해당 방법론을 기반으로 발전된 것들이 많다. 

또한 통계학적 방법론의 가장 큰 장점은 바로 설명력을 기반으로 신뢰성을 가진다는 것이다.

 Alieen Nielsen의 저서 Practical Time Series Analysis을 인용하면 

산업용 시계열 분석은 위험이 낮은 분야에 적용하려고 노력합니다. 광고나 미디어 상품의 출시에 따른 이익을 예측하는 문제에서는 예측의 완전한 검증이 크게 중요하지 않습니다…….(중략)… 통계가 위험이 높은 예측에서 보다 근본적인 역할을 할 수 있기를 바랍니다.

…M4 대회는 시계열 대회로 100,000건의 시계열 데이터셋에 대한 정확도를 예측하는 것이 과제입니다. 이 대회의 우승자는 통계 모델과 신경망의 요소를 결합했습니다. 마찬가지로 준우승을 차지한 사람도 머신러닝과 통계 모두를 포함했습니다. 구체적으로는 통계 모델의 앙상블을 사용했지만…….(후략)

 

즉, 여전히 시계열에서 통계란 빼놓을 수 없기에 관련 내용을 우선 지니고 딥러닝 쪽 논문을 읽으면 좋을 것 같다.

(추가로 사족을 덧붙이자면, 주파수 영역에서 분석하고 분해하고 등등 여러 다른 수학도 잘 쓰이는거 같다)

Time-series data

 Time series data란 무엇인가? Wiki에 따르면 다음과 같다. 

 

In mathematics, a time series is a series of data points indexed (or listed or graphed) in time order. Most commonly, a time series is a sequence taken at successive equally spaced points in time. Thus it is a sequence of discrete-time data. 

즉, 시간에 따른 sequence data이며, continuous time data가 아닌 discrete time data라고 한다(이는 관측이 discrete하기 때문이다). 어 Sequence data하면..! 맞다 NLP가 떠오른다. 최근 많은 방법론들은 Transfomer를 응용하여 Time series를 분석하고 있는데 이에 관해서는 차차 알아보자.

NLP는 time series data의 특수한 case이다.

 

결국 sequence data over time이라는 말로 정의가 될 것이다. 

그렇기에, 과거의 data가 현재에 어떻게 영향을 미치는가가 Time series analysis의 핵심이다. 그렇다면 수식은 아래와 같이 표현 가능하다. 

[DSBA] Lab Seminar 2022: https://www.youtube.com/watch?v=J5Pl5a_mXfE

 

즉, 현재 특정한 시계열 data y는 이전의 y와 외부변수 x와 s(없을 수도 있다)에 의해 결정된다. 

여기서 변수 밑첨자로 붙는 t는 t, 시간에 대해 영향을 받는 변수이다라는 의미이다. 

 

과거의 data? look back window

 

walk foward optimization이라고 불리는 방법은 금융에서 많이 쓰는 용어지만, time series를 보다보면 look back window와 함께 같이 사용된다. 

walk foward는 말 그대로 과거의 데이터 중 일부는 input으로 일부는 output으로 사용하면서 step size만큼 이동하며 성능을 평가하는 방법이다. 

보다 중요한건 look back window로, 이는 과거의 데이터 중 몇개를 볼 것인지를 보는 창문이라고 생각하면 된다. 

만일 fixed - window size를 100으로 정했다고 하자. 

그러면 우리는 측정이 시작된 0일~100(total window size)일까지의 데이터를 우선 가지고 있다고 생각할 수 있다. 

 이 중 70개를 이용해서 30개를 예측하는 모델을 만든다고 하면, 0~70에 해당하는 데이터는 input으로 71~100은 output으로 사용될 것이다. 그러면 이 중 70에 해당하는 것은 look-back window, size 뒷부분, 예측하고자 하는 값의 개수는 look-ahead window size라고 한다. 그리고 다음 step에서는 5~105까지의 data를 쓴다고 하면, 5step을 이동했음으로 이를 step size라고 한다. 

 

정리하면 아래와 같고, 그림을 참고하면 좋다. 

Fixed window size(Total window size): 모델에 사용할 전체 dataset의 크기(batch size?)

Look back window size(input size): 모델에 사용할 input size

Look ahead window size(ouput size): 모델이 예측할 output size

Step size: 데이터 셋을 shift할 크기, 얼마나 이동할 것인가 

Time Series Forecasting (TSF) Using Various Deep Learning Models (2022)

Regression과 관계성 

최근 듣고있는 time series analysis 수업에서 우선 base로 확률과 regression에 관해 듣고 수업을 듣고 있는 중이다. 

그럼 확률과 회귀는 time series와 무슨 관련이 있는 것일까? 

회귀식을 한번 보자. 

다양한 회귀들

 

회귀란 결국 설명하고자하는 변수를 다른 변수들(하나일 수도 있고, 2개일 수도 있다)을 이용해서 설명하고자 하는것이다. 

이를 시계열에 적용하면 설명하고자하는 변수 y를 t, 시간에 관해 설명할 수 있다면, 이것이 시계열 분석일 것이다. 

 

다만, 회귀식은 아래의 그림을 보면 알 수 있듯이, 하나의 x에 수많은 관측값 y가 존재하는 한편, 시계열은 하나의 t라는 변수에 관해 하나의 y만 찍혀있다. 즉, t라는 변수에 y를 단순히 맵핑할 수는 없다. 하지만, 현재의 데이터 y는 과거의 y에 영향을 받았을 것이기에 우리는 수식을 그 둘의 관계로부터 세울 수 있고, 회귀식을 세울 수 있게 된다(y와 x에 관한 표를 y_t와 y_t-1에 관한 표로 구성되어있다고 생각하자)

왼쪽은 회귀, 오른쪽은 시계열이다

Univaritate & Multivariate

즉, 시계열은 이와 같이 회귀식의 form을 많이 가져왔기에, 시계열 모델 또한 비슷한 방식으로 이해할 수 있다. 

Univariate과 Multivariate은 문자 그대로 몇개의 변수를 참조하였는지에 따라 나뉘게 된다. 

처음 들었을 때는, 그럼 forcast를 한 값을 바로 쓰는건가?? 했는데 그건 아니고, 아래와 같이 수식이 구성된다고 생각하면 쉽다. 아래의 예시는 2변수에 관한 multivariate 수식의 예시이다. 

출처: https://www.analyticsvidhya.com/blog/2018/09/multivariate-time-series-guide-forecasting-modeling-python-codes/

즉, y1과 y2를 예측할 때, univariate model이라면 y1의 lagged value만 사용했겠지만, 수식을 보면 알 수 있듯이 Multi variate model의 경우 y1과 y2의 lagged변수를 모두 이용하는 것을 볼 수 있다. 

이를 일반화하면 아래와 같이 표현가능하다.  자세한건 위의 링크를 참조하자!

Single step & Multi step(&Long term time series)

또한 예측하는 변수의 수를 single step, 즉 1개만 예측할지 혹은 여러개를 예측할지에 따라 single과 multi로 표현한다. 

이때 더 먼 미래를 예측하는 경우 long term time series forcasting, LTSF라고 하며, 일반적인 기준은 나와있는 않지만

대다수의 논문을 볼 때 97, 192, 336, 720 step 등을 LTSF의 대표적인 값으로 보는 듯 하다. 

 

또한 예측에 있어서 2가지 방법론이 적용되는데, sequence data에서 예측과 동일하다. 

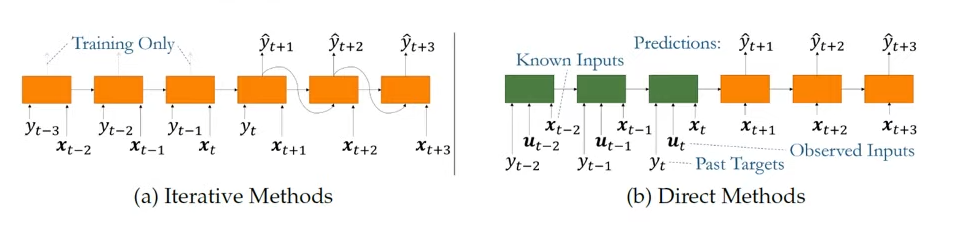
Lim Bryan and Stefan Zohren, "Time series forcasting with deep learning: a servey"

 

Iterative Methods는 train data를 이용해서 다음 data를 순차적으로 예측하는 모델이다. 이때 예측한 결과값을 다음 예측에 동일하게 이용한다. 이런 경우 예측이 올바르지 않을 경우 뒤 부분의 예측이 모두 어긋나는 문제가 생기게 된다. 

 

Direct Method는 Predict의 여러 step에 해당하는 정보들을 동시에 예측하는 방법이다. 즉. ground truth한 input을 받는다. 

Time series의 구성요소(trend, seasonal, cyclical, irregular componet) 

시계열 데이터는 크게 아래의 4가지로 decompose(분해)가 가능하다.

AirPassengers 데이터에 대한 Time series decomposition(출처: https://albertmade.tistory.com/3)

 

Trend(추세): 장기적으로 증가하거나 감소하는 등의 경향성

Seasonal(계절성): 계절적 요인의 영향을 받아, 시간의 흐름에 맞추어 반복적으로 나타나는 패턴

Cyclical(주기성): 정해지지 않은 빈도, 기간으로 일어나는 주기

Irregular component(설명 불가능한 부분, error): Resdiual에 해당하는 부분, 이상적이라면 평균이 0인 정규분포를 따라야하나, 그런 경우는 거의 없다

Cycle vs Seasonality 차이가 뭐야?
책마다, 자료마다, 학자마다 정의가 차이가 있기는 하지만, 일반적으로 Seasonality와 달리, Cycle은 시간의 흐름에 개의치 않으며 포괄적인 개념이다. 즉. 변동이 6개월, 12개월 등 특정 시간적 빈도에 따라 혹은 계절에 따라 변한다면 Seasonality라고 하고 아니면 포괄적으로 Cycle이라고 하는 것 같다. 

Time series의 특징(Temporality, Dimensionality, non Stationaray)

시계열 데이터는 아래의 특징들을 가진다. 

Temporality

시계열 데이터들은 시간 순서대로 관찰된 값들의 집합으로 각 point들은 과거의 값에 dependancy하다. 즉, 연속된 관측치 사이에는 temporal correlation이 존재한다.

Dimensionality

각 time point에서 포착된 데이터들은 하나 혹은 두개 이상의 Attribute를 가진다. 이에 따라 Univariate와 Multivariate를 구분가능하고, Univariate의 경우 예측하고자 하는 변수의 lagged data만 고려하면 되지만, Multivariate의 경우 각 time point간의 관계는 물론, variable 간의 상관관계도 고려해야한다. 

Stationary(정상성)

정상성이란, 쉽게 말해서 '시계열의 특징이 관측된 시간과 무관하다'는 것을 의미하며, 시간이 지나고 Time series data의 통계적 특성이 변하지 않음을 의미한다. 

Stationaryity, 즉 타우 시간 이후에도 동일한 확률분포로 표현된다

통계적 시계열에서는  어떤 확률 과정(Stochastic process)을 따르는 시계열이 있다고 가정하고 그 통계적 과정으로 부터 나타난 표본(Sample)을 통해 그 통계적 과정을 알아내려고 한다. 

우리는 일반적으로 sample들을 다룰 때 iid과정을 많이 적용하는데, 이때 iid 중 identically에 해당하는 동일 확률분포를 가진다~라는 부분에 해당한다. 

 정상성은 Strong stationary와 Weakly stationary가 있으며, 대부분 강 정상성을 만족하는 시계열은 약 정상성을 만족한다고 알려져있다(일부 iid Cauchy 분포 등 예외는 존재). 

 

 Strong stationary의 경우 위와 같이 모든 시간과 무관하게 적률이 일정함을 말한다. 

Weak stationary의 경우는 아래와 같다. 

즉, 매우 완화된 가정을 가지며, 3번의 경우 공분산이 시간의 차이에만 의존(즉, 상관관계가 시간의 차이에 의해서마 ㄴ변화)한다는 것이다. 

검정을 통해 이를 확인 가능하며, KPSS(Kwiatkowski-Phillips-Schmidt-Shin), ADF(Augmented Dicky-Fuller) 검정 등이 존재한다. 대부분의 정상성 검증은 단위근이 존재 유무를 이용해 검정을 한다. 

이때, 단위근이 존재한다면 외부축역으로 인한 오차가 생겼을 때, 시간이 지날 수록 해당 오차가 누적된다. 즉, 아래의 단순 AR(1) 모델을 가정하자. 

이 때, 알파 값이 1보다 작다고 하면, t가 무한대로 가면 error는 0이 된다. 

하지만. 알파가 1 혹은 1보다 크다면 오차는 누적이 된다. 

즉, 아래와 같은 형태가 되며 변동이 한번 발생하면 원상태로 돌아가지 못하게 된다. 이것이 비정상 시계열 데이터이다. 

 

현실적으로 Seasonality, Cycle, Change point 등 변동을 가지는 것이 일반적이기에 정상성을 대다수의 data에서 찾기란 쉽지 않다. 

Some Model 

대표적인 모델들은 아래와 같고, 해당 모델들의 관한 간단한 리뷰는 차후 진행할 예정이다. 

1. Autoregressive (AR) : 시계열의 이전 값과 이후 값 사이 어느 정도의 상관 관계(자기 상관)가 있을 때 사용
2. Autoregressive Integrated Moving Average (ARIMA) : 시계열 예측에 있어 가장 많이 사용되고 알려진 모델  AR(p)(Auto regression) 모델과 MA(q) (Moving Average) 모델, 그리고 차분(ARIMA의 핵심)이 결합된 모형
3. Seasonal Autoregressive Integrated Moving Average (SARIMA) : ARIMA에 계절성을 확장시킨 모델
4. XGBoost 등 앙상블 계열 모델
5. CNN 등 이미지 기반 모델
6. RNN, LSTM, GRU 기반 모델
7. Transfomer 기반 모델들: Infomer 등
8. GCN 등 생성 모델 기반
9. ARCH와 GARCH: 금융모델에서 대표적인 전통모델 

 

참고 자료

 

Time series analysis 전공수업

MINDSCALE: 단위근 검정

딥러닝 전에, 알아보자 시계열 분석! – (1) 시작하자 시계열!