-
[PyTorchZerotoAll 내용정리] 09: Softmax ClassifierML&DL 이야기/Pytroch 2023. 9. 5. 13:13

MNIST Dataset 한번 쯤은 들어봤을 dataset이다 06, 07 내용에 이은 Softmax Classifier이다.
Logistic Reression은 단일 품목을 labeling하기 위한 방법이었다. 예시를 들면 개인지, 개가 아닌지?를 판단하는 모델을 학습하는 것이었다.
하지만 우리는 때에 따라서 해당 동물의 사진이 개인지, 고양이인지, 토끼인지, 두더쥐인지 다양한 품목, 종류에 대해 판명해야할 때도 많다. 이를 위해 우리는 Soft max 함수가 필요하고, 이러한 문제를 multi-classification problem, 혹은 model이라고 한다.

x에 맞추어 출력이 10개인 것이 합당할 것이다 기존 classification 문제와 달리 그러면 multi-classfication문제이기 때문에 우리가 분류해야하는 n개의 label에 맞게 n차원의 output을 내야할 것이다.

가중치의 수는 어떻게 해야할까?? 기존의 classification 식에 해당하는 왼쪽 행렬의 식을 보면 w는 $R^{2\times1}$이다. 그 이유는 행렬의 곱셈 원리에 의해서 우리의 x가 $R^{N\times2}$이고, y가 $R^{N\times1}$이기 때문이다.
그럼 multi classfication에서 변하는 것은 output y가 $R^{N\times10}$(10은 우리가 분류해야하는 class의 수다)이기에 이에 맞추어 w또한 $R^{m\times10}$의 형태로 바뀐다.
$$w = R^{m\times10}$$
Softmax
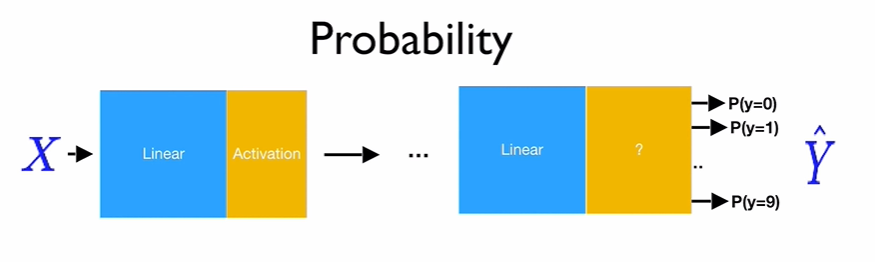
우리의 목표 우리의 목표는 위의 그림처럼 확률로 output을 바꾸는 것이다. Softmax function은 아래와 같이 우리의 결과를 확률로 해석하게 변경해준다.

Softmax function 출력이 n차원으로 표현될 때, 이를 어떻게 확률로 표현할 수 있을까?? 이를 해결하는 것이 softmax함수이다. 정확히는 softmax activation function이다.
softmax function의 식을 보면 Softmax의 출력은 0~1 사이의 실수이며, 그 총합이 1이 된다. 즉, output을 '확률'로 해석할 수 있음을 알 수 있다.
즉, 시그모이드 함수의 총합을 이용하는 generalized된 버전인 것이다(k=2인 경우 시그모이드와 식이 동일하다)

시그모이드(로지스틱함수)와 Softmax의 관계 출처: https://financial-engineering.medium.com/ml-softmax-%EC%86%8C%ED%94%84%ED%8A%B8%EB%A7%A5%EC%8A%A4-%ED%95%A8%EC%88%98-2f4740141bfe Sigmoid함수의 유도식 및 Softmax의 유도에 관해 설명한 내 다른 게시글이다.
https://secundo.tistory.com/69
[ML] Regression과 Logit(승수)와 Sigmoid함수 그리고 Softmax함수
https://kevinitcoding.tistory.com/entry/%EB%94%A5-%EB%9F%AC%EB%8B%9D%EC%9D%84-%EC%9C%84%ED%95%9C-%ED%9A%8C%EA%B7%80-%EB%B6%84%EC%84%9D%EC%9D%98-%EC%9D%B4%ED%95%B4-Logit-Sigmoid-Softmax https://www.youtube.com/watch?v=K7HTd_Zgr3w 딥 러닝을 위한 회귀
secundo.tistory.com
LSE(Real soft max)
(참조만 할것)
Real softmax라고도 불리는 LogSumExlp(LSE) 함수는 아래와 같다.
$$\ln \sum_{i=1}^{k} \exp \left(x_{i}\right)$$
LSE 함수는 최댓값 함수(ReLU)에 근사(smooth approximation)하도록 동작한다

soft max는 max함수의 근사함수이다 Softmax의 목적은 최대값을 미분가능한 근사치를 제공하는 것이다(exp이용). 미분이 불가능한 함수를 가능하도록 바꿈으로 인해 Max 함수를 사용하는 모델을 최적화 할 수 있다(동시에 convex함수이며, 단조증가한다)
Softmax Activation function
softmax의 정의를 찾아보면 아래와 같다(wiki기준 23.09.05)
The softmax function,also known as softargmax or normalized exponential function,
converts a vector of K real numbers into a probability distribution of K possible outcomes즉, k가 나올 확률로 k개의 실수를 변경해주는 식이다(다시 말해 결과값을 정규화시켜준다)
식을 보면 아래와 같다.
$$\frac{\exp \left(a_{k}\right)}{\sum_{i=1}^{n} \exp \left(a_{i}\right)}$$
$$p_{i}=\frac{e^{z_{i}}}{\sum_{j=1}^{k} e^{z_{j}}} \ \ for \ \ i=1, 2, ... k$$
k는 클래스의 수, z는 소프트맥수 함수의 입력값으로 각 index에 해당하는 input값이다.
이를 직관적으로 해석하면 j번째 입력값/입력값의 총합으로 볼 수 있으며 이는 곧 확률관점으로 위의 식을 해석할 수 있게 해준다(위에서 정의된 LSE함수를 x에 관해 편미분하면 softmax의 식이 유도된다. 이는 LSE의 gradient가 Softmax function이라는 뜻이다)
하지만 실제로 smooth maximum하지는 아니고, smooth arg max 함수이기에, soft arg max함수라고 부르자는 사람도 있다고 한다.
1. Softmax 활성화 함수는 기존 LSE함수의 gradient이다.
2. Softmax 활성화 함수는 특정 조건에서, 큰 input은 강조하고, 작은 input은 억제한다. 이는 Softmax 함수와 유사한 방식으로 작동한다.
3. Softmax의 출력은 0~1 사이의 실수이며, 이 output을 '확률'로 해석할 수 있다.
4. 소프트맥스 활성화 함수를 적용해도 원소의 대소 관계는 변하지 않는다(단조 증가함수이기에)주의점: Overflow
Softmax 활성화 함수는 지수 함수를 사용하기 때문에, 컴퓨터로 계산을 할 때 오버플로 문제가 생길 수 있다. 예를 들어 은 무한대를 뜻하는 inf가 된다.
이를 해결하기 위해 입력 신호 중 최댓값을 이용하여 해당 값으로 전체를 입력값을 빼준다.
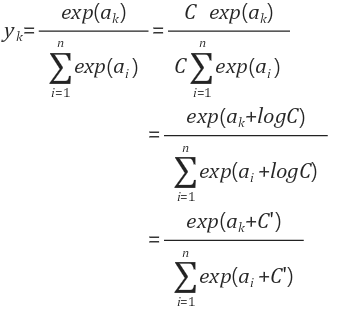
변형된 softmax 함수 식, C'은 input의 max값이다 예시로 300, 200, 500으로 input이 들어온다면, 이를 변형하여 -200, -300, 0으로 변경하는 식이다
아래는 코드 예시이다.
def softmax(x): c = np.max(x) # 오버플로 방지를 위한 식 # max값을 빼준다 exp_x = np.exp(x-c) sum_exp_x = np.sum(exp_x) y = exp_x / sum_exp_x return yCalculate Loss

1-hot label을 얻기 위한 구성 오차를 계산하는 과정은 위의 그림과 같다. 우리가 구한 y의 예측치와 y의 실제값(one-hot encdoing)을 비교할 것이다.
이때 오차 계산에 있어 우리는 Cross EntropyLoss 혹은 NLLLoss를 오차함수로 사용할 것이다.
Cross EntropyLoss VS NLL Loss
공식문 서를 보면 Cross Entropy Loss와 NLL Loss 의 설명이 적혀있다.
해당 내용 중에 Cross Entropy Loss에 관한 설명은 다음과 같이 젹혀있다.

Cross-Entropy = LogSoftmax + NLL Loss라는 이야기인가??
그렇다.
정리하면
nn.CrossEntropyLoss
- LogSoftmax가 포함되어 있는 식
- Input : ( f(x), target )
- target 은 input 의 shape에 따라 다양한 형태가 가능
nn.NLLLoss
- LogSoftmax가 포함되어 있지 않음
- Input : ( LogSoftmax(f(x)), target )
- 나머진 nn.CrossEntropyLoss 와 유사함
그럼으로 아래를 주의해서 사용하자.
- CrossEntropyLoss 안에서 LogSoftmax와 Negative Log-likelihood 가 진행되기 때문에 softmax layer나 log 함수가 적용되지 않은 모델 output(raw data)을 input으로 주어야 한다
- 이와 달리 NLLLoss 안에서는 softmax나 log함수가 이뤄지지 않는다. 그래서 모델 output(raw data)을 input으로 그대로 사용하는 것이 아니라 LogSoftmax 함수를 output layer로 적용한 후 NLL Loss의 input으로 사용해야한다.
Code Implement(with pytorch)
MNIST 예시로 Softmax를 적용하였다(두 loss function의 경우를 모두 작성하였다)
https://colab.research.google.com/drive/1QB72fSRQTZihbzbp8qf7cf-jRWZFy4Ax#scrollTo=DlW0pSpXyGoP
Google Colaboratory Notebook
Run, share, and edit Python notebooks
colab.research.google.com
코드 작성 시 주의점:
1. Linear Model의 output자체가 이미 logit이다. 두번 logit하지 말자
2. NLL Loss 사용시 log_softmax가 필요하다, 그 이유는 logx와 x를 비교해야하기 때문이다.
Cross Entropy사용시 코드
from __future__ import print_function from torch import nn, optim, cuda from torch.utils import data from torchvision import datasets, transforms import torch.nn.functional as F import time class Net(nn.Module): def __init__(self): super(Net, self).__init__() self.l1 = nn.Linear(784, 520) self.l2 = nn.Linear(520, 320) self.l3 = nn.Linear(320, 240) self.l4 = nn.Linear(240, 120) self.l5 = nn.Linear(120, 10) def forward(self, x): x = x.view(-1, 784) # Flatten the data (n, 1, 28, 28)-> (n, 784) x = F.relu(self.l1(x)) x = F.relu(self.l2(x)) x = F.relu(self.l3(x)) x = F.relu(self.l4(x)) return self.l5(x) model = Net() model.to(device) criterion = nn.CrossEntropyLoss() optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5) def train(epoch): model.train() for batch_idx, (data, target) in enumerate(train_loader): data, target = data.to(device), target.to(device) optimizer.zero_grad() output = model(data) loss = criterion(output, target) loss.backward() optimizer.step() if batch_idx % 10 == 0: print('Train Epoch: {} | Batch Status: {}/{} ({:.0f}%) | Loss: {:.6f}'.format( epoch, batch_idx * len(data), len(train_loader.dataset), 100. * batch_idx / len(train_loader), loss.item())) def test(): model.eval() test_loss = 0 correct = 0 for data, target in test_loader: data, target = data.to(device), target.to(device) output = model(data) # sum up batch loss test_loss += criterion(output, target).item() # get the index of the max pred = output.data.max(1, keepdim=True)[1] correct += pred.eq(target.data.view_as(pred)).cpu().sum() test_loss /= len(test_loader.dataset) print(f'===========================\nTest set: Average loss: {test_loss:.4f}, Accuracy: {correct}/{len(test_loader.dataset)} ' f'({100. * correct / len(test_loader.dataset):.0f}%)')NLL Loss 사용시
class Net(nn.Module): def __init__(self): super(Net, self).__init__() self.l1 = nn.Linear(784, 520) self.l2 = nn.Linear(520, 320) self.l3 = nn.Linear(320, 240) self.l4 = nn.Linear(240, 120) self.l5 = nn.Linear(120, 10) def forward(self, x): x = x.view(-1, 784) # Flatten the data (n, 1, 28, 28)-> (n, 784) x = F.relu(self.l1(x)) x = F.relu(self.l2(x)) x = F.relu(self.l3(x)) x = F.relu(self.l4(x)) return self.l5(x) model = Net() model.to(device) criterion = F.nll_loss optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5) def train(epoch): model.train() for batch_idx, (data, target) in enumerate(train_loader): data, target = data.to(device), target.to(device) optimizer.zero_grad() logit = model(data) output = F.log_softmax(logit, dim=1) //차이부분! loss = criterion(output, target) loss.backward() optimizer.step() if batch_idx % 10 == 0: print('Train Epoch: {} | Batch Status: {}/{} ({:.0f}%) | Loss: {:.6f}'.format( epoch, batch_idx * len(data), len(train_loader.dataset), 100. * batch_idx / len(train_loader), loss.item())) def test(): model.eval() test_loss = 0 correct = 0 for data, target in test_loader: data, target = data.to(device), target.to(device) logit = model(data) output = F.log_softmax(logit, dim=1) # sum up batch loss test_loss += criterion(output, target).item() # get the index of the max pred = output.data.max(1, keepdim=True)[1] correct += pred.eq(target.data.view_as(pred)).cpu().sum() test_loss /= len(test_loader.dataset) print(f'===========================\nTest set: Average loss: {test_loss:.4f}, Accuracy: {correct}/{len(test_loader.dataset)} ' f'({100. * correct / len(test_loader.dataset):.0f}%)')'ML&DL 이야기 > Pytroch' 카테고리의 다른 글