[ML] Regression과 Logit(승수)와 Sigmoid함수 그리고 Softmax함수

https://kevinitcoding.tistory.com/entry/%EB%94%A5-%EB%9F%AC%EB%8B%9D%EC%9D%84-%EC%9C%84%ED%95%9C-%ED%9A%8C%EA%B7%80-%EB%B6%84%EC%84%9D%EC%9D%98-%EC%9D%B4%ED%95%B4-Logit-Sigmoid-Softmax

https://www.youtube.com/watch?v=K7HTd_Zgr3w 

딥 러닝을 위한 회귀 분석의 이해: Logit, Sigmoid, Softmax

아래 내용은 위의 영상과 블로그 및 아래의 여러 블로그들을 참고하여 작성되었습니다. 

 

Regression 회귀란

ML에서 다루는 Task는 크게 2가지로 나눌 수 있다. 첫번째는 회귀, 두번째는 분류이다. 

회귀 분석의 경우 종속 변수와 독립 변수 사이의 내재된 인과관계가 있다고 가정할 때 이를 이용한 수식을 찾아내는 것이다. 

이 경우 수식이 얼마나 엄밀한가를 확인하기 위해 각 요소들에 관한 오차를 제곱해서 모두 합한, MSE를 보통 척도로 사용한다. 

대다수 우리가 생각하는 회귀 분석은 종속변수를 실수형으로 상정한다. 

즉, 이에 따라서 아래의 형태를 띈다(다변량회귀분석)

$$ y = a_1*x_1 + a_2*x_2 + .... a_n*x_n + \epsilon$$

위 식에서 $x_n$은 각 Feature를 의미하고 $\epsilon$은 bias라고 불린다.

위 수식의 회귀 식은 현재 선형회귀함수로 보이지만, 이를 비선형으로 표현할 수도 있다. 예를 들어 $x_2=x_1^2$이면 그러하다, 반대로 비선형을 선형관계가 있는 것으로 표현도 가능한데, 이를 Feature Engineering이라고 한다. 즉, 독립벼눗를 어떻게 잡느냐에 따라서 선형과 비선형 관게를 변경할 수도 있다.

Logistic Regression == Classification

보통 Regression model과 Classfication을 분리하여 공부하고는 하는데, 로지스틱 회귀(Logistic Regression)는 종속 변수가 범주형(Category)인 경우 사용할 수 있는 회귀 분석 방법이다. 

이것이 가능하려면 우리는 기존 Regression model의 결과가 여러 Class의 확률을 나타낼 수 있게 해야한다. 

즉 아래로 식을 변형 할 수 있다. 

$$ P(x) = a_1*x_1 + a_2*x_2 + .... a_n*x_n + \epsilon$$

문제는 P(x)는 확률이기에 [0,1]의 값을 가져야하지만 선형회귀 식은 [-∞, +∞]의 값을 가진다. 이 때문에 우리는 범위를 맞추어주어야한다는 필요가 생긴다, 

이것이 Odds(승산)이다. 

Odds

https://analysisbugs.tistory.com/167

[머신러닝] Odds (오즈) 란?

확률이면서 양의 무한대 값을 가지는 개념으로 수식은 아래와 같다. 

즉, 만일 내가 관심있는 사건이 발생한 횟수 / 그것의 여사건의 수로 계산을 하는 것이다. 

이를 확률로 계산할 수도 위의 식처럼 확률로 계산 가능한데, 반대로 Odds를 알면 확률을 계산하는 것도 쉽게 가능하다. 

 Odds의 경우 p가 1에 가까울 수록 분모가 0에 가까워지기에 범위는 [0, + ∞ ]이다. 

문제는 아래 그림과 같이 대칭성이 맞지 않는다는 것이다. 

만일 관심있는 사건이 1번일어나고 6번이 일어나지 않으면 0.17이지만, 반대로 관심있는 사건이 6번 일어나고 관심 없는 사건이 1번 일어날 경우 Odds는 6이 된다. 

즉, 관심있는 사건에 관한 가중이 너무 큰것이다. 이를 해결하기 위해 Odds의 log를 붙이 Logits이 나온다. 

Logits

$$Logit = ln(odds) = ln(\frac{p}{1-p})$$

위에서 말했듯 수식은 위와 같다. 이 경우 log변환을 하면 같은 case에서 0을 기준으로 대칭성을 가진다는 것을 확인 가능하다. 또한 Logits을 취하게 되면 위의 회귀식과 동일한 범위인 [-∞,+∞] 값의 범위를 가지게 된다.

Logistic Regression(Sigmoid 함수)

로짓을 이용하게 되면서 우리는 확률을 예측하는 회귀모델식을 변형하여 아래와 같이 세울 수 있게 되었다.

Logistic Regression Form

그럼 이를 우리가 궁금한 p에 관한 식으로 정리하기 위해 역함수를 취하면 아래와 같은 식을 얻을 수 있다. 

Logitic 식 변형하기

마지막으로 위의 식에서 회귀식에 해당하던 부분을 X로 치환하면 우리가 아는 Sigmoid함수의 형태로 변형된다. 

Sigmoid함수는 인공신경망에서 다음의 두가지 역할을 가진다. 

 

첫 번째, 인공 신경망의 활성화 함수로 사용된다. 시그모이드 함수는 신경망의 가중치가 바뀌는 과정(학습)에 연속성을 부여합니다. 초기 신경망 모델은 계단 함수와 같은 비연속적인 활성 함수를 사용했고 학습의 효율성이 낮았습니다. 연속함수로 활성함수를 변경하였고, Sigmoid함수는 대표적인 활성함수로 사용되게 되었다. 

 

두 번째, 상태가 2개인 경우에 한해서 인공 신경망의 마지막 Layer에 확률 값을 변환하는 역할로 사용된다(layer를 통과한 최종 결과를 변형한다). 이는 시그모이드 함수의 정의 자체가 Logit의 역변환이기 때문이다.

Softmax함수

softmax함수는 sigmoid함수의 일반적인 형태이다. 즉, 분류가 2개 이상인 경우 사용된다. 수식은 아래와 같다. 

soft max function

위의 식에서 $a_i$는 logit값이다. 

즉, softmax는 logit값을 확률로 다시 변경해준다. 

위의 수식 유도는 odds의 정의로 부터 유도 가능하다. 그 과정은 아래와 같다.

왜 e를 사용해야하는가?
logit이 마지막 layer로 오는 것은 정해져있기 때문에 e로 넣는 것이 계산에 용이하다

열심히 수식을 유도하다 보니 알아본 것인데, 사실은 볼츠만 인자와 볼츠만 통계에서 해당 수식을 가져다 썼다는 말도 있어서.. (1959년 Robert Duncan Luce는 자신의 책 Individual Choice Behavor: A Theoretical Analysis에서 
기계학습에 소프트맥스로 알려진 위 식을 사용할 것을 제안
하였다. 1989년 Hohn S. Bridle은 
비선형성 네트워크 출력을 확률로 처리하고자 소프트맥스 사용을 제안
하였다.)
관련 글이 적힌 블로그 링크를 첨부한다
https://toyourlight.tistory.com/16

유도 과정 1

(참고: https://velog.io/@gwkoo/logit-sigmoid-softmax%EC%9D%98-%EA%B4%80%EA%B3%84

https://opentutorials.org/module/3653/22995)

우리는 위의 식에서 X가 어떤 Class에 들어갈지 맞출 것이다. 이때 확률이 더 큰 쪽을 선택하는 것이다.

이를 Odds와 logit을 이용해 표현하면 다음과 같다(위의 유도 과정 참고)

• Classes: $C_1$, $C_2$
• Probiability of $C_1$ given $X$ = $P(C_1 \mid X)$
• Probiability of $C_2$ given $X$ = $P(C_2 \mid X)$

$$ odds = \frac{p}{1-p} = \frac{P(C_1 \mid X)}{1-P(C_1\mid X)}$$

$$ logits = ln(odds) = ln( \frac{p}{1-p} = ln(\frac{P(C_1 \mid X)}{1-P(C_1\mid X)})$$

이를 변형하면 우리는 output X에 관한 식을 얻는다(이진 분류임으로 Class 1의 여사건은 Class 2임)

$$\frac{p}{1-p} = \frac{P(C_1 \mid X)}{P(C_2 \ mid X)}= e^X$$ 

이를 k개의 클래스에 관해(해당 k class는 전체 class에서 i를 제외한 모든 class, 즉 $C_i^c = C_k$으로 가정한다, 즉 어떤 i가 오더라도 그것을 제외한 class들의 묶음이라고 하자, 그래서 이후 k-1개의 class까지 합한다) i의 class에 관한 식으로 일반화 하면 아래와 같다(i가 궁금한 사건) 

$$\begin{equation} \frac{p}{1-p} = \frac{P(C_i \mid X)}{P(C_k \mid X)}= e^X_i \label{eq1} \end{equation}$$

그럼 이를 i=1부터 K-1까지 더하면 

$$\sum\limits \frac{P(C_i \mid X)}{P(C_k \mid X)}= \sum\limits_{i=1}^{K-1}  e^X_i $$

위 식의 분모는 i에 관한 식이 아니기에 아래처럼 변경된다

$$\frac{P(C_1 \mid X)+ P(C_2 \mid X) + ... + P(C_k-1 \mid X) }{P(C_k \mid X)}=\sum\limits_{i=1}^{K-1}  e^X_i $$

그럼 확률의 총합이 1인것을 이용하면 아래와 같다

$$\frac{1- P(C_k \mid X) }{P(C_k \mid X) } = \sum\limits_{i=1}^{K-1}  e^X_i $$

그럼 이 식 중 k에 관한 부분을 i에 관한 식으로 변형하기 위해 (1)을 이용하고, (1)에 i 대신 k를 대입하면 $e^{z_k}=1$임으로 Softmax함수가 유도된다. 

최종 softmax식 유도

유도 과정 2(베이지안 관점에서 유도)

(참고: https://hyunlee103.tistory.com/12)

Logistic Function 유도

• Classes: $Y_1$, $Y_2$
• Probiability of $Y_1$ given $X$ = $P(Y_1 \mid X)$
• Probiability of $Y_2$ given $X$ = $P(Y_2 \mid X)$

위의 정의를 그대로 이용해보자(X는 Data이다)

참고로 $P(X \mid Y_i)$는 Likelihood가 된다(특정 class(Y) 분포에서 나온 데이터일 확률이기에)

각각의 Psosterior에 베이지안을 적용한 식은 아래와 같다

이 식을 통해 우리는 X의 분포가 동일하기에 각 Class에 관한 사후 확률을 우도와 Prior(Y)의 곱에 비례함을 알 수 있다.

그러면 k번째 class에 관한 우도와 Prior의 곱을 다음과 같이 $a_k$로 정의하자. 

그럼 다시 Class 1의 Posterior을 추정해보면 

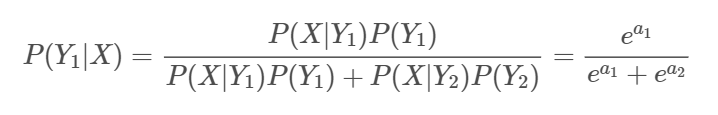
이다. 

이후 a에 관한 식을 Logit을 이용해 재정의하면

최종적으로 식이 Logistic Function이 된다. 

Softmax 유도

K개의 Class 중 Class 1에 대한 posteriror 추정으로 확장하면 Bayes Rule과 Law of total probability에 의해 아래 식이 유도된다. 

이를 다시 $a_k$에 관한 식으로 표현하면 우리가 아는 Softmax 식을 유도 가능하다.