[DB] Relational Algebra

본 글은 https://rebro.kr/146?category=484170 와 차제혁 교수님의 데이터베이스시스템및응용 수업을 기반으로 작성되었습니다. 

 

Relational Algebra는 SQL을 공부하기 전에 익히면 좋은 개념이다. SQL의 기본문법을 알아보기 전에 가볍게 정리해보자. 

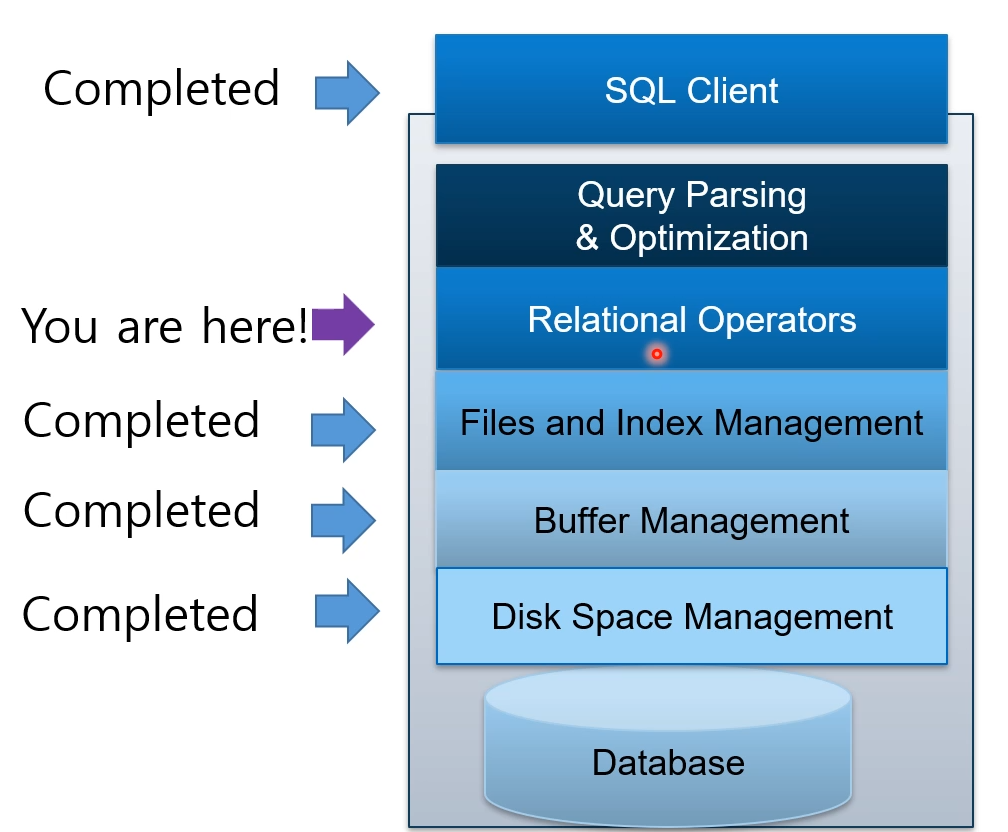
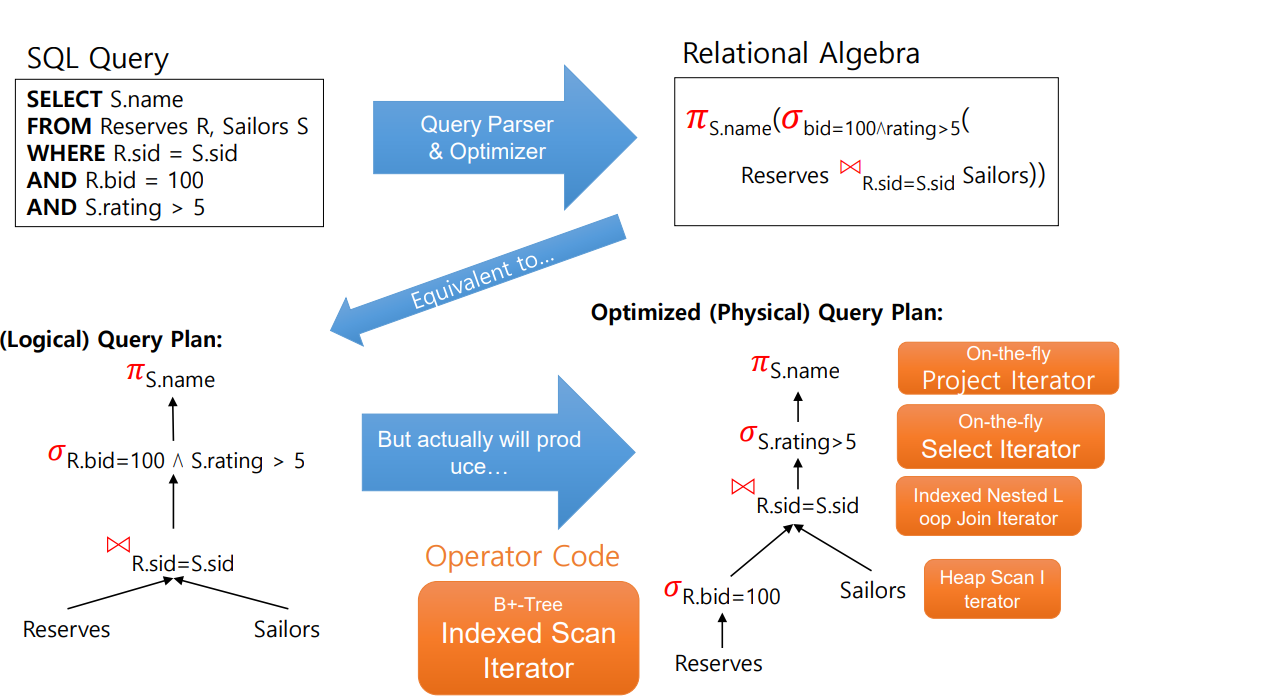
 Data Manipulation Languages(Relational algebra vs Relational Calculus)

데이터베이스로부터 정보를 얻거나, 저장하는데 사용하는 두 가지 주요 접근법이 있는데. 이는 절차적 언어와 비절차적 언어, 다시 말해 Relational Algebra와 Rleational calculus가 있다. 

 

Relational algebra(SQL의 기초, 절차적 언어):

연산자와 피연산자를 사용하여 수식 형태로 표현, 결과를 찾기 위한 데이터의 처리 과정을 구체화 함

기본 연산자: 선택(σ), 투영(π), 합집합(∪), 차집합(-), 카티션 곱(×) 등을 사용한다

 

Relational calculus(비절차적 언어):
수학적 논리와 술어 논리를 사용하여 표현. 원하는 결과를 구체화한다
튜플 변수와 논리 연산자를 사용

 

절차적 또는 비절차적 언어로 모든 쿼리를 기술할 수 있으면 데이터 언어를 관계적으로 완전(Relationally Complete)하다고 할 수 있다. 

Codd's Theroem에서는 관계대수와 관계 해석의 표현력이 동등하다는 것을 보이며(Declaritvbie represnttaion of queries와 Operational description을 연결), SQL을 관계 relational algebra로 compile할 수 있음을 보였다. 

 

Relational Algebra Overview

관계 대수에 관해 알아보자. 

관계대수, Relational Algebra는 절차적 언어로 릴레이션의 요소들에 적용되는 연산자이다. 이산수학의 집합이론에 기반한 relation에 관한 연산이다. 그럼으로 기본적으로 연산자는 set sementic을 따라 중복된 행을 제거한다. 

Relational Algebra 예시

Unary Operator

단항연산은 single relation에 관해서만 수행된다. 

projection은 주어진 속성들만 포함하는 릴레이션을 반환, 중복되는 원소가 있으면 중복을 제거 

selection은 릴레이션에서 조건을 만족하는 tuple(전체)를 추출해주는 연산자

renaming은 속성명을 재정의힌다

Binary Operators: pairs of relations

Union과 set-difference는 각각 합집합과 차집합과 유사하다. 

Cross-product는 Cartiesian product로 두 릴레이션의 튜플로 구성가능한 모든 조합을 생성(둘 중 하나만 있어도)

 

Detail Relational operator

 

Projection: πA1,A2,...,An(R)

Sql의 SELECT list와 대응된다. 특정 columns(vertical selction)의 subset을 가져온다. 중복죄는 원소가 생기면 중복을 제거하고 보여준다. 

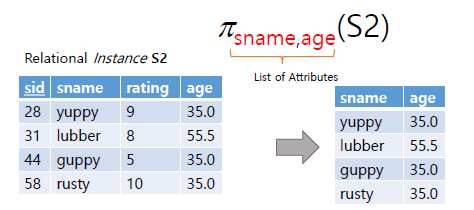
위의 예시 student 릴레이션에 적용하면 다음과 같다(set sementic이기에 중복된 행을 허용하지 않는다)

ex: πGrade,Major(student)

다만, 실제 시스템은 자동으로 중복을 제거하지 않는다. 예를 들어 SQL에서 Select Distinct를 명시적으로 사용하지 않는한, 동일한 열 값이 중복되어도 그대로 출력된다. 

이는 성능측면에서 매우 비용이 많이 들며 또한 데이터 sementic(의미)에서 왜곡이 발생할 수도 있다. 예를 들어 한 학생이 같은 과목을 여러번 수강할 수 있으면 중복된 데이터도 의미를 가진다. 

Select: σ predicate(R) _ sigma

SQL에서 WHERE에 해당한다. Output schmea와 input이 동일하고, 중복을 제거하지 않는다.

Select operation은 릴레이션(R)에서 조건(predicate)을 만족하는 subset of row(horizontal, 행단위로 뽑음)을 추출해준다. 

조건들(predicate)은 and, or, not 등을 이용해 보다 복잡하게 구성 가능하다. 

 

ex: composing select and project

sailor의 이름이 필요하고, 그 sailor는 rating > 8이상이어야한다. 

 

이에 맞게 하려면 sigma연산으로 rating조건을 뽑고(행으로) 이후 파이로 name만 선택하면 된다. 

파이를 먼저 쓰면 rating정보가 없기에 연산이 이루어지지 않는다. 즉 Selection 연산은 필요한 열에 의존하므로, 먼저 데이터를 필터링한 후 해당 열을 제거하는 것이 올바른 순서이다. 

 

Union: R ∪ S

Union 연산은 두개의 서로 다른 input relation 을 요구하고 두 릴레이션의 합집합을 반환한다. SQL 연산자도 UNION이다. 

입력으로 들어오는 두 릴레이션은 속성(attirbute의 개수가 같고), 대응되는 필드들이 동일한 domain을 가지고 있어야한다. 

(Fields in correspondingpositionshave same type)

 

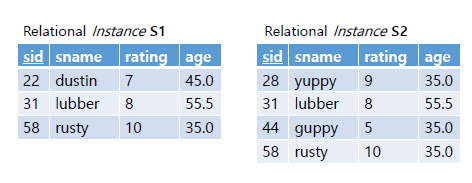
중복 처리의 경우 Union연산에서는 set sementic을 따라 중복된 행은 제거된다. 만일 UNION ALL을 사용하면 중복된 행을 사용가능하다. 앞서 말햇듯, 중복제거는 비용이 많이 드는 작업이기에 불필요한 경우 UNION ALL을 사용하는 것이 좋다.

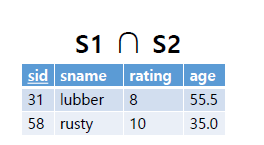
Compound: Intersection S1 ∩ Se

SQL로는 INTERSECT로 표현하며 union과 동일하게 두 relation은 compatible해야하며, SQL에서는 All 옵션을 가진다.

또한 아래의 Difference operator로도 intersection을 표현가능하다. S1 —(S1 —S2)

 

Set Difference: R - S

SQL에서는 EXCEPT로 사용되는 Difference는 Union과 동일하게 compatible해야한다(속성이 같고 대응 필드가 동일한 도메인을 가짐). 차집합을 반환하고 R에 속해있지만 S에는 속해있지 않은 튜플의 집합이다. 

Uinon과 동일하게 EXCEPT ALL이 존재하며 이를 통해 Duplicate의 허용여부를 결정가능하다(SQL에서는!)

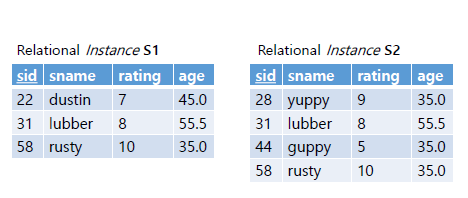
Cross-Product (×)

Cross Product, R X S는 each row of R와 S의 row로 가능한 모든 가능한 조합을 뽑아낸다. 최대 R과 S의 Cardinalty의 곱의 개수가 존재가능하다. Compatiblity를 만족할 필요 없고, Duplicate한 경우는 생성되지 않는다(만일 R과 S에 공통 속성이 있는 경우 둘 중 하나의 이름을 재정의해야한다고 한다)

Renaming ( 𝜌= “rho” )

Renaming은 relation과 attribute을 재명명하는 연산자이다. 하지만 다른 relational 연산자의 경우 이름을 보통 필요로 하지 않는 다는 것을 기억하자. 

 

Theta Join (⋈𝜃) and Natural Join (⋈)

Join 연산은 두개의 테이블을 결합하는 연산으로, 두 릴레이션 R, S의 공통 속성에 대해 조건에 맞는 행을 연결한다.

𝜎𝜃( R ×S)으로도 표현 가능할 것이다. 즉  공동속성으로 가능한 조합 중 원하는 속성을 뽑는 형태이다. 

Theta Join: 논리적 표현식을 사용한 조인(두 테이블의 속성간의 관계를 정의)/중복 유지

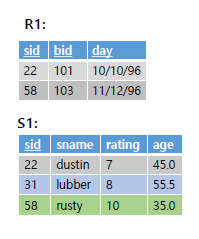
아래의 예시를 보면 sid를 공통속성으로 하여 결합하는 것을 확인 가능하다(겹치는 22, 58만 가져옴) 또한, sid열이 동일한 이름으로 두번 포함되어있기에 rename이 필요함을 확인가능하다. 

SELECT * 
FROM sailors S, boats B
WHERE S.sid = B.sid AND B.color = 'red';

 

아래의 예시를 보고 더 나이가 많은 선원을 찾는 조인을 수행해보자.

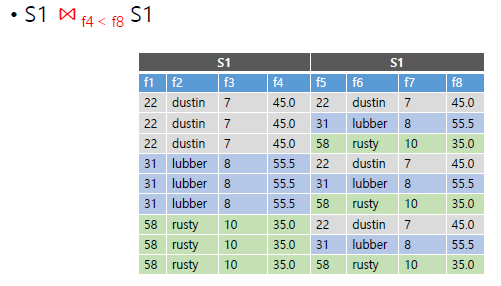
우선 

두 개의 동일한 테이블 S1을 f4(나이) < f8(나이) 조건으로 조인. 즉 연장자 sailor를 찾는다. 

우측 이미지는 age < ag2를 비교 

 

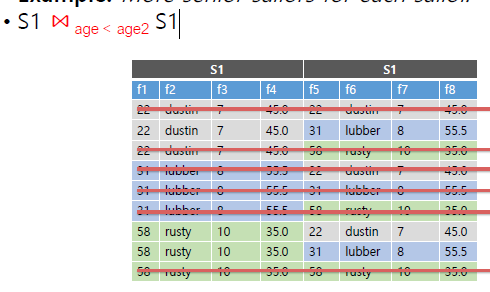
최종적으로 아래와 같이 결과가 정리된다.

Natural Join: 동일한 이름의 컬럼을 기준으로 두 테이블을 조인(Eqi join = 함). 중복된 결과를 제거 

Equi join, 즉 theta join이 =연산자인 경우를 의미하고, 동일한 이름의 컬럼을 기준으로 Equi join을 실행하고 중복된 열을 제거하는 연산자. 풀어쓰면 아래와 같을 것이다. 

SELECT * 
FROM sailors NATURAL JOIN boats;

 

예시 그림을 보면 아래와 같다. 

Division ( R / S)

릴레이션 S의 모든 tuple과 관련이 있는 릴레이션 R의 tuple을 반환하는 관계대수이다. 

 

 

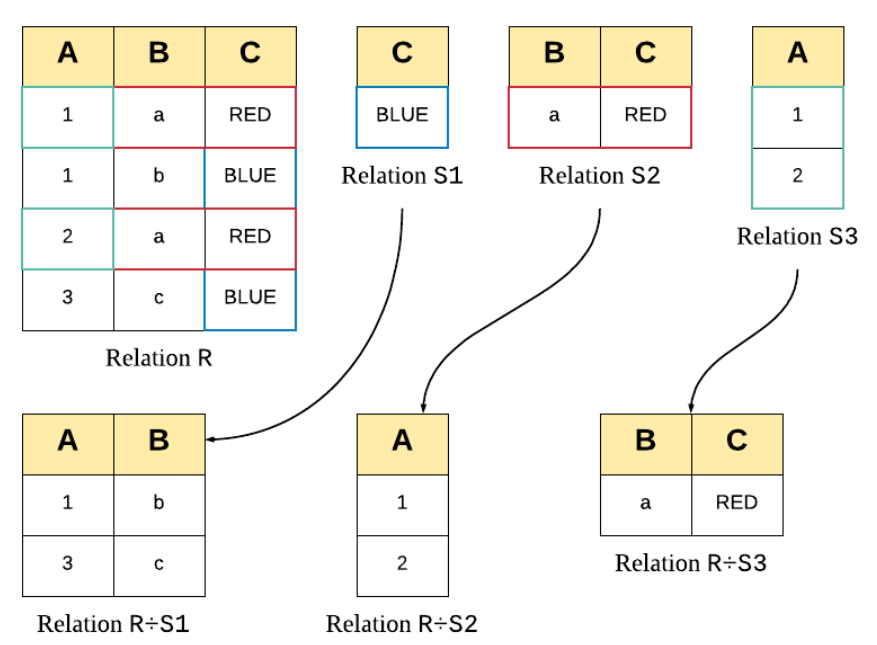
Divison 연산을 풀어쓰면 아래와 같다. 

우선 위의 A/B는 단계적으로 다음과 같이 구현 가능하다. 

Step1: A x만 고르고 에서 B와 cross-product한다. 

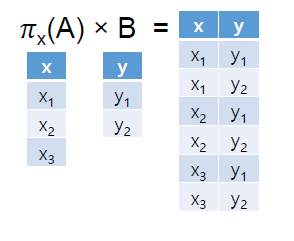
step2: 이후 A를 차집합한다. 이는 그러면 A와 비교하여 A에는 없는 X의 value만 남는다. 

 

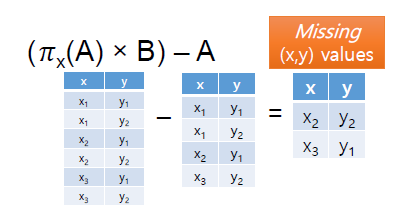
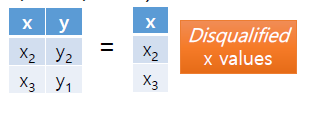
그럼으로 이를 빼주면 A에서 B의 값이 존재하는 즉 /에 해당하는 수식만 남는다. 최종적으로 아래와 같다.

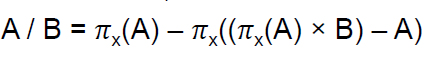
Division 연산의 의미는, A에 있는 모든 x 값이 B에 있는 모든 y 값과 매핑되는 경우에만 결과에 포함된다는 것이다.