-
[Boosting] AdaBoost, AdaCost, AUC-Based Boosting전공&대외활동 이야기 2025. 3. 16. 19:32
Boosting

Boosting알고리즘은 Classification에서 널리 쓰이던 방법이나 다른 예측 모형에도 사용 가능하다. Boosting은 "weak classifer"의 결과를 결합시켜 하나의 powerful commitee를 만드는 방법이다. 순차적 알고리즘이라고 생각하면 된다.
Adaptive Boosting(AdaBoost)

위의 그림 예시처럼 Adaboost는 기존의 weak learner가 잘 구분하지 못했던 부분을 하나씩 매꾸면서 더 잘 구분해가는 모습을 볼 수 있다. Pseudo Code를 보면서 더 알아보자.

우선 첫줄에서 볼 수 있듯이 각 데이터 샘플에 동일한 가중치를 부여한다.

이후 t=1 부터 T까지 가중치 분포를 고려하여 weak classifer를 학습시킨다.
이때, 해당 분류모델의 가중치 αt는 다음과 같이 계산된다.

수식을 보면 이는 분자에 올바르게 분류된 샘플의 가중치 합, 분모에 잘못 분류된 샘플의 가중치 합을 가지는 로그비이다.
이는 항상 양수여야 하며, 성능이 약한 분류기는 작은 값(올바르게 분류된 샘플이 분자)를 성능이 좋은 분류는 큰 값을 가지도록 설계되어있다. 항상 양수여야한다는 의미는 결국 log 안에 값이 1보다 큰 값, 즉 랜덤분류기보다는 모두 좋은 성능을 가지는 분류기일 것이다라는 가정이 깔려있다.

이제 D는 위에서 계산된 분류기의 성능에 따른 at를 이용하여 샘플에 가중치를 부과한다.
만일 샘플이 올바르게 분류된 경우(즉 y와 h의 부호가 같음)는 exp(-at)로 작은 가중치를 부여받고
반대로 잘못 분류된 경우는 가중치가 증가한다.
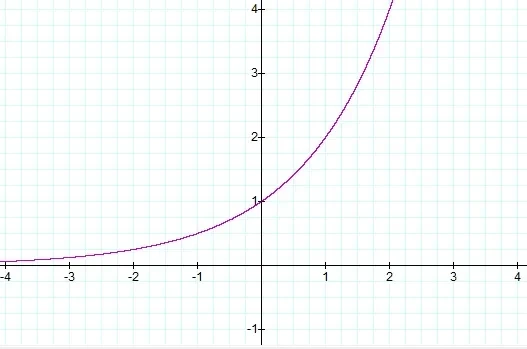
지수함수 마지막으로 z는 정규화 상수로 붙는다. 즉 모든 D의 총합은 1이다.
최종적으로 모든 분류기들의 가중합을 계산하고(잘 맞추면 더 많이 반영) 이를 이용해 최종 클래스를 결정한다.
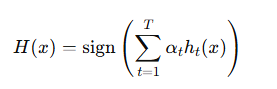
Example
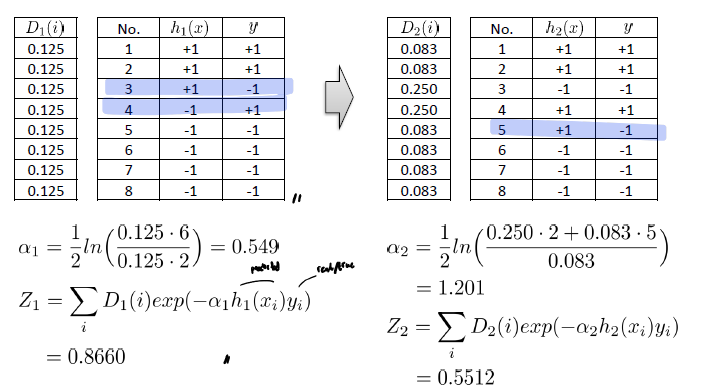
Example을 보면 t=1에서 잘못 분류된 값이 2개이기 때문에 a1의 분모에 2가 있는 것을 확인가능하고,
이를 이용해 z를 계산하고 D2가 업데이트 된 모습을 확인 가능하다. 또한 틀린 부분의 D2의 값이 증가했음을 확인 가능하다.
Theoretical Analysis of Adaboost
AdaBoost as a minimizer of an upper bound on the empirical error. 즉, 경험적 오류의 상한을 최소화하는 문제를 풀고 있다.
Empircal Error는 아래와 같이 수식으로 표현된다. 즉, 잘못 예측된 샘플의 비율이다(I, Indicator function)
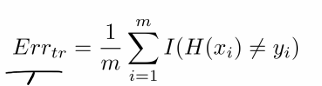
우선 아래의 수식이 성립한다.

이는 잘못분류된 경우 I()는 1이고, exp() 수식은 1보다 크거나 같다. 올바르게 분류된 경우 I는 0이고, exp 수식은 0보다 크다. 즉, 모든 경우 exp가 항상 크기 때문에 성립한다.
이제 우리는 exp() 수식이 Zt의 곱들과 같음을 보여야한다.
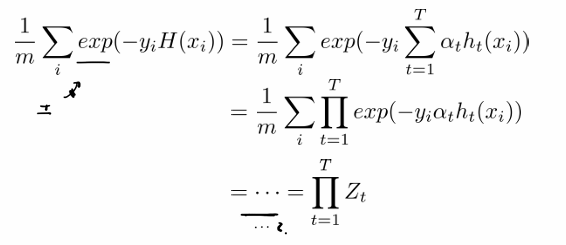
이를 보이기 위해

exp 수식에서 a를 하나씩 풀어서 쓰면 최종적으로 아래와 같이 보일 수 있다.
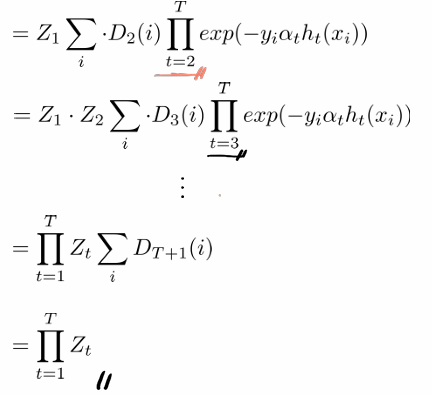
이를 통해 at를 고르는 것은 Zt를 greedly minmizing하는 것을 알 수 있다.
AdaCost: Cost-Sensitive Boosting
AdaCost는 costly wrong classification, 틀렸을 때 더 치명적인 부분의 가중치를 더 공격적으로 증가시키고, 비용이 많이 드는 올바른 분류의 가중치는 천천히 감소시키는, Cost-Sensitive Boosting 기법이다.
아래의 Confustion matrx를 보면 일반적으로 C(+, -), 즉 양성인데 양성이 아니라고 판단한 FN의 가중치를 더 크게 줘야함을 알 수 있다.
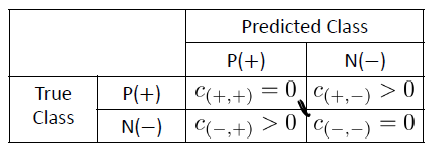

간단히 이를 생각해보면, 제품을 생산하는 입장에서는 불량률을 줄이는게 더 중요하다~ 라는 의미이다.
이제 아래의 코드를 보면 AdaBoot와 다른 점이 존재한다.

1. 초기화가 균등하게 이루어지 지지않고, 각 샘플별 cost에 따라 매겨진다.2. at 또한 B라는 비용조정함수가(Cost adjustment factor) 붙어있다. 이를 통해
- 비용이 높은 샘플(β(i) 큰 샘플)의 경우, 가중치가 더욱 증가 → 다음 반복에서 더 중요한 샘플로 반영됨.
- 비용이 낮은 샘플(β(i)값이 작은 샘플)의 경우, 가중치 증가가 적음 → 덜 중요한 샘플로 반영됨.
의 효과를 누린다.

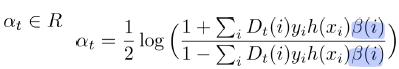
조금 더 자세한 설명은 아래의 슬라이드를 보자.

즉 비용 조정함수는 샘플이 올바르게 분류된 경우 B+ 를 아닌 경우 B-를 부여하며 B- 즉 오분류 샘플의 비용조정함수는 비용 c가 증가할 수록 같이 증가하는 non-decreasing function이며, 반대로 올바르게 분류된 샘플의 경우 반대로 비용이 증가할 수록 감소해야하는 non-increasing sample이다. 올바르게 분류된 샘플의 비용이 클수록 감소시키는 이유는 이미 잘 학습된 샘플에 관해서는 중요도를 줄이기 위함이다.
Theoretical Analysis

이제 다음을 목표로 증명을 해보자. 이는 cumulative missclasification error의 합이 정규화 상수들의 곱 * 모든 샘플의 비용총합에 의해 결정됨을 보이고자하는 것이다. 즉, Zt 를 최소화하면 최종적으로 학습 오류도 줄일 수 있음을 증명하는 과정.
이는 아래의 과정을 통해 증명된다.
우선 다음이 성립합을 보이자.
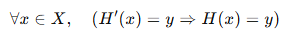
이는 중간 분류기 H'(x)가 올바르게 예측된다면 최종 분류기 또한 올바르게 예측이 된다는 의미이다.
아래의 증명과정을 통해 증명이 가능하다.
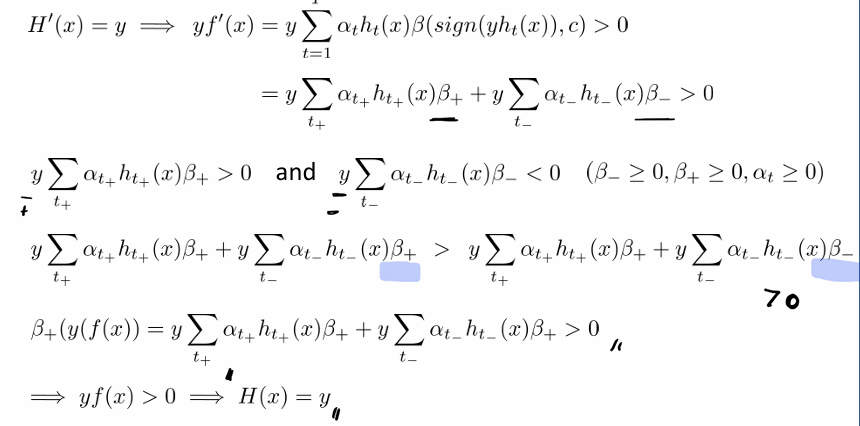
증명과정을 간단히 보면 올바른 예측을 한 경우와 올바르지 못하게 예측한 경우로 나누어서 증명을 보임을 알 수 있다.
이후 아래를 증명하면

아래의 과정을 거쳐 증명가능하다.


AdaAUC
이제 마지막으로 AdaAUC에 관해 알아보자.
이는 AUC 자체를 학습목표로 삼아 이를 maximize하는 알고리즘이다. 그럼 역으로 1-AUC를 minimize하면 된다.
그럼 어떻게 at를 정의하고 구할까?
Theoretical Analysis
h()를 weak classifier라고 하고 at는 그의 weight라고 하자.
우리는 H(), Storng classifer 하에서 1-AUC의 상한이 다음과 같음을 보일 수 있다.

이는 1-AUC가 지수 손실 함수의 평균보다 크지 않음을 보인다.
이를 통해 초기 가중치에 관해 at는 다음과 같이 업데이트가 됨을 확인 가능하다.

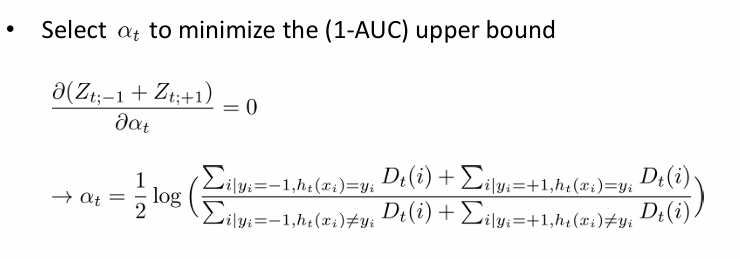
그럼으로 최종적으로 알고리즘은 아래와 같이 작성된다.

초기 가중치는 양성 및 음성 샘플의 개수 차이를 고려하여 각각 가중치를 초기화한다.
이후 t=1~T까지 계산하며 최적화를 하는 가정을 거친다.
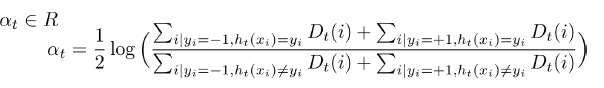
'전공&대외활동 이야기' 카테고리의 다른 글
[TIL][Imbalanced Data] Stratified Random Sampling, SMOTE (0) 2025.03.16