[Time Series][Change point Detection] CUSUM method

CUSUM에 관한 내용을 최근 읽었던 논문에서 기초하고 있는 방법인만큼 해당 내용을 보다 상세히 작성하여보았다. 
대부분은 https://zephyrus1111.tistory.com/400 에서 기초하여 작성함을 밝힌다 

 

출처: https://nado-coding.tistory.com/13

 

- 문제정의 

CUSUM 알고리즘이 풀고자하는 문제는 시계열내에 급격한 변경점이 없다는 귀무가설(H0)과 하나의 변경점이 있다는 대립가설 Ha을 세우고 이 중 어떤것을 선택해야하는지에 관한 문제이다. 

 

먼저 시계열 데이터 Xt가 있다고 하자(t는 1부터 k까지 존재), 각가은 IID 조건을 따르고 해당 확률분포의 확률밀도함수를 p(x)라 하자. 

Change point dection은 시계열 데이터에서 변화가 생겼을 경우에 해당하는 시점 tc를 찾는 알고리즘이기에 θ(확률함수의 모수)를 변화 시점 전과 후로 다르게 설정한다. 

 

그럼으로 시계열 내의 급격한 변화가 없다는 H0 가정하에서는 

 

하나의 급격한 변화시점이 있다는 대립가설 Ha 아래에서는 

가 성립함을 알 수 있다(확률의 각 사건이 독립임을 가정함으로)

 

 

- Basic Formula for cusum 

 

식을 보면 알 수 있듯이 S는 cumulative sum, 즉 누적합을 의미한다. 해당 값 S가 특정 임계값 h 이상이라면 변화가 있다고 감지한다(min인 경우 감소방향 변화도 찾을 수 있음)

 

w는 paper에서 특정값을 언급하지는 않음. 다만, 대다수의 경우liklihood를 사용하고 아닌 경우도 있다. 

 

결국 특정 기준값과 실제값 간의 차이를 누적하여 임계값을 초과하는 시점을 Change point로 하는 알고리즘을 모두 CUSUM 계열이라고 한다. 

 

 

 

 

Log Likelihood Ratio Based CUSUM의  증명 및 전개과정

 

이제 log likelihood ration cusum에 관해 우선 정리해보자. 

- 가설 선택

CUSUM 알고리즘은 그럼 두 가설 중 어떤것을 선택해야하는가?

 

일반적으로 CUSUM 알고리즘은 개별 로그 우도비(Log Likelihood Ratio)의 누적합을 이용하여 해당 누적합이 사용자가 지정한 상한선을 넘어갔을 경우 변경점이 존재한다고 말하는 알고리즘이다. 

 

우선 우리는 각 가설 하에 확률밀도함수를 알고 있다면(물론 실제 응용에서는 확률분포를 알기 어려운 경우가 많음으로 Semi-parametric방법을 이용하여 score function으로 이를 대체하기도 함), Likelihood Function 또한 알 수 있고, 이에 따라 당연히 Log-liklihood Funtion도 알 수 있다. 그럼으로 Log Likelihood Ratio도 알 수 있다. 이는 다음과 같다. 

 

우리는 이 LLR이 크면 클수록(1에서 멀수록이라고 하) 대립가설 Ha를 지지하게 된다 (통계적 유의, 우도비 검정, 정확히는 귀무가설을 기각)

이제 이 LLR을 (1), (2) 수식을 이용하여 표현하면 아래와 같이 표현된다(tc 시점까지의 θ0 모수를 가지는 확률곱은 지워지고, 이후 부분인 tc부터 K까지 부분만 남음) 

 

-  θ(확률함수의 모수)를 아는 경우

   θ를 알고있다고 하더라도 LLR을 계산할 수는 없다. 그 이유는 우리는 tc, 즉 변화점을 알아야 식 (1)과 식(2)를(정확히는 식 2) 계산 가능하기 때문이다. 이때 Kay는 Generalized Likelihood Ratio Test를 제안하였다. 

바로 tc를 모든 시간 1에서 k까지 관하여로 가정하여 각각 LLR을 모두 계산한 뒤 이 중 최대값을 검정통계량(or 표본통계)으로 하는 것이다.이를 수식으로 나타내면 아래와 같다. 

 

그럼 이 G(k)가 우리가 설정한 상한선인 h를 넘어가는 경우에 귀무가설을 기각한다. 이때 G(k)를 decision function, 의사결정 함수라고 한다(일반화 우도비라고도 한다고함). 

- change point 추정

변경 시점인 t를 추정하는 것은 위에서 LLR을 통해 변경시점이 있다!라고 판정된, 즉 G(k) > h인 경우 이를 만족하는 최초의 k를 k'이라고 하자(시계열 데이터의 관측길이). 이때 아래 수식과 같이 변경시점은 해당 k지점까지 있었던 시점들중 LLR을 가장 크게하는 시점을 변경시점으로 한다. 

 

의사결정 함수 

앞서 말한 것처럼 의사결정함수는 1~k point에서 LLR의 max를 취한 함수였다. 

의사결정함수는 아래와 같이 다른 방식으로도 살펴볼 수 있다. 

 

a. 일반형 

s(n)을 우선 아래와 같이 정의하자. 

이를 개별 로그 우도비(Instantaneous Log Likelihood Ratio)라고 한다. 

 

s의 1부터 k까지의 누적합(cumlative sum of LLR) S(k)는 그럼 아래와 같을 것이다. 

누적합을 이용하여 (4), k시점까지의 LLR을 표현하면

(9)와 같다(k 끝 지점까지의 누적합 - tc까지의 누적합은 당연히 그 중간부분임)

그럼 구한 (9)를 의사결정함수, argmax 수식인 (5), (6)에 적용하면 아래를 알 수 있다. 

(5) 식은 max 식인데 S(k)는 상수임으로 변하는 값인 S(tc)가 min일 때 최소이다. 그럼으로 10 성립

 

(11)의 경우도 (10)과 같이 argmax가 argmin식으로 변경된 것임.

 

이때 k'의 경우 inf{k: G(k) > h}를 표현한 것이다. 

여기서 알 수 있는 것은 앞에서 살펴본 변경점 존재 여부를 나타내는 알고리즘은 개별 로그 우도비의 누적합으로 표현될 수 있다는 것이며 문자 그대로 CUSUM은 누적합으로부터 알고리즘이 도출되었음을 의미한다. 

 

위 식에서 유도된 G(K) = S(k) - m(k)를 일반형이라고 한다(앞서 말한것처럼 S(k)는 k(관측끝)까지의 누적합, m(k)는 1~change point까지의 min값이다).

 

개별 로그 우도비 누적합과 변경점 존재 여부와의 관련성은 아래와 같다. 이때 θ는 알고있다고 가정하자. 

만일 변경점이 없는 상태가 유지되는 경우는 확률밀도함수가 변하지 않고 θ0의 모수를 가지는 확률밀도함수일 것이다. 

그렇게 되면 개별 로그 우도비 s(t)는 음수를 유지함으로  t시점까지의 누적합 S(t)는 계속 감소할 것이다. 

왜 개별 로그 우도는 음수일까? 
변경점이 없다는 가정 하에서는 데이터가 여전히 기존 분포를 따르게 된다. 이 경우 새로운 데이터에 관해 
p(xt​∣θ0​))> p(xt​∣θ1​) 임으로(기존 분포를 따를 확률이 높음) 따라서 log 안의 값은 1보다 작고 이는 곧 로그 우도비가 음수임을 의미한다.  

출처: https://zephyrus1111.tistory.com/400

 

하지만 특정 변경점이 있다면 해당 변경점 이후부터는 X의 확률밀도함수가 θ1에 해당하는 함수로 바뀌게 됨으로 개별 로그 우도비 s(t)는 양수로 전환된다. 이때부터는 S(t)가 커지게 된다. 

출처: https://zephyrus1111.tistory.com/400

 

하지만 이런 한번의 S(t)의 방향성의 변화가 곧 완전히 분포가 바뀌었다와 동치라고 말할 수는 없을 것이다. 

즉, 이러한 현상의 지속성, 로그 우도비가 양수인 상태가 어느정도로 지속되어야 변경점이 있다고 할 수 있을 것이다. 

CUSUM 알고리즘에서는 S(t)가 m(t)+h 보다 커지는 경우에 변경점이 있다고 판단한다. 

앞서 살펴보았듯, m(t)는 min(1~t)이다. 아래의 그림을 보면 m(t) 즉 가장 최저점일 때 + h인 값이
S(t), t까지의 누적합보다 작은 경우(반대로 S(t)가 큰 경우) 변경점이 있다고 판단한다.
이는 t까지의 누적합 S(t)는 변경점이 없을 경우 계속 음의 값을 지님으로 G(t)는 분포가 변화한 시점부터 현재 t시점까지의 log 우도비 값의 합이며 이것이 h라는 사용자가 정한 상한을 넘어가는 순간 변경이 있다고 하는 알고리즘임을 알 수 있다. 

 

이때 주의해야할 것은 변경점이 있다고 안 시점 이전에 변경점이 존재한다는 것이다. 이는 변경점은 첫 시점부터 t시점 사이에서 S(t)가 최소가 되는 지점을 말하기 때문이다. 

b. 재귀형(Recursive form)

대다수의 CUSUM 알고리즘 설명은  재귀형으로 표현하고는 한다. 이는 일반형의 경우 실시간으로 변경점을 알 수 없기 대문이다(처음부터 현재 시점까지의 값을 비교한 뒤 최소값을 찾아야함)

따라서 위와 같은 재귀형이 사용되고는 한다. 

 

이런 경우 이전값에다가 현재의 개별 로그 우도비만 더해주면 되기에 실시간 업데이트가 가능하다. 

해당 재귀식의 유도 및 증명은 아래의 이미지를 참고하자(출처는 동일 블로그글)

 

 

정규분포

 

만일 시계열 X가 독립인 정규분포를 따른다고 하고,  change point 이전에는 평균이 u0, 이후에는 u1으로 변경되었고 표준편차는
σ로 동일하다고 하자. 그럼 확률 밀도함수는 아래와 같이 정의된다. 

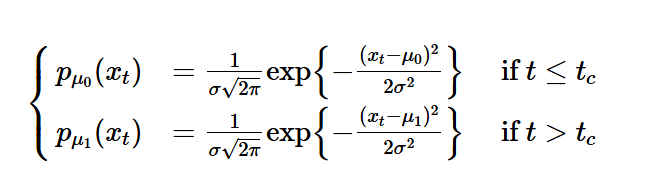
이를 이용한 개별로그 우도비 s(t)는 아래와 같다.

모수를 모르는 상황

앞서서까지는 모수를 모두 안다고 가정하였지만, 실제로는 알 수 없는 경우가 대다수일 것이다. 따라서 데이터를 이용한 추정값을 이용해야한다. 

정규분포를 예제로 하자(표본평균 이용한 추정). 아래의 관계가 성립할때를 가정하자. 

이때 σ를 지정해준다고 하면, u0의 추정에 따라 u1은 추정된다. 고로 다음과 같은 식이 성립함을 쉽게 알 수 있다. 

 

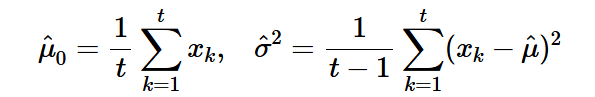
그럼 h는 어떻게 추정가능한가?

h는 일반화 우도비를 시간에 따라서 그려본 뒤 설정할 수 있다. 이때 h를 작게 설정하면 아주 작은 변화를 탐지하며 크게 설정하면 작은 변화는 무시하고 크게 변하는 지점을 설정할 수 있다고 한다(자세한건 향후 논문을 읽어가며 보충 예정)

 

최종 정리: CUSUM 알고리즘

1. 초기화 단계
초기 CUSUM 값 설정: S₀ = 0 목표값(μ₀), 민감도 매개변수(k, 변화의 크기), 임계값(h) 설정
2. 데이터 수집
시계열 데이터 x₁, x₂, ..., xₙ 관측
3. LLR(Log-Likelihood Ratio) 계산 및 CUSUM 통계량 계산
각 시점에서 로그 우도비 계산한. LLR은 변화 전후 확률 분포의 비율을 로그 변환한 값을 의미한다. 만일 정규분포라면 아래와 같을 것이다. 

 

이때 위의 식은 u0를 기준으로 커지는 지점만 찾거나 작아지는 지점만 찾는 one-sided CUSUM알고리즘이다(단방향 알고리즘)

 

Two-side의 경우 아래의 두 s값을 이용한다(u1이 u0보다 각각 큰 경우 작은 경우

 

4. 변화점 탐지 및 변화점 위치 추정
CUSUM 통계량, G(t) > h라면  임계값 h를 초과하는지 확인 초과하는 경우 변화점으로 판단

5. 알고리즘 반복
새로운 데이터 포인트가 들어올 때마다 3-6단계 반복

 

CUSUM알고리즘은 우도함수가 존재하고, 또 해당 가정한 우도함수 즉 확률분포가 맞다면 잘 작동하는 알고리즘이지만, h를 잘 선택해야한다는 단점 또한 존재한다. 

이어지는 논문들을 읽으며 해당부분을 어떻게 극복하려고 했는지 작성해보겠다.