[Kernel][미완] Reproducing Kernel Hilbert Space (RKHS)

[아직 미완... 한번 더 내용을 정리해서 올릴 예정임]

 

Kernel에 관하여 우선 간단히 정리하고 이후에 RKHS 커널에 관해서 자세히 알아보자. 

 

커널은 우선 SVM과 같은 알고리즘에서 중요한 역할을 하는 함수로, 데이터를 고차원 Feature map으로 맵핑시켜서 선형분할 가능하게 만들어준다.

추가 참고자료: http://www.gatsby.ucl.ac.uk/~gretton/coursefiles/lecture4_introToRKHS.pdf
대부분의 Lemma의 참고자료 

 

좌: 필자의 인공지능 수업 필기에서 내용 발최 우:  http://www.gatsby.ucl.ac.uk/~gretton/coursefiles/lecture4_introToRKHS.pdf

 

Kernel

저차원 입력 데이터를 고차원 특징 공간으로 매핑하여, 저차원에서는 보지 못했던, 학습하지 못했던 패턴을 파악하도록하는 함수이다. 

다시 말해 비선형 데이터를 고차원에 맵핑시켜 선형적으로도 학습 가능하게 한 것이다. 이는 Cover's Theorem에 근간하고 있다. 

이는 고차원 공간, 즉 d가 커지면 커질 수록 선형 분리 가능성이 증가함을 말한다. 이는 각 점이 가능한한 독립적이어야한다는 가정을 가진다. 

Let the number of homogeneously linearly separable sets of N points in d dimensions be defined as a 
counting function C(N,d) of the number of points  N and the dimensionality d
The theorem states that

 

 

 

그럼 이제 Ø를 저차원에서 고차원으로 mapping해주는 mapping function이라고 하자. 

우리가 만일 Ø(x) , Ø(y)를 내적하려고 할때, 이들을 맵핑하고 내적을 계하게 되면 그 계산량이 너무 커진다는 단점이 있다.

이를 해결해주는 것이 바로 Kernel Trick이다. 

 

Kernel Trick

 

위의 예시를 잘 보자, 우리가 만일 x1, x2 두개의 데이터를 위에서 정의한 고차원 맵핑함수 Ø에 넣고 이 둘을 내적한다고 하면 

1. 맵핑함수의 결과뽑기

2. 내적 계산

이렇게 2단계를 거쳐야한다. 하지만 수식의 끝에서 볼 수 있듯이 이는 단순히 두 input인 x와 y의 내적의 제곱을 수행하는 것으로 간단히 수행가능하기도 하다.   고차원 변환을 수행하지 않고도 변환된 공간에서의 내적 값을 커널 함수로 바로 계산할 수 있게 해주는 것이 Kernel Trick이다. 

 

이는 언제나 가능할까? 또 K(), 즉 커널은 무엇인가? 이에 답해주는 것이 Mercer's  Theorem이다. 

Mercer's  Theorem

 

K(Xi, ... Xj) is Positive Definte Kernel then,
There is at least one Ø(x), such that Ø(xi)^T Ø(xj) = K(xi, xj)

 

 

Mercer's Therem에 따라 우리는 Kernel trick을 매우 쉽게 사용 가능하다!

 

물론 객체를 잘 선택된 특징을 통해 분류하는 것은 ML에서 매우 일반적인 접근방법이나, 커널 기반 방법들은 무한히 많은 특징들을 활용할 수 있다는 점이다. 이는 learning algorithms이 특징들간의 내적으로 정의될 경우(유사도 개념) 가능하며, 이러한 내적을 closed form으로 계산 할 수 있을 때 성립한다. 

 

Back to Kernel... 

우선 그러면 내적을 통해 힐베르트 공간을 정의하자. 

 

위의 Def 1에 따르면 H라는 vector space에 대한 내적은 linearity, symmetry, postive difinite 조건을 만족할 때 내적이라 할 수 있다. 그럼 우리는 H에서 norm을 내적으로 정의할 수 있다. 

 

이제 우리는 내적이 정의된 공간이며, 추가적인 기술적 조건을 만족하는 공간을 힐베르트 공간(Hilbert space) 이라고 한다.

벡터 공간(Vector Space): 벡터 덧셈과 스칼라 곱셈이 가능함.
내적 공간(Inner Product Space): 내적(inner product, 점곱)이 정의됨.
완비성(Completeness): 모든 코시 수열(Cauchy sequence)이 그 공간에서 수렴해야 함.
무한 차원 가능: 보통 무한 차원의 공간을 다룸.

 

 

이제 Def 3에 따라서  우리는 어떤 R-Hilbert 공간 H가 존재하고 이 H에 X를 mapping하는 함수 Ø가 존재할 때, 우리는 Kernel을 정의할 수 있다. 

 

X에 대한 조건은 거의 없다, 즉 원소들 사이의 관한 내적이 직접 정의될 필요는 없다.

예를 들어, 문서(document)들을 생각해보자. 두 개의 책(book) 자체에 대해 내적을 정의할 수는 없지만, 책의 텍스트에서 추출한 특징(feature) 들에 대해서는 내적을 정의할 수 있다.

 

Kernel의 특성

앞서 말한 힐베르트 공간에 관해서 우리는 내적이 가능한 공간이라는 것과 벡터 공간이라는 것을 보였다. 

그럼 Completeness(완비성)란 무엇일까? 

 

우선 코시 수열(Cauchy sequence)를 알아보자. 

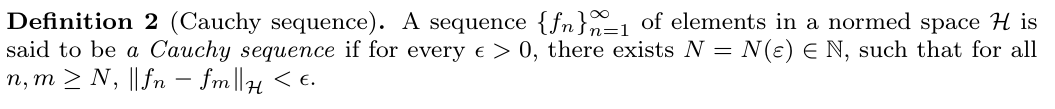
In mathematics, a Cauchy sequence is a sequence whose elements become arbitrarily close to each other as the sequence progresses

 

위의 Def2 에따라, 코시 수열은 수열들의 항(fm, fn)들이 서로 가까워지는 수열을 의미한다. 즉 어떤 숫자에 가까워지는 수열을 의미

이제 Completeness란 모든 코시 수열이 해당 공간 내에서 수렴함을 의미한다. 

 

Completeness(완비성): 실수의 성질, 빈틈이 없다 
R의 공집합이 아닌 부분집합이 위로 유계이면(수학에서 집합이나 함수가 유한한 범위를 가지는 상태) 그 부분집합은 상한(sup B, 최소상계)을 가진다 
실수의 완비성에 관한 설명: https://www.youtube.com/watch?v=wFI7K9AHi10&t=4s

 

이제 커널에 관해 다음의 성질이 만족한다. 

 

 

 

이중 5는 의미 설명했으니 넘어가고, 4,6은 추가되었으니 한번 보자. 

 

또한 9는 커널의 합이 무한개의 특징의 합으로도 확장 가능함을 보여준다. 

양의 정부호 함수(Positive Definite Functions)

이제 양의 정부호 함수, 영어로 더 익숙한 Positive Definite Function이 무엇인지 알아보자. 

 

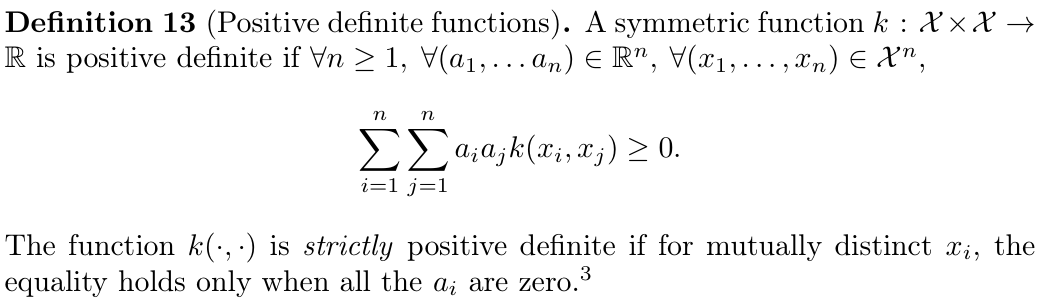
이는 쉽게 말해 어떤 선형조합을 만들어도 커널에 관한 그 값이 0 이상이어야한다는 것을 의미합니다. 

우리는 보통 해당 용어를 matrix에서 더 많이 사용하는데 이는 matrix의 일반화된(무한 차원으로의 확장)이 function form이라고 보면 된다. 

즉, PDF에을 가지고 matrix를 구성하면 해당 행렬은 postive definite matrix이다. 

 

또한 strictly positive definite(not semi)라는 것은 서로 다른 xi 에 대해 위 식이 오직 모든 ai=0일 때만 성립하는 경우를 의미한다(즉 0이 포함되냐 안되냐의 차이)

모든 내적(inner product) 은 양의 정부호 함수이며, 일반적으로 다음 성질을 가집니다.

Reproducing Kernel Hilbert Space (RKHS)

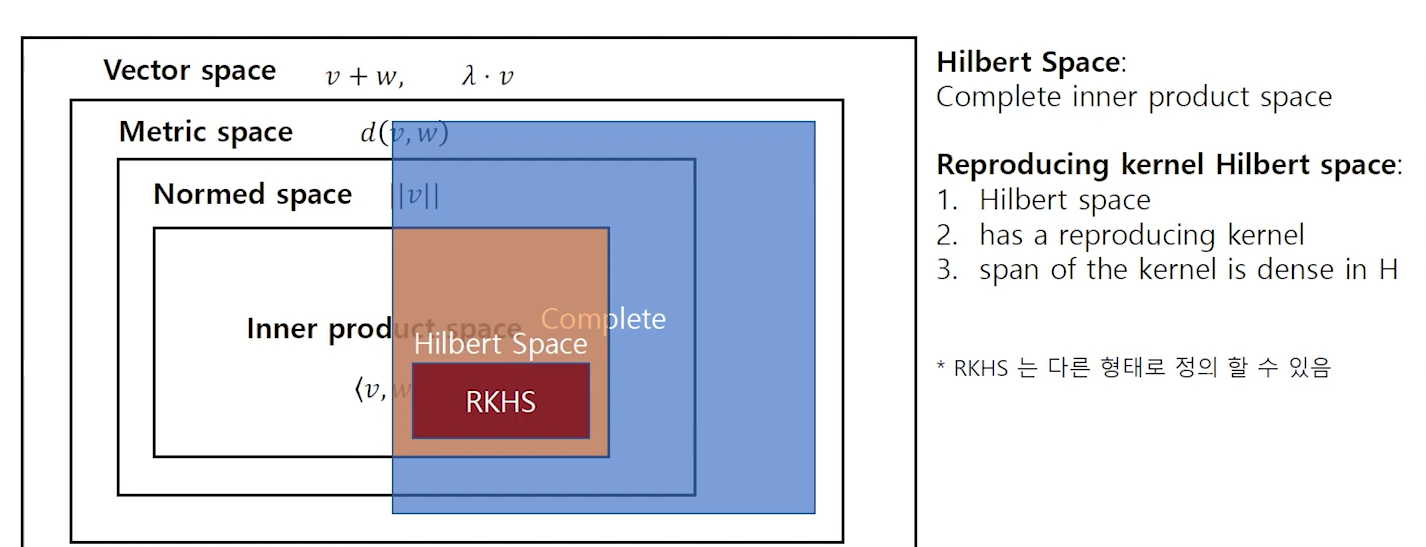
출처: 고려대학교 데이터사이언스 플러스 강의

 

앞서 특징 공간(feature space) 및 커널(kernel) 의 개념을 도입하였고, 이러한 커널이 양의 정부호(positive definite) 임을 확인했다

이제, 이러한 커널을 활용하여 함수 공간(function space) 을 정의하고, 이를 통해 재생 커널 힐베르트 공간(RKHS)을 알아보자.

 

4.1.1 Finite dimensional setting - motivation and Reproducing property 

우선 다음과 같은 유한 차원의 feature space를 가정하자. Feature map을 아래와 같이 가정하자. 

 

그럼 커널함수는 고차원에 맵핑된 값들에 관한 내적으로 정의된다. 

 

이제 우리가 다루는 함수에 관해 보자.  feature x1, x2, x1x2를 사용하려믄 함수를 f(x)라고 하자. 즉, 아래와 같다

 

이는 R2 공간에서 R1으로 매핑하는 함수이다(입력벡터 x1, x2를 받아 특정 값으로 반환). 

그러면 우리는 f를 아래와 같이 표현가능하다(입력벡터를 받아 a, b, c 계수를 할당)

 

우리는 이를 다음과 같은 표기로도 변경가능하다. 

 

즉 f에서의 x의 값은 Feature space H에서 내적으로도 표현할 수 있다. 이때 H는 R2에서 R로 매핑하는 함수들의 공간이다. 

이것이 재생속성, Reproducting Property이다. 

 

 

 

 

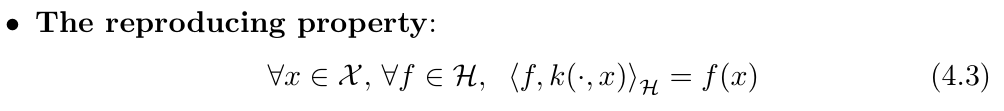
RKHS, 재생 커널 힐베르트 공간(RKHS)는 그럼 이러한 재생속성을 가지는 힐버트 공간으로 정의할 수 있다.

즉, 양의 정부호 커널을 통해 정의된 함수 공간이며 ==  RKHS와 PSD한 Kernel 은 1대1 대응관계이다(이는 Mercer's Theorem에 의해 중요한 특징이다)라고 생각할 수 있다. 

통계적인 관점에서는 아래와 같이 생각할 수 있다고 한다.