[Out of Distribution Detection(CPD)][Parameter] Neural Mean Discrepancy for Efficient Out-of-Distribution Detection (CVPR 2022)

https://arxiv.org/abs/2104.11408

Neural Mean Discrepancy for Efficient Out-of-Distribution Detection

Keypoint

NMD가 Integral probability metrics에서 사용되는 witness function으로 인스턴스화 되어 사용가능하다. 

Abstract

Out of distribution, OOD를 발견하는 것은 여러모로 중요하며, 모델, 입력 예제 및 학습데이터, 최적화 등을 증강시키는데 다양한 방법론들이 제시되어왔다. 기존 방법들과 다르게 본 논문에서는 off-the-shelf 모델이(사전학습된 모델) 이미 학습 데이터의 분포에 관하여 충분한 정보를 가지고 있으며, 이를 활용하여 신뢰할 수 있는 OOD 탐지가 가능하다는 가설을 세웠다. 

 

이를 위하여 OOD 및 In-Distribution(ID) mini batch에 대한 모델의 activation means를 측정한 결과, 학습 데이터의 activation mean과의 편차가 일관되게 있음을 확인할 수 있었다. 또한 이런 학습데이터의 activation mean은 오프라인에서 계산 가능하며, batch norm layer에서 가져올 수도 있다(as a free lunch). 이런 결과를 바탕으로 입력 예제(train dataset)과 학습 데이터의 neural mean을 비교하는 NMD, Neural Mean Discrepancy (NMD)를 제안한다. 또한 forward pass 이후 단순한 분류 모델을 적용하는 방법으로 NMD 평균을 계산하는 효율적인 classifier를 설계했고 제안한다. 

Fig2: The pipeline of NMD-based OOD detection. An input example’s NMD vector is computed by taking the difference between its channel-wise activation mean and corresponding running average in the batch normalization (BN) layer. The NMD vector is then passed to a lightweight classifier (e.g., LR or MLP). Please be advised that BN is not a requirement in computing NMD.

Activation mean:
특정 layer에서 활성화 값들의 평균을 의미, 즉 activation function의 output, Fig2에서 Input’s Neural Mean의 avg에 해

Neural mean: 
여러 계층에서 구한 Activation mean의 집합 혹은 동일 의미로 사용

Batch Normalization (BN) Layer:
배치 정규화(Batch Normalization, BN) 계층은 훈련 데이터의 평균 및 분산을 저장하여 정구화하는 layer
훈련 데이터의 Activation Mean을 미리 저장하고 있다고 봐도 무방
(https://gaussian37.github.io/dl-concept-batchnorm/ 참고하면 개념에 도움됨)

Nerual Mean Discrepancy:

Introduction

Deep Neural Networks, DNN은 많은 컴퓨터 비전 작업에서 성공을 거두었다. 그러나 대부분의 딥러닝 방법은 데이터가 독립적이며 동일한 분포(i.i.d.)를 따른다는 가정을 기반으로 한다. 즉, 훈련 데이터와 테스트 데이터가 동일한 기본 분포에서 온다고 가정한다. 하지만 현실 세계의 다양한 시나리오를 모두 포함하는 데이터셋을 구성하는 것은 거의 불가능하며, 따라서 i.i.d. 가정은 실제로 성립하지 않고 테스트 데이터에서 분포 밖(out-of-distribution, OOD) 예제가 발생할 가능성이 크다. 따라서 심층 신경망을 real world application에 적용할때 OOD 예제를 탐지하는 능력이 필수적이다.

OOD 예제를 다루기 위해 여러 접근 방식이 개발되었다. 대표적으로 표준 DNN 아키텍처를 개선하는 방법과 증강된 훈련 데이터셋을 활용한 DNN 미세 조정(fine-tuning) 기법이 있다. 그러나 이러한 방법들은 계산 및 데이터 처리 측면에서 상당한 오버헤드를 초래하는 경우가 많다.  최근 연구들은 표준 훈련 데이터셋에서 커널 밀도 추정을 수행하고, 들어오는 예제의 밀도의 음수를 이상치 점수(outlier score)로 해석하는 방식을 제안했다[22, 31, 44, 63]. 기존 연구에서는 비모수적(non-parametric) 및 모수적(parametric) 커널을 모두 활용했지만, 이러한 방법들은 성능이 제한적이며, 대규모 배치 크기에 대한 높은 의존성과 낮은 계산 효율성을 가지는 단점이 있다.

이전 연구들과 달리, 우리는 사전 학습된 모델 자체가 훈련 데이터 분포에 대한 충분한 정보를 포함하고 있다고 가정한다(we believe the off the-shelf model itself should contain sufficient information about the training data distribution). 

따라서 OOD 및 ID(분포 내) 입력 배치에 대해 모델 Activation mean(활성화 평균)을 분석하는 간단한 연구(Figure 3)를 수행하였다. 그 결과, OOD 미니배치의 activation mean 이 훈련 데이터의 activation mean과 비교하여 일관되게 크게 벗어난다는 점을 발견하였다. 이를 바탕으로, OOD 탐지가 모델의 미세 조정 없이도 단순히 활성화의 산술 평균을 계산하는 것만큼 간단하고 효율적일 수 있는지에 대한 질문을 제기하였다.

본 논문은 입력 예제와 훈련 데이터의 신경 평균(neural mean)을 비교하는 새로운 지표인 Neural Mean Discrepancy(NMD)를 제안한다. 이 NMD 지표는 모델의 활성화 값에서 효율적으로 계산할 수 있으며, 순전파(forward pass) 연산만으로도 충분하다. 또한, 훈련 데이터의 neural means는 Batch Normalization 계층에서 추가 비용 없이 얻을 수 있다[43]. 실험 결과, 제안된 NMD 지표는 OOD 탐지에서 높은 정확도와 효율성을 동시에 달성하는 것으로 나타났다(Figure 1).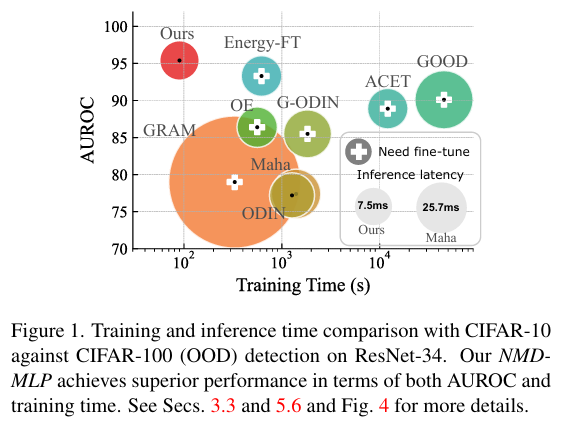

 

 

이론적 관점에서, 우리는 앞서 언급한 관찰 결과와 NMD(Neural Mean Discrepancy) 공식화를 적분 확률 거리(integral probability metrics, IPMs)와 연결시킨다. IPM은 일반적인 분포 거리(metric) 계열로, 두 개의 데이터 집합을 특정 커널을 통해 새로운 공간으로 투영한 후, 투영된 값들의 평균 차이를 분포 간 거리로 사용하는 방식이다.

기존 연구에서는 비모수적(non-parametric) 및 DNN 기반 커널이 모두 연구되었다[31, 44, 63]. 본 논문의 연구의 핵심 발견은, 별도의 커널 함수를 정의하는 대신, 사전 학습된(off-the-shelf) 심층 신경망 자체가 OOD 탐지를 위한 효율적이고 효과적인 커널 역할을 수행할 수 있다는 점이다. 이 발견은 다음과 같은 몇 가지 이점을 제공한다.

1. 접근성(Accessibility): 사전 학습된 DNN을 직접 활용할 수 있으므로, NMD 거리 지표는 데이터 및 계산 집약적인 커널 최적화, 모델 미세 조정(fine-tuning), 하이퍼파라미터 탐색을 필요로 하지 않는다.
2. 확장성(Extensibility): 각 뉴런 그룹(예: 합성곱 계층의 각 채널)은 개별적인 커널로 간주될 수 있으며, 이를 통해 수천 개의 병렬 커널을 사용할 수 있다. 이러한 커널들은 DNN의 다양한 깊이에서 추출되며 서로 보완적으로 작용하여 다중 수준의 의미적 특징을 포착할 수 있어, 분류 성능이 향상된다.
3. 단순성(Simplicity): NMD 지표의 계산은 놀랍게도 DNN 활성화 값의 평균을 계산하는 것만큼 간단하다. 훈련 데이터에 대한 순전파(forward pass)만으로 사전 계산할 수 있다. 더욱 흥미로운 점은, 모델에 배치 정규화(Batch Normalization, BN) 계층이 포함되어 있다면, 신경 평균을 BN 계층에서 직접 근사할 수 있어 추가 비용 없이 얻을 수 있다. 

우리는 NMD(Neural Mean Discrepancy)의 절댓값이 배치 크기가 4까지 감소하더라도 ID(분포 내)와 OOD(분포 밖) 배치를 안정적으로 구별할 수 있음을 발견했다. 이는 기존 통계적 방법들보다 한 차원 작은 배치 크기에서도 효과적으로 작동함을 의미한[13, 27, 30, 31, 44].

Figure 3는 CIFAR-10의 Resnet 예제

 

탐지 성능을 더욱 향상시키기 위해, 우리는 가벼운(lightweight) OOD 탐지 모델을 도입하였다. 이 모델은 로지스틱 회귀(logistic regression) 또는 다층 퍼셉트론(multilayer perceptron)으로 구현되며, neural means을 입력으로 받아 탐지 결과를 생성한다. 이 탐지 모델은 NMD 벡터 내 요소들의 민감도(sensitivity)와 상관관계(correlation)를 고려할 수 있으며, 배치 크기가 1일 때(즉, 단일 샘플 OOD 탐지)에도 최첨단(state-of-the-art) 탐지 정확도를 달성할 수 있다. 전체 방법론의 파이프라인은 Figure 2 및 Algorithm 1에 나와 있다.

 

우리는 NMD를 다양한 데이터셋, OOD 유형(far & near OOD), 사전 학습 방식( su pervised and self-supervised [34]) , 그리고 모델 아키텍처(Simple ConvNet[44], ResNet[35], VGG[80], Vision Transformer[19])에 걸쳐 광범위하게 평가하였다.

 

NMD는 이러한 환경에서 통계적 접근법 및 기존 최첨단 방법보다 일관되게 우수한 성능을 보였다. 또한, 우리는 다양한 데이터 조건에서 NMD의 견고성(robustness)과 일반화 가능성(generalizability)을 평가하였다. 여기에는 소수 샘플(few-shot) ID 및 OOD 예제, 사전 학습 없이(zero-shot) OOD 예제를 탐지하는 경우, 그리고 unseen OOD에 대한 전이 학습(transfer learning) 시나리오가 포함된다.

추가적으로, 우리는 제안한 접근법의 효율성을 측정하였으며, NMD 탐지기의 학습 비용이 기존 방법[12, 51, 58, 86]보다 수십 배 빠름을 확인했다. 또한, 전체 추론 지연 시간(inference latency)은 표준 순전파(forward pass) 연산과 유사한 수준으로 나타났다.

 

2. Prelimninary 

2.1. Out-of-distribution (OOD) detection

 확률분포 P로부터 온 훈련 집합 Dtr = {s1, ... si}에 대해 잘 훈련된 모델이 있다고 가정하자. 이후 미지의 확률분포 Q에서 온 입력 배치 예제, I가 주어졌을 때, OOD detection의 목표는 I가 P에서 왔는지를 구분하는 것이다. 이는 Q가 P에서 얼마나 벗어나는지를 측정하는 것과 유사한 맥락에서 이루어진다. 

OOD와 Change point detection의 연관성? 

2.2.Integral probability metrics

적분 확률 측도(Integral Probability Metrics, IPMs) [64]는 확률 분포 간 거리 측도의 한 종류로, 다음과 같이 정의된다.

 

여기서 ϕ(⋅)는 Witness Function을 의미한다. 

IPMs는 두 확률 분포 P와 Q의 샘플을 새로운 공간으로 사영(projection)한 후, 변환된 샘플들의 평균을 비교하는 방식이다.

일반적으로 정확한 분포의 수식을 알지 못하므로, 식 (1)은 경험적으로 다음과 같이 추정된다. 

P 와 Q 에 대한 기대값을 각각 샘플 평균으로 근사

 

 

만약 I가 OOD(Out-of-Distribution) 배치라면, 식 (2)의 값이 커질 것으로 예상되며, 그렇지 않다면 상대적으로 작은 값을 가져야 한다.

IPM은 witness function F의 적절한 클래스를 선택하는 것에 의존하는 일반적인 프레임워크이다. 하지만, IPM 기반 방법들은 몇 가지 한계를 가진다.
(1) 고차원 데이터(예: 이미지 [46])를 다루거나 의미론적 정보를 포착하는 데 어려움을 겪을 수 있다 [13, 57].
(2) 보통 가설 검정(hypothesis testing)에 의존하는데, 이는 충분히 큰 I와 Dtr의 cardinality(예: 50 이상)를 요구하고, 단일 배치당 많은 연산 반복 횟수(예: 1000 이상)를 요구한다 [27, 30, 44, 70].

https://www.youtube.com/watch?v=QKaZVqFwKqg
KMOOC에 관련 내용이 정리되어있어서 보면 좋을 것 같다

간단히 정리하면 특정 함수 집합이 두 분포를 얼마나 잘 구별할 수 있는지를 평가하는 측도로, 특히 divergence와 비교하면 분포의 비율로 그 차이를 측정하는지와 기대값의 차로 그 사이를 측정하는지의 차이이다. 
아래의 Distrance들이 대표적이다. 
와서스타인 거리(Wasserstein Distance): 함수 집합 F를 1-립시츠 연속 함수로 정의하여, 두 분포 간의 최소 비용 이동을 측정
최대 평균 차이(Maximum Mean Discrepancy, MMD): 재생 커널 힐베르트 공간(RKHS)의 단위 볼에 속하는 함수 집합을 사용하여, 두 분포의 평균 임베딩 간의 차이를 측정

3.Our approach

IPMS에 사용되는 witness funtion을 새로 정의하는 대신에 기존 사전학습된 모델을 활용화여 이를 정의할 수 있으며 이는  Neural Mean Discrepancy(NMD)이다라는 것이 본 논문의 핵심 아이디어이다. 

3.1.Neural Mean Discrepancy

3.1.1 Single-layer NMD 

IPMS와 연결을 위해 식 2를 보자. Eq 2의 식의 상한을 취한다는 것은 결국 신경망이 Q와 P에 대한 기대값 차이를 최대화하는 방향으로 최적화되는 것과 같다. 다만 이러한 과정은 높은 계산 비용을 초래하기에, 우리는 OOD 탐지의 맥락에서 해당 상한 요구 조건을 오나화하는 방안을 제안하며, 이를 위한

직관적인 가정: 만일 어떤 함수가 투영된(i.e. feature) space에서 내부분포와(in distribution) 외부분포(out distribution)의 통계량(ie: 평균)을 구별할 수 있다면, 그 함수는 적절한 witness funtion으로 간주될 수 있다. 

라는 가정을 도입힌다. 우리는 in-distribution으로 사전학습된 모델이 f(.)가 이를 만족할 수 있음을 발견했다. 

 

사전학습된 모델의 l번째 layer에서 특정 채널 c를 함수 fc로 정의하자. 이는 아래와 같다. 

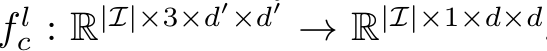
여기서 d는 입력 이미지 및 activation map의 크기를 의미한다. 

 

우리는 모델에 구애받지 않는(model-agnostic metric) metirc NMD를 이용하여 witness fucntion으로 정의한다. 

이는 아래와 같다. 

 

IPM에서 수식의 두 항의 Expectation이 취해져있기에, f를 이용하여 이와 비슷한 형태를 취해보자. 

즉, activation map의 spatial position (m,n)을 합산하여 평균을 취하여 따라서 채널 내 spatial positon의 평균(즉, 커널의 출력)을 취하는 것은 신경망을 사용한 IPM의 충실한 구현형태이다. 

 

수식에서 제일 바깥쪽의 시그마는 example(data set, batch)에 대해 수행되며

 

남은 두 시그마는 해당 채널 내의 모든 (m,n)에 대하여 수행된다. 

 

결국 식(5)는 IPM을 f를 이용해 구현한 것이고, 이때 첫번째 항은 L 즉 test data의 미니배치에 관한 activation fuction의 평균을 두번째 항은 훈련 데이터 셋에 관한 것임으로 두 분포 Q와 P에 관한 추정치이다. 

 

각각의 spatial positon은 대응되는 input image의 patch(recpetive field)에 해당함으로 결과적으로 spatial position의 평균을 취하는 것은 입력 패리를 f를 이용하여 투영한 후 평균을 내는 것과 같다. 이는  암묵적으로 입력 배치를 증강하며, 이전 IPM 기반 방법들과 비교할 때 극도로 작은 배치 크기 I (심지어 단일 입력 이미지 I=1 에 대해서도)에서도 안정적으로 동작할 수 있도록 한다.

 

 

3.1.2 Multi-layer NMD for multi-scale OOD detection

성능을 더욱 향상시키기 위해 단일 layer에서 뿐만 아니라 muti layer에서의 NDM를 측정하고 결합하는 방법에 관해 본 장에서 고려한다. 이를 통해 주어진 입력 배치 L 에 관하여 NMD 벡터를 다음과 같이 정의한다. 

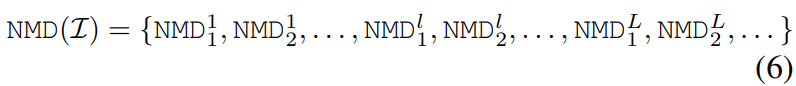
channel 1~C까지 존재, 각 채널별 1~l은 모델의 layer 수

이는 C-dim vector로 구성되며(즉 각 layer 별로 있는 채널들의 총합 C), 이때 C는 모델의 전체 channel 수(channel 종류가 아님! 개인적으로 순간 햇갈림)이다. 다층 NMD는 다음의 장점을 가진다. 

 

• 다양한 witness function 함수  사용: 각 신경망 평균 차이 NMD(l,c)는 고유한 witness funtion인  f(l,c)​ 와 1대1대응된다. 본 방법은 여러 f(l,c) 조합을 활용하므로, 단일 IPM(Integral Probability Metric) 기반 접근법보다 더 풍부한 표현력을 제공하며 이는 실험을 통해 검증된다(이후 experiment sector확인).
• Different Patch size
  서로 다른 층에서의 NMD(l,c) 는 서로 다른 패치 크기를 가질 수 있다. 이는 층의 깊이에 따라 receptive field의 크기가 선형적으로 증가하기 때문이다. 따라서 모든 층에서의 NMD를 결합하면, 저수준 및 고수준 의미 정보를 모두 포착할 수 있는 다중 스케일 OOD 탐지가 가능하다(Section 5.7 참조).
• 추가적인 계산 비용 없음
  여러 채널을 활용하더라도, NMD는 모델의 단일 순전파(forward pass)를 통해 얻을 수 있으므로 추가적인 계산 오버헤드를 발생시키지 않는다.

 

3.1.3 Free lunch from Batch Normalization

NMD가 activation statistics를 계산하는 방법은 Batch normalization와 동일하다. 식 (4)에서 u[f(Dtr)]를 모든 training data를 순회하며 계산하는 대신 BN의 running average를 사용가능하다. 

 

Batch Normalization은 modern DNN에서 필수적인 구성요소로(distribution shift 강건, 일반화 등 장점) 이는 channel별 통계량을 이용하여 정규화된 input을 계산한다. 구체적으로 activation mean을 빼고 표준편차로 나눈다. 즉 훈련과정에서 이 평균과 표준편차는 현재 미니배치의 emperical mean과 std를 이용해 계산되고, test에서는 batch별이 아닌 train set에서 추정된 기대 통계량을 사용한다. 

Ioffe et al. [43]은 기대 통계량을 효율적으로 추정하기 위해 running avergae 를 사용할 수 있음을 제안하며, 이는 다음과 같이 정의된다.

[43] Sergey Ioffe and Christian Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In ICML, pages 448–456. PMLR, 2015

 

조금 더 쉽게 설명하면 다음과 같음. 즉 모든 누적값을 이용해서 평균을 구하는 방법 

여기서, 일반적인 λ값은 0.99이며, 이는 대부분의 딥러닝 라이브러리에서 표준적으로 구현된 방식이다 [2, 68]. 

 

그럼 우리의 논문에서 제안한 방법에서도, train data의 평균을 계산하는 대신에  BN에 저장된 expectation, 즉 기대 평균을 사용할 수 있을 것이다. 

 

실험을 통해 이 근사가 OOD(Out-of-Distribution) 탐지에서 효율적으로 작동함을 검증하였다. 또한, BN을 포함하지 않는 모델(VGG [80] 및 Transformer [19] 등)에 대해서도 식 (4)의 유효성을 추가로 검증하였다.

 

3.2 A proof of concept 

논문의 아이디어를 검증하기 위하여(NMD가 IPM의 함수로 사용가능하다), in-distribution으로 CIFAR-10 데이터를 , out-of distribution으로 SVHN 데이터를 이용한다. 

 

모델로는 ResNet-34 모델을 CIFAR-10에 관하여 훈려시키고 이를 off-the-shelf 모델로 사용한다. 

주어진 미니배치 L에 관하여 NMD 벡터는 식 (5), (6- multi layer), (8-batch norm 이용)를 이용하여 계산된다. 

 

본 논문에서는 OOD 탐지를 위해, NMD 벡터 내의 요소들의 크기의 평균을 cofindence score로 사용하는 Ours-Avg를 제안함. 

CIFAR-10 (녹색 점) 및 SVHN (빨간색 점) 테스트 세트에서 각각 무작위로 100개의 미니배치를 샘플링하고, 각 배치의 점수를 Fig 3에 시각화하였다. Fig 3의 결과는: OOD 데이터는 평균적으로 내부 분포 데이터보다 더 큰 NMD 값을 가진다 는 직관을 확인시켜준다. 

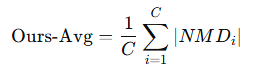
예를 들어, 
ID 데이터 (CIFAR-10)에서 나온 NMD 벡터 예시: [0.05,0.03,0.02,0.04]이고
OOD 데이터 (SVHN)에서 나온 NMD 벡터 예시: [0.35,0.42,0.38,0.40]이면
Ours-Avgs는 이 둘 각각의 절대값의 평균인 0.035, 0.3875로 주어지며 이 둘이 특정 threshold보다 큰지 작은지로 판단 가능. 

 

추가적으로 추가 학습, 모델 미세 조정(fine-tuning), 또는 하이퍼파라미터 튜닝 없이, Ours-Avg는 배치 크기 |I| = 4 일 때 99.9%의 AUROC라는 인상적인 성능을 달성하였고, 이는 다른 IPM 기반 방법들에 비해 훨씬 더 작은 배치 크기를 요구이다 [27, 30, 70].

3.3 A sensitivity-aware NMD detector

OOD 탐지의 판별력을 더욱 향상시키기 위해, 우리는 단순히 NMD 벡터의 평균을 취하는 대신, NMD 벡터 자체를 입력으로 사용하는 파라메트릭 탐지기(parametric detector)를 학습하는 방법을 제안한다. 이를 통해 배치 크기가 1(즉, L의 cardinality가 1)로 감소하더라도 탐지 성능을 향상시키고자 한다. 
기존 연구 [9, 18, 32]에서는 심층 신경망의 채널들이 서로 상관관계를 가지며, 각 채널의 중요도가 다름을 관찰하였다. 이러한 점을 활용하기 위해, NMD(x)를 입력으로 받아 현재 샘플이 OOD인지 여부를 예측하는 탐지기 g(⋅)를 학습할 것을 제안한다. 

이는 단순히 0,1을 분류하는 이진 분류 문제이며 본 논문에서는 가장 단순화된 로지스틱 회귀 기반 탐지기(LR)와 다층 퍼셉트론 기반 탐지기 (MLP)를 통해 이를 구현한다. 

 

실험 섹션에서 우리는 이 탐지기가 적은 샷(few-shot) 예제만으로도 학습할 수 있으며, 보지 못한(unseen) OOD 유형에 대해 높은 일반화 성능을 가짐을 보인다. 심지어 OOD 예제에 접근할 수 없는 경우에도, 내부 분포 예제의 픽셀을 무작위로 섞는 방식 [73]을 통해 우수한 성능을 유지할 수 있음을 보인다. 

 

알고리즘 1은 OOD detction 알고리즘의 대략적인 개요를 설명하고 있음. 그 단계를 보면

- Input (입력)
(1)입력 데이터 𝑥
(2) off-the-shelf pre-trained classifier𝑓(𝑥): CIFAR-10에서 학습된 ResNet-34와 같은 모델
(3) OOD 탐지기 𝑔(⋅) (Logistic Regression 또는 MLP 기반 OOD 탐지기)

 

-Stage 1: NMD 벡터 생성 (Feature Mean Discrepancy Vector 생성)
1. 입력 데이터 𝑥
x 를 사전 학습된 모델 𝑓(𝑥)에 전달 (Forward Pass 수행)
2. 각 채널에서 𝑁𝑀𝐷(𝑥) (Eq. (5), (6), (8) 이용) 계산
즉, 입력 데이터의 활성화 평균과 훈련 데이터(Batch norm layer이용)의 러닝 평균 간 차이를 계산.
3. 모든 채널의 NMD 값을 하나의 벡터로 연결(Concatenate)하여 NMD 벡터 𝑁𝑀𝐷(𝑥)

 

-Stage 2: OOD 탐지 수행: NMD 벡터를 사용하여 OOD 탐지를 수행하는 과정
1. 훈련(Training) 단계
OOD 탐지기 𝑔(⋅) 를 학습, 학습 데이터로 ID 데이터셋 𝑥ID 와 OOD 데이터셋 𝑥OOD의 NMD 벡터와 정답(0 또는 1) 쌍을 사용

ID 데이터 (CIFAR-10) → 레이블 0
OOD 데이터 (SVHN) → 레이블 1
2. 테스트(Testing) 단계
새로운 입력 데이터 𝑥 NMD 벡터를 생성.
학습된 OOD 탐지기  g(NMD(x)) 를 사용하여 OOD 여부 판별.

 

4. Experimental setup

 4.1 Off-the-shelf models

NMD는 model-agnostic한 방법이며 아래의 다양한 모델 아키텍쳐에서 이를 평가한다. 실험에 사용된 모델은 4-layer ConvNet , ResNet-34 , self-supervised ResNet-34, WideResNet, DenseNet-100, VGG, 그리고 Vision Transformer 이다. 모든 모델은 원래의 학습절차(original training receipts)를 통해 충분히 훈련된 후, 실험 동안은 forzen(파라미터 고정, 추가 미세조정 없음)된 상태로 사용된다. 

 4.2 Benchmark datasets

데이터셋	채널	Class	Train	Test	주요 특징
CIFAR-10	RGB	10	50,000	10,000	10개의 일반적인 클래스(예: 비행기, 자동차 등)로 구성된 소형 컬러 이미지. 딥러닝 모델 성능 비교에 자주 사용됨.
CIFAR-100	RGB	100	50,000	10,000	CIFAR-10의 확장판으로, 더 세분화된 100개의 클래스 제공. 복잡한 분류 작업에 적합.
SVHN	RGB	10	73,257	26,032	거리 번호판에서 추출된 숫자 이미지. 숫자 인식 모델 학습에 사용되며, 중간 숫자를 예측하는 것이 목표.
MNIST	Gray	10	60,000	10,000	손으로 쓴 숫자(0~9) 이미지. 딥러닝 입문 및 기본적인 분류 알고리즘 테스트에 적합.
ImageNet	RGB	1,000	1,281,167	약 50,000	대규모 데이터셋으로 다양한 객체 분류 및 전이 학습에 사용됨. ILSVRC 챌린지에서 널리 활용.
COCO	RGB	약 80	330,000	-	객체 검출, 이미지 캡셔닝 등 다양한 태스크를 위해 설계된 데이터셋. 다중 객체와 정밀한 주석 제공.
STL-10	RGB	10	5,000	8,000	CIFAR-10 기반으로 더 큰 해상도를 가지며 소량의 학습 데이터 제공. 전이 학습 실험에 적합.
Fashion-MNIST	Gray	10	60,000	10,000	의류 이미지를 포함하며 MNIST와 유사한 구조. 의류 분류 모델 개발 및 테스트에 사용.
LSUN	RGB	10	3,000,000	-	대규모 장면 인식, 침실 등 10개 카테고리, 비지도 학습에 사용
iSUN	RGB	-	-	-	장면 인식 및 이해를 위한 데이터셋, LSUN의 하위집합
Textur	RGB	-	-	-	물질 표면 특성, 택스텨 패턴 인식 및 분석에 사용

 

벤치바크 데이터셋으로는 이미지에서 사용되는 CIFAR-10, CIFAR-100, SVHN, cropped ImageNet, cropped LSUN, iSUN, 그리고 Texture 데이터셋을 사용하고 이는 기존 OOD 연구 [51, 55, 58, 73, 78]를 따름. 

 

내부 분포(in-distribution, ID)와 외부 분포(out-of-distribution, OOD) 데이터셋의 조합에 따라 문제의 난이도가 달라지기에(일반적으로 더 차이가 날수록 인식이 쉽기에 near-ODD의 난이도가 더 높음) [73, 78, 92] . OOD 탐지 문제는 일반적으로 근접 OOD(near-OOD)**와 원거리 OOD(far-OOD)로 구분된다. 

 

• 근접 OOD (near-OOD): 두 데이터 분포가 서로 가까운 경우. 예를 들어, CIFAR-10을 내부 분포로, CIFAR-100을 OOD로 설정하는 경우. 두 데이터셋 모두 TinyImageNet [69]에서 유래되었으며, 라벨이 일상적인 사물(daily objects)로 구성되어 있어 의미적으로 유사함.
• 원거리 OOD (far-OOD): 내부 분포와 OOD 데이터의 차이가 큰 경우입니다. 예를 들어, CIFAR-10을 내부 분포로, SVHN을 OOD로 설정하는 경우입니다. SVHN은 집 번호 이미지로만 구성된 반면, CIFAR-10은 다양한 자연 이미지로 구성되어 있어 차이가 큽니다.

논문에서는 두 ODD에서의 실험을 모두 실행함. 

 4.3 Protocols

OOD 탐지 시나리오를 시뮬레이션하기 위해, 우리는 네 가지 데이터 접근 환경을 고려, 실험을 진행한다. 

1. Full access (전체 접근): 기존 OOD 탐지 방법들은 내부 분포(ID) 및 외부 분포(OOD) 데이터에 모두 접근할 수 있다고 가정하며, 이를 이용해 OOD 탐지기를 학습하고 하이퍼파라미터를 조정한다.
2. Few-shot (소량 샘플): 개인정보 보호 문제로 인해, 데이터 제공자가 ID 및 OOD 데이터의 일부 샘플만 공개할 수 있습니다. 실험에서는 극단적인 시나리오로, 단 25개의 ID 예제와 25개의 OOD 예제만을 사용하여 탐지기를 학습하는 방법을 제안합니다.
3. Zero-shot (제로샷): 최근 연구들 [39, 58, 78, 90]에서는 OOD 데이터를 전혀 사용하지 않고 ID 데이터만으로 OOD 탐지기를 학습하는 방법을 탐구하고 있음.
4. Transfer (전이 학습): 서로 다른 OOD 데이터셋 간의 전이 가능성을 평가하기 위해, 하나의 OOD 데이터셋에서 탐지기를 학습한 후, 보지 않은 새로운 OOD 데이터셋에서 성능을 평가하는 방식을 제안함.

4.4 Evalutation metrics

문헌 [51, 55, 58, 73, 78]에 따라, 우리는 세 가지 평가 지표를 사용한다:

(1) true negative rate at 95% true positive rate (TNR95),

(2) area under the receiver operating characteristic curve (AUROC)

(3) detection accuracy (ACC) which measures the maximum detection accuracy over 모든 가능한 임계값 

 

4.5 Baseline methods

Baseline methods는 크게 통계적 방법과 Other baslines으로 나누어진다. 

1. Statistical methods:

Sheng et al.[44]d에서 밝힌 바와 같이, 테스트 샘플 x에  관하여, 통계적 방법들은 negative sum of kernel evaluation of inliner example(내재 샘플, Sx)를 이용하여 OOD 점수를 계산한다. 즉,

 

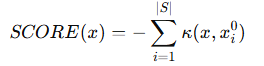
이며, 커널의 종류에 따라 다양한 방법이 결정되며 Deep kernel (DK [27, 57]), convolution neural tangent kernel (CNTK [6]), and shift-invariant convolutional neural tangent kernel (SCNTK [44])이 대표적이다. 

 

2. Other baselines:

ODIN [55], 마할라노비스 거리(Mahalanobis distance) [51], 분류기 미세 조정을 포함한 OE(OE with classifier fine-tuning) [38], 그리고 분류기 미세 조정을 포함한 에너지 방법(Energy with classifier fine-tuning) [58]과 같은 최신 기술들을 basline으로 삼는다. 이러한 방법들은 하이퍼파라미터 튜닝과 fine-tuning, multi-round forward inference(순전파 여러번하기)가 포함되나 NMD는 필요치 아니한다. 

5. Results

모든 결과는 단일 샘플 탐지에 대해 얻어졌으며, 즉 배치 크기는 1이다. 

5.1 Comparison with statistical baselines

통계적 검정을 기반으로 한 가장 관련성이 높은 접근 방식인 DK [27, 57], CNTK [6], SCNTK [44]와 우리의 방법을 비교한다. 이러한 방법들은 각 테스트 샘플마다 내재 분포 데이터 𝑆의 일부를 탐색해야 하므로 계산 비용이 클 수 있다. 반면, NMD는 𝑆에 의존하지 않기 때문에 더 높은 효율성을 가진다.

 

Sheng et al. [44]의 설정을 따르며, 비교된 모든 방법은 4-layer convolutional neural network 을 feature extracoer로 사용한다. 표 1에서 볼 수 있듯이, 우리의 방법(로지스틱 회귀 탐지를 사용하는 'Ours-LR')은 OOD 탐지 성능에서 유의미한 향상(99.8% 이상의 AUROC)을 달성한다. 이 결과는 동일한 사전 학습된 모델에서 다양한 스케일과 의미적 수준의 multiple witness functions를 사용하는 것이 가치가 있음을 실증적으로 입증한다(empirically justifies).

 

5.2. Comparison with other baselines

 

CIFAR-10을 학습한 ResNet을 사용하여 다양한 OOD(Out of distributon) 데이터 셋에 대한 결과를 확인한다. 

이 실험에서는 In Distribution 데이터셋과 OOD 데이터셋 모두 학습이 가능하다고 자정한다. 

 

실험을 위해 NMD에서 ResNet-34은 frozen(고정)하며, 다른 방법들의 경우 테스트 검정력을 증가시키기 위하여 fin-tuning이 있을 수도 있다. 또한 NMD는 하이퍼 파라미터가 필요하지 않지만, 다른 방법들의 경우 필요로 한다.( eg temperatures in [55], perturbation in [51], and margin in [58]). 

Fig 4의 Table 버전

Fig4에서 볼 수 있듯이, NMD를 이용한 방법이 모두 일관되게 우수한 성능을 보이며,  near-OOD 데이터셋인 CIFAR-100에서 다른 방법들보다 뛰어난 성능을 발휘한다(즉, 미세한 변화도 잘 탐지함).

5.3. Learning with only in-distribution examples

 

본 장에서는 학습 시 특정 OOD 데이터셋에 의존하지 않는 방법들과 우리의 방법을 비교한다. 이러한 방법 중 G-ODIN [39]과 1D [90]는 내재 분포 데이터셋에서 모델을 미세 조정해야 한다.

실제 OOD 예제가 접근 불가능한 상황에서, 우리는 내재 분포 샘플의 픽셀을 무작위로 재배열하여 인공적인 OOD 예제를 생성하고, 이를 사용하여 탐지기를 학습시킨다(관련하여 appendix 참고) 이후, 인공적으로 생성된 OOD 예제에서 학습된 탐지기를 실제 OOD 데이터셋에서 평가한다.

그림 5에서 볼 수 있듯이, 우리의 방법은 실제 OOD 데이터를 사용하지 않고도 최신 기법보다 우수한 성능을 보인다. 또한, 비록 인공적인 OOD 예제가 현실적이지 않더라도, OOD 탐지기의 결정 경계를 효과적으로 형성하는 데 도움이 된다는 것을 보인다. 

 

5.4. Few-shot OOD training

 

본장에서는 학습에 사용할 수 있는 내재 분포(ID) 및 OOD(Out-of-Distribution) 샘플의 수가 매우 제한적인 시나리오에서 방법들을 평가한다. 

Fig 6은 학습 시 ID 샘플 25개와 OOD 샘플 25개만 사용할 경우 다양한 방법의 성능을 비교한다. 기준 방법인 ‘Gram’은 OOD 샘플에 의존하지 않기 때문에 예외적으로 50개의 ID 샘플을 사용한다. 또한, ‘Energy’ 방법의 경우 50개의 샘플만으로는 미세 조정이 어렵기 때문에, 미세 조정을 수행하지 않은 성능을 참고용으로 제공한다.

이러한 few-shot 설정에서 우리의 방법은 모든 다른 방법보다 뛰어난 성능을 보인다. 기존 연구들은 일반적으로 충분한 데이터를 필요로 하며, 하이퍼파라미터 또는 모델을 조정해야 한다. 반면, NMD는 하이퍼파라미터가 필요하지 않아 적은 샘플에서도 효과적으로 학습할 수 있다. 그러나, MLP 탐지기에서 약간의 과적합이 관찰되었으며, 이는 few-shot 환경에서는 로지스틱 회귀(LR)와 같은 낮은 용량의 모델을 고려하는 것이 바람직함을 시사한다.

 

5.5. Generalizability across models and datasets(Transfer learning)

 

위에서 밝힌것과 같이, Detecor, 즉 ODD 감지기의 데이터셋간의 transfer가 가능한지 확인해본다.

이를 위하여 각 모델에 CIFAR-100을 OOD(Out-of-Distribution) 데이터셋으로 사용하여 감지기를 학습한 후, LSUN-C, SVHN, Texture, ImageNet-C와 같은 보지 않은 OOD 데이터셋에서 학습된 감지기를 평가한다. 

 

Section 3.1에서 설명한 봐와 같이, BN(Batch Normalization)의 running  avergae을 사용하여 u[f(Dtr)]을 근사하거나(Eq. 8). 모델에 BN layer가 없을 경우 Eq.4와 같이 이를 수동으로 계싼할 수 있다. 따라서 다양하 모델에 걸쳐서 BN layer가 없는 경우에도 일반화 할 수 있는지 확인해본다. 

 

1. VGG models.: VGG-19는 16개의 convolution  및 ReLU 레이어와 3개의 fully-connected(FC) layer로 구성되어있다. 즉, BN layer가 없기 때문에 Conv layer의 채널만을 사용하여 NMD를 계산한다. 즉, 내재된 분포의 학습데이터셋(ex: CIFAR-10)을 기준으로 한 에포크동안 순회하여 평균을 계산한다. 

 

2. Self-supervised models.:  자기 지도 학습 기법으로 MoCo [34]를 사용한다, MoCo를 활용하여 ResNet-34 모델을 CIFAR-10에서 사전 학습한 후, 모델을 고정(freeze)하고 이를 사용하여 NMD를 계산한다.

 

3. Vision Transformers: 

CNN과 달리 비전 트랜스포머(ViT)는 muti-head self-attention과 position-wise fc layer를 포함하는 스택으로 구성된다. ViT는 이미지를 p개의 겹치지 않는 패치로 분할한 후, 이 패치들의 임베딩 시퀀스를 트랜스포머의 입력으로 사용한다. ViT는 각 입력 샘플의 활성화 값 Zₗ ∈ R^(p×d)을 정규화하기 위해 레이어 정규화(LN) [8]를 사용하기에 

CNN을 모방하여, 입력 샘플 x에 대해 ViT의 특징 평균을 아래와 같이 사용한다. 

 

 

표 2에서 알 수 있듯이, NMD는 다양한 모델과 데이터셋에서 높은 일반화 성능을 보이며, 흥미롭게도, selfsupervised ResNet-34  모델이 4개의 보지 않은 OOD 데이터셋에서 평균적으로 가장 높은 탐지 성능을 보이며, 이는 학습된 표현의 높은 전이 가능성을 시사한다[16, 23, 34]

5.6. Training and inference efficiency(비용)

이 섹션에서는 제안된 Ours-MLP와 Fig. 1에 제시된 기준 모델들의 학습 및 추론 비용을 비교한다.
본 논문에서는 NVIDIA GPU 1080 Ti 및 Intel(R) Xeon(R) CPU E5-2650 v4 @ 2.20GHz가 장착된 머신에서 학습 및 추론 시간을 측정하였다.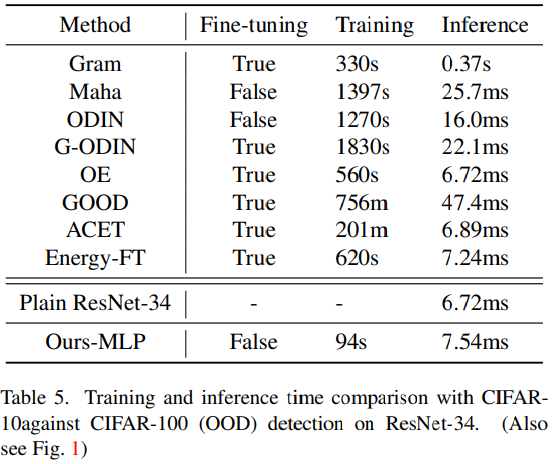

 

-Training cost.
사용된 탐지기(즉, LR 및 MLP)가 가벼운 모델이므로(lightweight)  학습 과정은 빠르게 완료될 수 있다(CIFAR-10 (ID) 및 CIFAR-100 (OOD) 학습 데이터셋을 사용한 경우 60 epoch이내, Fig. 1 참조).
또한 기존 방법과 달리, NMD는 성능에 민감한 하이퍼파라미터를 갖고 있지 않아 하이퍼파라미터를 탐색하기 위해 여러 번 학습을 반복할 필요가 없다는 장점이 있음

 

- Inference cost
Algorithm 1에서 설명한 바와 같이, 사전 학습된 모델을 사용하여 single forward pass 를 실행하는 것만으로 NMD 벡터를 생성할 수 있다.
생성된 NMD 벡터는 가벼운 탐지기(예: Sec. 3.3에서 설명한 로지스틱 회귀 또는 3 layer MLP)에 의해 처리된다.

 

반면, 다른 접근 방식은 standard forward pass (Baseline [37] and ACET [36]) 외에도 다음을 추가적으로 요구한다.
(1) 추가 forward and backward passes [39, 51, 55] 실행
(2) 복잡한 속성(예: (co-occurrences)) 계산 [78, 90]

 

그럼으로 NMD가 Trainin과 Inference 모두에서 더 저렴한 비용을 가짐을 확인가능하다. 

5.7. Ablation study

5.7.1 Layer importance for OOD detection.

 

Fig. 7에서 ResNet-34의 서로 다른 레이어에서 생성된 NMD의 중요도를 시각화하였다.
본 논문에서의 방법론은 shallow layers의 low-level 시각적 속성(visual attribute)와 deep layer에서의 high level 의미론적 정보( high-level semantic information)를 모두 활용하며 task에 따라 동적으로 중요도를 조정하는 것을 확인할 수 있다.

왼쪽 (CIFAR-10 ❘ SVHN, far-OOD): 초기(첫 번째) 레이어가 가장 중요하며, 이후 레이어에서는 중요도가 감소하는 경향. 즉, 초기 레이어의 특징이 far-OOD 탐지에 가장 유용함을 의미함. 오른쪽 (CIFAR-10 ❘ CIFAR-100, near-OOD): 마지막 레이어의 중요도가 가장 큼. 즉, 최종 레이어에서 near-OOD 데이터(CIFAR-100)와의 차이가 뚜렷하게 나타남. CIFAR-10과 CIFAR-100은 둘 다 자연 이미지 데이터셋이므로, 초기 레이어보다는 고차원 특징을 반영하는 마지막 레이어가 더 중요함.

Fig. 7의 상단의 두 그래프에서는 OOD 탐지기로 로지스틱 회귀(LR)를 사용하였다. LR 에 입력하기 전, NMD 벡터를 표준화하여 모든 차원의 크기를 유사하게 맞추었다. 
LR에서 학습된 각 계수의 절대값은 해당하는(대응하는) 채널의 중요도로 간주할 수 있으며, 우리는 레이어의 중요도를 해당 레이어 내 모든 채널의 중요도를 평균하여 계산하였다(즉 계수의 절대값의 평균)

또한 본 논문에서는 두 가지 OOD 탐지 작업을 수행하였다.
(1) far-OOD task: CIFAR-10과 SVHN 비교 실험에서는,
저수준 특징을 추출하는 얕은 레이어의(시각적인 특성) NMD 값만으로도 CIFAR-10과 SVHN을 구별할 수 있었다 [7, 88].
(2) near-OOD task : CIFAR-10과 CIFAR-100 비교 실험에서는,
의미적 차이를 포착하기 위해 더 깊은 레이어의 NMD 값이 필요하였다.

 

왼쪽 (CIFAR-10 ❘ SVHN, far-OOD) 초기 5개 레이어만 사용해도 AUROC = 99.9%반면, 첫 번째 레이어만 사용할 경우 AUROC = 84.0%즉, 초기 몇 개의 레이어만으로도 far-OOD 탐지가 매우 효과적임을 의미함. 오른쪽 (CIFAR-10 ❘ CIFAR-100, near-OOD) 사용하는 레이어 수가 많아질수록 AUROC가 점진적으로 증가near-OOD 탐지에서는 단순한 저차원 특징보다 전체적인 계층을 활용하는 것이 효과적임.

Fig. 7의 하단 두 그래프는 처음 k개의 레이어에서 생성된 NMD만을 사용했을 때의 탐지 성능을 시각화한 것이다.
SVHN과의 비교에서는 첫 5개 레이어만으로도 최고 AUROC 성능을 달성할 수 있었던 반면,
CIFAR-100과의 비교에서는 더 많은 레이어를 사용할수록 성능이 지속적으로 향상되었다.

 

이러한 관찰 결과는 앞서 LR 모델에서의  내용과 일치하며, 입력 샘플에 따라 적절한 레이어를 동적으로 선택하는 '조기 종료(early exits)' 방식을 적용하면 성능과 효율성을 더욱 향상할 가능성이 있음을 시사한다 [56].

5.7.2 Does Neural Variance Discrepancy help? 
평균(mean)과 같은 first order statistics 뿐만 아니라, 뉴럴 네트워크 활성값의 second order statistic을 활용한 Neural Variance Discrepancy(NVD) 개념도 정의할 수 있다.
실험 결과, NVD를 사용한 경우(OOD 탐지 성능: AUROC=95.3, CIFAR-10 대 CIFAR-100, ResNet-34)는
NMD 단독 사용(AUROC=95.4)과 유사한 OOD 탐지 성능을 달성하였다. 또한, NMD와 NVD를 결합하면 성능이 소폭 향상되었으며(AUROC=95.6), 자세한 내용은 Appendix E를 참고.

6. Related work

6.1.1 OOD detection with model modification and fine-tuning

여러 OOD 접근법에서는 표준 DNN 아키텍처를 다음과 같이 확장한다.

• 모델 앙상블을 활용한 방법 [14, 26, 48, 83]
• 추가적인 가지(branch) 학습을 통한 방법 [17, 33]
• 배경 모델 학습을 이용한 방법 [73]

또한, 다양한 새로운 학습 목표가 제안되었다. 예를 들면,

• OOD 균일 라벨(uniform label)로 학습하는 방법 [50]
• 추가적인 OOD 클래스를 도입하는 방법 [15, 61]
• 생성 모델을 활용하여 OOD 샘플을 생성하는 방법 [62]
• 에너지 스코어 정규화 기법 [58]
• 소프트-비닝(soft-binning) 오류 보정 기법 [45] 등이 있다.

6.2.2 OOD detection without fine-tuning.

최대 소프트맥스 확률(Maximum Softmax Probability, MSP) [37] 및 그 변형 모델들이 OOD 탐지에 사용된다.

• ODIN [55], GODIN [39], POOD [24], Energy [58] 등 MSP 기반 접근법이 대표적이다.

최종 출력뿐만 아니라 중간 활성값(intermediate activation) 을 활용하는 방법도 연구되었다.

• Gram 특징 기반 방법 [78]
• 마할라노비스 거리(Mahalanobis distance) 기반 방법 [51, 72]

6.2.3 Statistical OOD detection

이전 연구에서는 프레셰 거리(Frechet distance) [20] 및 최대 평균 차이(Maximum Mean Discrepancy, MMD) [29]를 활용하여 적대적 샘플 탐지(adversarial detection) [13, 27, 30, 74] 및 분포 변화 탐지(distribution shift detection) [31, 70]에 대한 초기 실험 결과를 제시하였다.

Erdil et al. [22]는 적대적 섭동(adversarial perturbation)과 커널 밀도 추정(Kernel Density Estimation, KDE)을 활용하여
in-dristribution 샘플의 일부와 입력 데이터를 비교하는 방식으로 OOD 탐지를 수행하였다.
또한, 생성 모델을 활용한 OOD 탐지에서는 상태 밀도 추정(density of states estimator) 기법이 사용되었다 [63].

Jia et al. [44]는 적응형 심층 신경 커널(adaptive deep neural kernel) [6, 27, 57]의 변형인 합성 커널(compositional kernel)을 제안하여 보다 효율적인 OOD 탐지를 수행하였다. 그러나 이 연구에서는 주로 얕은 모델(shallow models) 만 고려되었다.

본 연구에서는 사전 학습된 모델의 뉴럴 평균(neural means) 을 창의적으로 활용함으로써, 통계적 OOD 탐지의 알고리즘적 복잡도와 계산 비용을 크게 감소 시킬 수 있었다.

6.2.4 Updating Batch Normalization statistics for improved accuracy

이전 연구에서는 배치 정규화(Batch Normalization, BN) 레이어의 통계량(statistics) 및 affine parameters 를 업데이트하면,
학습 중 데이터 또는 모델이 변경될 때 [75, 82] 또는 테스트 중일 때 [65, 89] 모델 성능을 향상시킬 수 있음을 발견하였다.

이러한 BN 재보정(recalibration) 기법은 다음과 같은 영역에서 유망한 효과를 보였다.

• 모델 성능 향상 [42, 85]
• 도메인 적응(domain adaptation) 및 일반화 능력(generalization ability) 개선 [54, 77]
• 소수 샷 학습(few-shot learning) 성능 향상 [21]
• 입력 노이즈에 대한 모델의 강건성(robustness) 향상 [10, 66, 79]

7. Conclusion and discussion

우리는 테스트 샘플과 훈련 데이터 간의 신경 평균을 비교하는 Neural Mean Discrepancy (NMD) 기법을 제안하여 OOD 탐지를 수행하였다. 적분 확률 측도(IPMs) 기반의 이론적 분석과 실험적 결과를 통해 NMD의 효과를 검증하였다. 알고리즘적 단순성이 극대화된 NMD는 다양한 데이터셋, 모델, 데이터 접근 환경에서 평가되었으며, 최첨단 수준의 정확도와 효율성을 달성하였다.

7.1 Limitation

NMD는 실제 OOD 데이터에 접근하지 않고도 경쟁력 있는 결과를 얻을 수 있지만(섹션 5.3 참조), 채널 감도를 학습하기 위해 픽셀 셔플링(pixel shuffling)을 이용한 인공적인 OOD 데이터가 여전히 필요하다. 대신, 사전 학습된 모델의 가중치 분포 [41, 87] 또는 그래디언트 정보 [4, 81]를 이용하여 감도를 직접 추정할 가능성이 있다. 또한, 기존 연구 [3, 56]를 활용하여 NMD 기반 OOD 탐지기의 성능을 더욱 향상할 수 있을 것으로 기대된다.

[3] Vahdat Abdelzad, Krzysztof Czarnecki, Rick Salay, Taylor Denounden, Sachin Vernekar, and Buu Phan. Detecting outof-distribution inputs in deep neural networks using an earlylayer output. arXiv preprint arXiv:1910.10307, 2019. 8, 13
[5] Andre Araujo, Wade Norris, and Jack Sim. Computing re- ´ ceptive fields of convolutional neural networks. Distill, 2019. https://distill.pub/2019/computing-receptive-fields. 3

Appendix - Lightweight OOD Detector의 모델 구조 

•  Logistic regression (LR):

binary classification을 위한 고전적인 머신러닝 모델 중 하나이다. 주어진 입력 벡터에 대해, LR 모델은 학습된 계수 벡터와 입력의 내적을 수행한 후 시그모이드 함수를 적용하여 예측 점수를 출력한다.논문에서는 LR  학습을 위해 sklearn [1]의 기본 하이퍼파라미터를 사용한다.

•  Multilayer perceptron (MLP)

논문에서 사용하는 다층 퍼셉트론(MLP)은 비선형 활성화 함수인 ReLU를 따르는 세 개의 FC layer로 구성됨, 두 번째 FC layer 이후에는 드롭아웃을 적용하며, MLP는 SGD 옵티마이저를 사용하며 MLP를  0.001의 learning rate와 0.9의 모멘텀을 가진 SGD를 사용한다.

 

논문에서  MLP가 LR보다 탐지 성능이 약간 더 우수하지만, 학습 예제 수가 제한적일 때 과적합 가능성이 더 높음을 발견했다. 

Appendix - Architecture of ConvNet

Sec. 5.1, Tab. 1에 사용된 simple ConvNet의 아래의 표와 같이 구성됨 

Appendix - Pre-trained or Un-trained Models?

Fig 3에서, 사전 학습된 ResNet-34의 NMD 벡터에서 요소들의 크기 평균을 OOD 점수로 사용하여 OOD 배치를 신뢰성 있게 구별할 수 있음을 보여준다. 이러한 예시는 사전 학습된 모델이 유효한 증인 함수(witness function)로 활용될 수 있음을 검증한다.

 

이를 바탕으로, 우리는 사전 학습된 모델 자체가 훈련 데이터 분포에 대한 충분한 정보를 포함하고 있다고 가정하는데 이는 모델이 훈련 데이터를 특징적으로 포착하도록 학습되었기 때문이다.

 가설을 추가로 검증하기 위해, 사전 학습된 ResNet-34를 학습되지 않은 ResNet-34로 교체한 후 동일한 실험을 다시 수행했다. Fig. 8 에서 볼 수 있듯이, 학습되지 않은 ResNet-34는 배치 크기가 8인 경우에도 OOD 배치를 탐지하는 유효한 증인 함수로 작용하지 못했다.

Appendix - Neural Variance Discrepancy

NVD 수식(variance 이용)

 

Sec. 5.7에서 언급한 바와 같이, Neural Variance Discrepancy(NVD) 는 활성값의 2차 통계량(second-order statistics) 을 계산하여 정의할 수 있으며,
이는 Neural Mean Discrepancy(NMD) 와 유사한 방식으로 측정할 수 있다.
특히, NVD의 두 번째 항(term) 은 BN(Batch Normalization)의 실행 평균 분산(running average variance) 으로 근사할 수 있다.

흥미롭게도, NVD 기반 탐지 모델(NVD-MLP) 는 NMD와 유사한 탐지 성능 을 달성하였다.

추가적으로 NVD와 NMD를 결합 하여 탐지 성능을 향상시키고자 하였다. 그러나, NVD와 NMD의 요소 값들이 서로 다른 크기(magnitude)를 가질 수 있기 때문에,
이를 결합하기 전에 sklearn의 표준화(standardizer) 기법 을 적용하여 각 차원의 평균을 제거하고(unit mean 제거), 분산을 1로 조정(scale to unit variance)하였다.

NVD와 NMD를 결합한 결과, 탐지 성능이 소폭 향상 되었으나, 추가적인 연산 비용(computation overhead) 이 발생하는 단점이 있었다.

Appendix - Crafting OOD Data by Pixel Permuting

Sec. 5.3에서 논의된 바와 같이, OOD 예제가 주어지지 않은 경우, in-distribution 예제의 픽셀을 무작위로 섞어 인공적인 OOD 예제 를 생성하고, 이를 탐지기의 결정 경계(decision boundary) 학습 에 활용할 수 있다.

이러한 인공 OOD 예제(crafted OOD examples) 를 사용하는 근거는, 해당 방법이 데이터셋 전반에서 높은 일반화 성능(generalizability) 을 보인다는 점이며, 이는 Sec. 5.5에서 검증되었다.

 

구체적으로, 우리는 픽셀 단위가 아닌 블록 단위(block granularity)로 픽셀을 섞는 방법 [73] 을 사용하였다.
이 방식은 하이퍼파라미터인 "변이율(mutation rate)"을 조정할 필요가 없도록 해준다.

예를 들어, CIFAR-10 이미지 에 대해,

• 이미지를 16개의 8 × 8 블록으로 나눈 후,
• 블록들의 위치를 무작위로 섞는 방식 을 적용하였다.

OOD 예제 없이 수행한 탐지 성능 결과는 Fig. 5 및 Tab. 6 에 제시되어 있다