[Change point detection][Clustering] Unsupervised Change Point Detection in Multivariate Time Series (Wu, D., Gundimeda, S., Mou, S. & Quinn, C. AISTATS 2024)

https://proceedings.mlr.press/v238/wu24g.html

Unsupervised Change Point Detection in Multivariate Time Series

 

Introduction

Non-Stationary를 모델링하는 것은 다양한 분야에 사용되나 일반적으로 어려운 문제이다. 대표적인 접근법 중 하나는 시계열을 여러 부분으로 나누고 각 부분에 관한 정상성을 가정하는 것이다. 각 나누어진 부분에 stationary model 적용하는 것은 상대적으로 쉬운 부분이지만(which is the local problem), global한 문제인 각 부분을 어떻게 나눌 것인지 결정하는 change point를 찾는 문제는 어려운 문제이다. 

Change point detection은 이 외에도 fraud detection (Murad and Pinkas, 1999), quality control (Bissell, 1969), climate monitoring (Beaulieu et al., 2012), seizure detection(발작 탐지)(Schr¨oder and Ombao, 2019) and motion transition detection(동작 변환 탐지)(Liu and Chan, 2017) 등 다양한 분야의 서브루틴으로 사용된다. 많은 연구가 이루어졌지만 여전히 아래의 문제점이 존재한다. 

 

1. 과도한 파라미터 튜닝 요구: 기존 방법들의 경우 하이퍼파라미터 조정을 필요로 하며(Aminikhanghahi and Cook, 2017; Truong et al., 2020) 적절한 값을 설정하는 것이 어렵다. 대표적으로 검정 임계값(threshold, h) 및 변화점의 개수(k)가 있다. 

2. Focus on specific change: 평균, 분산 변화 혹은 기타 통계량의 조합에서 변화가 있을 수 있으나 특정 통계 변화에 집중한 알고리즘이 많음. 

3. Addtional Statistical assumptions: CPD 방법론들은 대부분 통계적인 가정하에 방법론이 서술됨. 예를 들어 베이지안 접근법은 사전 분포에 대한 지식을 요구하며(Adams and Mackay, 2007), Hidden Markov Model 방법은 동일한 상태를 여러 번 방문해야 한다. 또 일반적으로 가정은 각 정상성 구간 내의 데이터가 IID assumption을 따른다는 것이다(Aminikhanghahi and Cook, 2017). 그러나 이러한 가정은 실제 시스템에서 비현실적일 수 있다.

4. 다변량 시계열에 관한 처리 부족: 대부분 단변량에서의 방법론을 단순히 집계하는 방식으로 사용하지만( (Bardwell et al., 2019) ), 변수들간의 상호작용(inter-dependencies)를 놓칠 수 있음

5. High Computational complexity

 

따라서 본 논문에서는 Sliding window 기반 클러스터링 방법을 통해 변화점이 있는 구간을 자동 탐색. Minimum Description Length(MDL)을 활용하여 최적의 변화점을 선택하는 방법을 제시한다. 이는 사전에 변화점 개수를 알 필요가 없으며, 유연하고 다변량 데이터에 적용 가능하다. 

제안된 방법은 두 가지 주요 단계로 구성된다:

1. 슬라이딩 윈도우 기반 모델 학습 및 클러스터링
각 윈도우에서 데이터 분포를 학습하고, 유사한 통계적 특성을 가진 윈도우를 클러스터링.
2. MDL 기반 변화점 탐색
클러스터된 분포들 간 차이를 분석하여 최적의 변화점을 탐지하는 그리디 알고리즘 적용.

1.1 Related Work for the multivariate change point detection

Modified version of Binary segmentation:

SBS(Cho and Fryzlewicz, 2015), DCBS(Cho, 2016), E-Divisive 및 E-Agglomerative(Matteson and James, 2014)

 

Multivariate version of BOCPD:

BOCPDMS (Knoblauch and Damoulas, 2018)

 

Genetic algorithm(Davis et al., 2006), Random partitions( BNB, Hooi and Faloutsos, 2019), Clustering sliding windows for IP(Wu et al., 2020 ) 등 여러 방법론이 제시됨. 다만 언급된 방법들이 Univariate에 타겟되어있는 경우가 많다는 것이 기존 연구 방법론의 한계점으로 제시됨. 

 

1.2 Background( Minimum Description Length (MDL) principle)

논문에서 사용된 MDL 원칙에 관한 설명, 자세한 내용은 Gr¨unwald, 2007 참고. 

 

MDL이란, 모델 선택을 위한 관점 중 하나로 데이터를 가장 간결하게 설명할 수 있는 모델이 최선의 모델이라는 아이디어에 기반한다(mathematical applications of Occam's razor). 이는 모델의 복잡도와, 모델을 사용한 데이터의 인코딩 길이의 합으로 정의된다. 

정보이론에서 유래된 개념임으로 엔트로피와 관련된 개념들과 함께보면 좋을듯하다 
https://secundo.tistory.com/68 (엔트로피 관련 내용)

 

D라는 데이터집합과 모델 클래스에 속하는 모델인 M이 주어졌을때, 모델 M에 관한 coding length인 CL(D|M)을 정의할 수 있다. 

이는 일반적으로 negative log likelihood로 측정(cf: entropy 개념)된다. 또한 모델 M 자체를 인코딩하는 데 필요한 CL(M) 또한 정의 가능하다. 따라서 우리는 이 둘의 합을 CL(D, M)으로 정의하며 best model을 해당 CL(D, M)의 argmin으로 정의한다. 

 

2. Problem Formulation: Change point 정의 

다음으로 Piece-wise stationarity를 가지는 시계열의 특성을 설명하고 change point detection을 위한 최적화 문제를 정의한다. 

 

1. Multivariate Time series Y

시계열 Y는 다음과 같다. 

 

이는 discrete-time의 d차원의 Markov order-p(마코프 차수:p, 즉 이전 p개의 상태에 의존하는 마코프) 시계열이라고하며 그 길이는 T라고 하자. 

 

과거 p의 history(즉 바로 직전 0에서 그 이전 p까지의)에 대해 조건부로 주어진 시계열의 joint distribution은 아래와 같이 표현가능하다. 

 

2. Chage point τi

Change point τi​는 변화점으로 해당 지점 이후에 조건부 분포가 변화하는 점이다. 수식상 이는 아래를 의미한다.

 

1. necessary condition : 𝜙𝑖≠𝜙𝑖+1 (해당 구간의 매개변수 벡터 𝜙 )
2. 변화 측정 조건: Kullback-Leibler 발산(KL divergence)이 0보다 커야 한다. 즉 단순히 모델 파라미터(모수 등)가 다르다는 것이 확률분포가 다르다는 것을 의미하지는 않는다 

2에 있어서 exponential family) 분포에서는 충분 통계량(sufficient statistics) 선형 종속일 경우, 서로 다른 매개변수 벡터가 동일한 분포를 유도할 수도 있다. 이에 대한 자세한 내용은 (Lehmann and Casella, 1998)의 섹션 1.5를 참고하라

 

- 전체 시계열의 확률 표현(Markov model)

Chain rule과 Markov property에 의하여 임의 realization(현재 주어진 값) y1:T는 임의의 history인 y1-p:0에 대하여 시간에 따라 다음과 같이 분해 가능하다(Markov and individual property, 즉 Y1:T의 확률을 모두 한번에 계산하는 것이 아니라 각각 계산 후 곱으로 표현 가능)

즉 전체 시계열 Y1:T 의 확률은 각 시점 ttt 에서의 조건부 확률의 곱으로 표현됨

 

- 변화점이 있는 경우 

변화점이 존재하는 경우 시계열은 서로 다른 구간(segment)로 나눌 수 있다. 

시계열의 Joint distribution이 Piecewise stationary이며 매개변수 공간 Φ의 벡터들로 매개변수화 되어있다고 가정하자. 

change point를 τ0=1, τ1,...,τk,τk+1=T+1 이라고 하자. 

그럼 각 segment에서는(각 변화점 사이에서는) 동일한 확률 모델 Pϕi를 사용할 수 있기에 아래와 같이 식(2)를 단수화 할 수 있다. 

 

이 변화점에서 다음 변화점까지(다음 변화점은 포함하지 않음)의 기간을 epoch라고 하자. 

이때 비연속적인 에포크에서는 동일한 모델이 반복될 수 있으며(정상 -> 비정상 -> 정상 시계열로 돌아오는것도 변화점임) 서로다른 매개변수 벡터의 개수를 ek라고 하고 이들의 집을 

라고 한다. 

 

Let's formulate the model

 

는 마르코프 차수 p및 매개변수 공간 Φ를 갖는 piecewise stationary model의 클래스이다.

 

은 변화점 개수 k, 변화점 위치 τ\, 매개변수 벡터 ϕ를 명시적으로 포함하는 piecewise stationary model  을 나타낸다.

 

 

예를 들어 Fig1(a)에서 길이 T인 piece-wise stationary linear VAR model의 relization을 보자. 

이 모델에ㅔ서 각 구간의 매개변수는

이며 각각 coefficient matrix, noise mean vector, and noise covariance matrix를 의미한다. 

 

이제 최종적으로 문제를 정의하면, 우리는 데이터에 가장 적합한  piecewise stationary model, M*을 찾는 것을 목표로 하며 아래으 Problem1을 정의한다. 

 

이때 L은 loss function이다. 이를 직접 푸는 것은 어려운 문제이기에 먼저 단일 변화점(k=1)를 찾는 문제로 단순화하고 이를 확장하여 Multiple한 change point를 푸는 것으로 확장하자. 

 

3 Estimating Single Change point 

단일 변화점 추정은 시계열이 두 개의 에포크(epoch) 만 포함하는 경우를 가정하는 것과 같다는 것을 생각하자. 

 

-기존 방법

기존 방법들은 손실함수로 log liklihood를 사용할 때, 아래의 최적화 문제를 정의하는것과 같다. 

 

하지만 위의 최적화 문제는 각  τ 에 대해 내부 최적화 문제(inner optimization)를 풀어야 하므로 계산 비용이 매우 크다(computationally prohibitive)

 

- 새로운 접근법 

 

 만일 Pϕ1  Pϕ2에 관한 좋은 근사값을 알고 있다면, 우리는 근사값 ^을 이용하여 아래와 문제를 같이 단순화 할 수 있다. 

 

이는 아래의 Theorem 1을 통해 추정된 분포가 실제 분포에 가깝고, 두 실제 분포가 충분히 다르면, 변화점 추정의 좋은 유의성을 보장할 수 있음을 보일 수 있다. 

 

위 결과를 바탕으로, 만약 추정된 분포 Pϕ^​​​ 와 두 인접한 epoch의  시작/종료 시간이 주어진다면,
이를 이용해 변화점 τ를 효과적으로 추정 할 수 있다.

그러나 여전히 다음과 같은 문제들이 남아 있다.

1. 실제 분포를 어떻게 잘 추정할 것인가?
   • 관측된 시계열 데이터를 이용하여 실제 분포에 가까운 분포를 잘 추정하는 방법이 필요하다.
2. 변화점 개수를 모를 때, 문제 1을 어떻게 해결할 것인가?(현재는 1이라고 가정하고 문제를 품)
   • 다중 변화점이 존재하고, 그 개수조차 알 수 없는 경우를 해결할 방법이 필요하다.

4. Change points Greedy Search: 논문에서 제안하는 알고리즘 

 

 

 

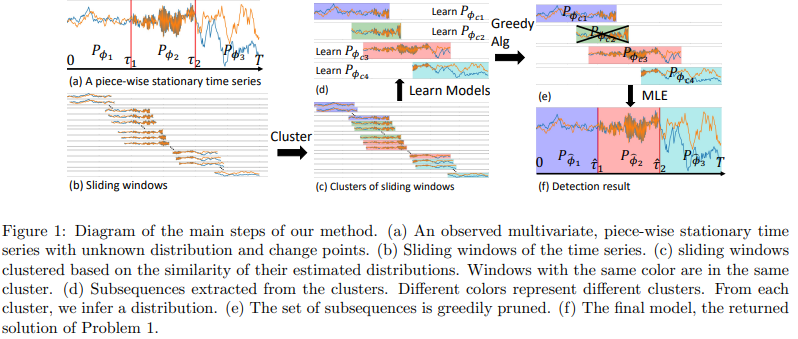
논문의 변화점 탐지 방법은 크게 다섯 단계로 이루어진다.

각 구간별 분할 및 조건부 분포 추정 → 클러스터링 →  클러스터별 대표 모델 추정→  순수 서브시퀀스(클러스터) 선택 → CP 결정

이며 Fig1을 통해 각 단계별 예시를 시각적으로 확인 가능하고, Algorithm 1은 main 알고리즘의 pseudo-code를 나타낸다. 

 

(1) Sliding winow를 통한 subsequence 생성 및 조건부 분포 추정

• 다변량 시계열 데이터를 여러 서브시퀀스(subsequences)로 분할(sliding windows)하고, 각 구간의 조건부 분포를 추정하는 과정
• Fig.1 (a)에서 첫번째 epoch에 대하여 미지의 ϕ1에 의해 매개변수가 설정됨을 확인 가능하다, 따라서 해당 구간에 해당하는 서로 다른 하위 시퀀스에 관한 매개변수를 추정한다면 해당 벡터들이 유사할 것임을 기대할 수 있다. 
• 이는 변화점이 존재하기 전까지 같은 분포에서 데이터가 생성될것이고 따라서 같은 분포에서 온 데이터라면 추정된 파라미터 벡터가 비슷할 것이라는 가정에서 유래됨 
• 따라서 각 서브시퀀스에 관한 조건부 분포를 우선 추정한다 

(2) 조건부 분포 간 유사도 계산 및 클러스터링

• 각 서브시퀀스의 조건부 분포가 얼마나 유사한지 확인후 클러스터링하여 비슷한 통계적 특성을 가진 구간들을 묶어 epoch에 가까운 하위 seqence를 얻음
• 하위 시퀀스들이 구간과 일대일 대응 관계를 갖기에 하위 시퀀스를 얻는 것은 구간에 대한 부분적인 정보를 밝히는 데 도움이 됨
• Fig. 1 (c) 에서, 클러스터링 결과를 시각적으로 확인 가능
• 클러스터링 방법:
  • 소프트 클러스터링(Soft Clustering) 방식을 사용하여 각 서브시퀀스를 여러 클러스터에 걸쳐 배정할 수 있도록 함.
  • HDBSCAN과 같은 밀도 기반 클러스터링 방법을 활용 가능.
• 동일한 데이터 생성 과정에서 나온 데이터라면 같은 통계적 특성을 가져야 함으로 해당 클러스터의 분포 추정을 통해 대표 분포를 추정가능

 

(3) 클러스터별 대표 모델 추정

• 클러스터링이 끝난 후, 각 클러스터에 대해 대표적인 확률 모델을 추정.
• 즉, 클러스터 내의 모든 서브시퀀스를 기반으로 하나의 대표적인 확률 분포 모델을 학습.
• Fig. 1 (d) 에서, 클러스터별 분포가 추정되는 것을 확인 가능 

 

다만, 모든 하위 시퀀스가 바람직한 것은 아니다(not all subsequences are desired).

일부 Window는 heterogeneous(이질적) data를 가지고 있을 수 있고, 이와 유사한 윈도우들이 병합하여 하위 시퀀스를 형성할 수도 있는데(그림 1(d)의 2번째 하위 시퀀스, 녹색) 이는 분포 추정에 도움이 되지 않는다. 

따라서 Greedy 알고리즘을 통해 올바른 하위시퀀스를 선택하고자 함.

 

(4) Greedy algorithm(pruning the sequence): 순수 서브시퀀스(Pure Subsequences) vs 혼합 서브시퀀스(Mixture Subsequences) 판별

• 클러스터링을 통해 얻어진 서브시퀀스를 가지치기하는 과
• 순수 서브시퀀스 (Pure Subsequences)
  • 대부분 같은 생성 분포에서 나온 데이터로 구성된 서브시퀀스.
  • Fig. 1 (d) 에서 1st, 3rd, 4th 서브시퀀스가 이에 해당.
  • 이러한 서브시퀀스는 상위 epoch에 대응되므로 유용한 정보 제공.
• 혼합 서브시퀀스 (Mixture Subsequences)
  • 서로 다른 생성 분포에서 나온 데이터가 포함된 서브시퀀스.
  • Fig. 1 (d) 에서 2nd 서브시퀀스가 이에 해당.
  • 이러한 서브시퀀스는 정확한 변화점을 식별하는 데 혼란을 야기할 수 있음.
  • 따라서, 혼합 서브시퀀스를 제거하는 것이 핵심.

 

(5) 변화점 및 최종 모델 결정

• 최종적으로 유지할 클러스터를 결정하고, 유지할 클러스터 간의 변화 지점을 선택한다(그림 1(e) 참고).
• 즉, 순수 서브시퀀스를 기반으로 최적의 변화점(Changepoint) τ들을 탐지.
• 이때 MDL(Minimum Description Length) 기준을 활용하여 최적의 변화점 개수 k 를 결정

 

4.1 Identifying Pure Subsequences

Greedy algorithm(pruning the sequence), 즉 순수 서브시퀀스(Pure Subsequences) vs 혼합 서브시퀀스(Mixture Subsequences) 판별하는 법을 더 자세히 알아보자. 

 

이 선택 절차는 MDL 원칙에 기반한다. 
클러스터링 결과를 처리한 후, 순서가 지정된 하위 시퀀스 리스트( S=(s1​,s2​,…,sR​) )와 이에 대응하는 모델 리스트(파라미터 리스트, ϕs=(ϕs1,ϕs2,…,ϕsR))를 가지게 된다. 
두개의 인접한 subsequence에 관하여(sliding window에 의해 일반적으로 중첩된) 둘 모두가 pure subsequence이고, 유지되어야한다고 판단되었다면, 그 사이의 change point를 찾아야 할 것이다(section 3에서 논의된바와 같이)

초기에는 모든 하위 시퀀스를 순수한 것으로 가정하고, 각 쌍 사이의 변화 지점을 지역적으로 찾는다. 이때의 모델은 다음과 같이 표현된다.

 

이제 하위 시퀀스 si를 S에서 제거한다고 가정하자. 그러면 수정된 하위 시퀀스 S'은

 

이며, 이에 대응하는 모델은 

이다.  이는 subsequence가 하나 줄어들었기 cp의 개수도 하나 줄어들어 R-2개가 되고, 변화지점을 다시 추정하면 si와 인접한 si-1과 si+1 사이의 기존 변화 지점 Ti-1,과 Ti가 제거되고, 새로운 변화지점 T'이 그 사이에 추가되기 때문이다. 

 

즉, 모델 S'에 해당하는 모델 M'은 하나의 변화지점과 경우에 따라 하나의 매개변수 벡터가 줄어들게 된다. 

이제 원래 모델 M(6)과 modified 모델인 M'(7)의 coding length를 비교할 수 있다. 

 

만약 아래와 같이 coding length가 줄어들었다면, 제거하는 것이 옳은 선택이며, 아니라면 유지해야할 것이다. 

 

즉, 하위 시퀀스 si의 점수를 두 모델의 CL 차로 정의할 수 있다. 

만일 Score가 0보다 크다면(modified coding length가 더 크다면), si는 mixture subsequence일 가능성이 높다. 반대라면 pure subsequence일 가능성이 높다. 이때 Score는 reference list S에 따라 달라진다는 것에 유의하자. 

 

 

Coding Length:

Rissanen(1998) 3.1장을 참고하면, 모델 M(k,τ,ϕ) 하에서 시계열 Y1:T의 Coding length는 negative log likelihood (NLL)로 근사 가능하다.

 

또한 모델 M의 Coding length는 식(9)와 같이 여러 부분으로 나눌 수 있다(Appendix 참고)

 

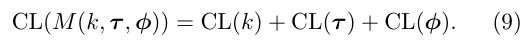
먼저 전체데이터와 모델의 M의 CL인 CL(Y1:T,M)은 식(9)에서 직접 도출 된다. 

M'에 관한 CL(Y1:T​,M′)은 

임으로, 모델 M'의 CL을 분해하면 (식 9의 유도과정과 동일)

이제 전체 부호화 길이의 두 부분을 재배열하여 하위 시퀀스 si의 점수를 계산하면 다음과 같다.

(자세한 내용은 부록 참고)

 

최종적으로 서브시퀀스 리스트 S에서 가장 가능성이 높은 혼합 하위 시퀀스 s*은 다음과 같이 정의된다. 이는 점수가 클수록 해당 하위 시퀀스가 혼합일 가능성이 높기 때문이다. 

 

Fig 2(b)를 보면 S2와 S8이 양의 점수를 가지며 S8의 점수가 가장 크기에 가장 높은 가능성을 가진 mixture subsequence는 S8이다. 

4.2 Most-likely Mixture Algorithm: Pruning the sequence 

임의의 subsequence인 s를 S에서 제거할 때, coding length의 marginal gain을 측정하는 방법을 기반으로 Most-likely Mixture Algorithm(Algorithm 2)를 제안한다.

 

우선, 모든 하위 시퀀스 s ∈ S를 포함하는 pure subsequences의 후보 list인 S를 초기화하고, 각 하위시퀀스 si의 점수(CL로 의해 유도된 수식)을 계산한다. Fig2의 예시를 보면 9개의 subseqence가 클러스터링을 통해 생성되었음을 확인 가능하고 그 score 점수도 확인 가능하다. 

그 후, 후보 리스트에서 점수가 0이 (즉, 혼합 하위 시퀀스로 판단될 가능성이 있는)인 subsequences s가 포함되어있는한 가장 가능성 높은 subsequences s*을 찾아 제거한다. 

 

Fig 2(b)를 보면 각 열은 각 클러스터를 의미한다. 

 

Fig 2(b)의 예제에서는 s2와 s8이 양수임으로 이 중 가장 큰 값을 가지는 s8을 리스트에서 제거한다. 

 

각 subsequences si를 삭제할 때마다, 남아있는 subsequences의 점수를 업데이트한다. 

1. 제거된 si의 인접 subsequence인 si−1, si+1 score를 수정

2. ϕsi = ϕsj, 즉 매개변수 벡터가 제거된 si와 동일한 sj가 존재한다면 해당 하위 시퀀스의 점수도 수정 

 

Fig 2(c)를 보면 s8이 제거된 이후 s7의 점수를 업데이트하는 것을 확인 가능하다(s9의 경우 가장 마지막 subsequence임으로 항상 −∞ 임, 즉 업데이트 불필요) 또한 s3과 s6이 동일한 매개변수를 가지지만 score 업데이트는 진행하지 않는다(why? 잘 모르겠음) . 이제 이 과정을 반복하여 모든 점수가 음수가 될 때까지 반복 수행한다. 그림 2(d)에서는 s2가 제거되고 s3의 점수가 업데이트 된 후 모든 점수가 음수가 됨으로 반복을 종료한다. 

 

 

다음 Thereom 2는 제안된 알고리즘의 이론적 보장을 제공하며, change point detection의 일관성(Consistency)에 대한 분석을 다룬다. 

우리는 변화 지점 검출 분석을 다룬 기존 연구(Bai and Perron, 2003; Truong et al., 2020)에서 사용된 가정을 따른다. 즉,

• 전체 시간 범위 T와 epoch의 길이 τi/T가 무한대로 증가한다고 가정한다.
• 윈도우 크기 W도 시간 범위 T와 함께 무한대로 증가하며, W=ωT로 표현된다(ω∈[0,1]).
• 이에 따라 생성된 하위 시퀀스는 무한한 길이를 갖게 된다.

이러한 무한 설정 아래에서, 최대 우도 추정량(MLE)의 일관성에 의해 Pϕi​​에 대하여 다음이 성리하는 Pϕi​​가 존재한다. 

이로부터 자명하게 아래의 결과를 얻을 수 있다. 

 

 

Theorem 2. (Consistency) Given two adjacent epochs with distributions Pϕ1 and Pϕ2 respectively, with change point to be τ. Consider a mixture subse quence s2 with starting time point a and ending time point b satisfying a < τ < b. Pϕs2 is learnt from data which follows π2Pϕ1 + (1 − π2)Pϕ2 , where π2 ∈ (0,1). Having adjacent subsequences s1 and s3, with Pϕsi learnt from data which follows πiPϕ1 + (1 − πi)Pϕ2 , i = 1,3 and 0 ≤ π3 < π2 < π1 ≤ 1. As sume that DKL(Pϕ1 ||Pϕs1 ) < DKL(Pϕ1 ||Pϕs2 ) and DKL(Pϕ2 ||Pϕs3 ) < DKL(Pϕ2 ||Pϕs2 ),

we can have

Proof. The detailed proof is in the Appendix

 

해당 과정으로 Pruning이 마무리가 된다면, 각 puresubsequence에 관하여 기존에 정의했던 problem 1을 푸는 것이 더욱 쉬워진다.  남은 cp의 후보군들이 각 subsequence와 1:1관계임으로 최종적인 cp만 남게 된다. 

 

 

- 계산 복잡도(Computational Complexity)

Fig 3은 시계열 길이 T에 대한 우리의 절차의 경험적 실행 시간(empirical run-time)을 나타내는 그래프이다. 실행 시간과 시간 길이 사이에는 대략적인 선형 관계(linear relation) 가 존재함을 확인할 수 있다.

실험의 세부 사항은 부록(Appendix)에 나와 있다.

5 Experiments

State of the Art Baselines:

Sliding windows (Truong et al., 2020), binary segmentation (Truong et al., 2020), dynamic programming (Truong et al., 2020), ILP method (Wu et al., 2020), BNB (Hooi and Falout sos, 2019), BOCPDMS (Knoblauch and Damoulas, 2018), SBS (Cho and Fryzlewicz, 2015), DCBS (Cho, 2016), E-Divisive (Matteson and James, 2014), and E Agglomartive (Matteson and James, 2014). Autoplait (Matsubara et al., 2014) and Fluss (Gharghabi et al., 2019)

 

ILP method는 
모든 시점 t 에 대해 변화점 후보를 설정하고, ILP 문제의 목적 함수 및 제약 조건을 적용.
ILP 솔버(예: Gurobi, CPLEX)를 사용하여 최적의 변화점 위치 및 개수 결정하고 최적화 문제를 품 단, 이는 계산 비용이 높은 단점이 있어 현실적인 데이터셋에서 활용이 어렵다(논문에서 언급됨)

 

Evaluation:

정밀도(Precision), 재현율(Recall) 및 F1 점수를 사용하여 성능을 평가, 이때 True postive는 추정된 변화지점이 실제 변화지점과 δ 거리에 있을 경우로 판정한다

Datasets:

인조(artificial) 데이터와 real-world data 모두 이용. 

 

• 인공 데이터는 (선형) 벡터 자기회귀(VAR) 모델과 (비선형) vector auto logistic regressive model에서 다양한 매개변수 변화에 대한 민감도를 평가하는 데 사용된다.
• 실제 데이터는 다음과 같은 데이터 세트를 사용한다.
  • Bee Dance (Oh et al., 2008)
  • HASC (Human Activity Sensing Consortium) (Ichino et al., 2016)
  • 실내 점유 데이터(Occupancy) (Candanedo and Feldheim, 2016)
  • MoCap Lab (모션 캡처 연구소 데이터)
•  Bee dance (Oh et al., 2008): The time series corresponds to bee movement trajectories captured by the camera. We used six time series, each with dimension d = 3 and with an average time length T ≈ 600. Fig. 7(a) shows an example time series. Each timestamp is labeled with one of the states: turn right, turn left, and waggling. The change points are timestamps when the state transition occurs.
• HASC (Ichino et al., 2016): Human motion acceleration data. We used 50 time series (the first 50), each with dimension d = 3 and an average time length T ≈ 9000. Fig. 7(b) shows an example time series. The timestamps of different phases of motion, like walking, running, etc., are recorded. The change points are when the motion changes. 
• Occupancy (Candanedo and Feldheim, 2016): The data contains information about temperature, humidity, light, CO2, and humidity ratio in a room. The dataset contains one time series with dimension d = 5 and time length T = 2665. Fig. 12(b) shows the time series. Each timestamp is labeled either as being occupied or empty. We ignore the anomalous phases with less than ten timestamps and consider the true change points are at t = 195, 1044, 1371, 1400, 1674, and 2479.
• MoCap: Human motion sensor data1. We used two time series, each with dimension d = 4 and an average time length T ≈ 11,000. Fig. 8 shows the two time series. The dataset does not have labeled ground truth. Instead, it provides recorded videos of the participant’s motions. We examine the video to check whether the change points identified by Alg. 1 is meaningful or not.

 

 

Clustering Algorithm and Window Size:

이번 연구에서는 특정 클러스터링 절차를 제안하지 않으며, HDBSCAN (McInnes et al. 2017)을 사용하여 클러스터링을 수행한다. HDBSCAN의 장점 중 하나는 사전에 클러스터 개수를 지정할 필요가 없다는 점이다.

 

윈도우 크기(Window Size)는 제안된 방법의 하이퍼파라미터이다.

• 우리는 도메인 전문가가 도메인 지식에 따라 적절한 윈도우 크기를 선택할 것을 권장
• 실험에서는 여러 윈도우 크기 범위를 탐색한 후, 최소 MDL 점수를 가지는 윈도우 크기를 선택함
• 윈도우 크기에 대한 민감도 분석 결과는 부록(Appendix)에서 확인할 수 있다

5.1 Artificial Data:

 

앞서 밝힌것 처럼 인공 데이터는 (선형) 벡터 자기회귀(VAR) 모델과 (비선형) vector auto logistic regressive model로 구성되어있음. 이제 제공된 인공 데이터에 각 CPD모델을 사용하여 분석한 결과를 보자. 

 

 

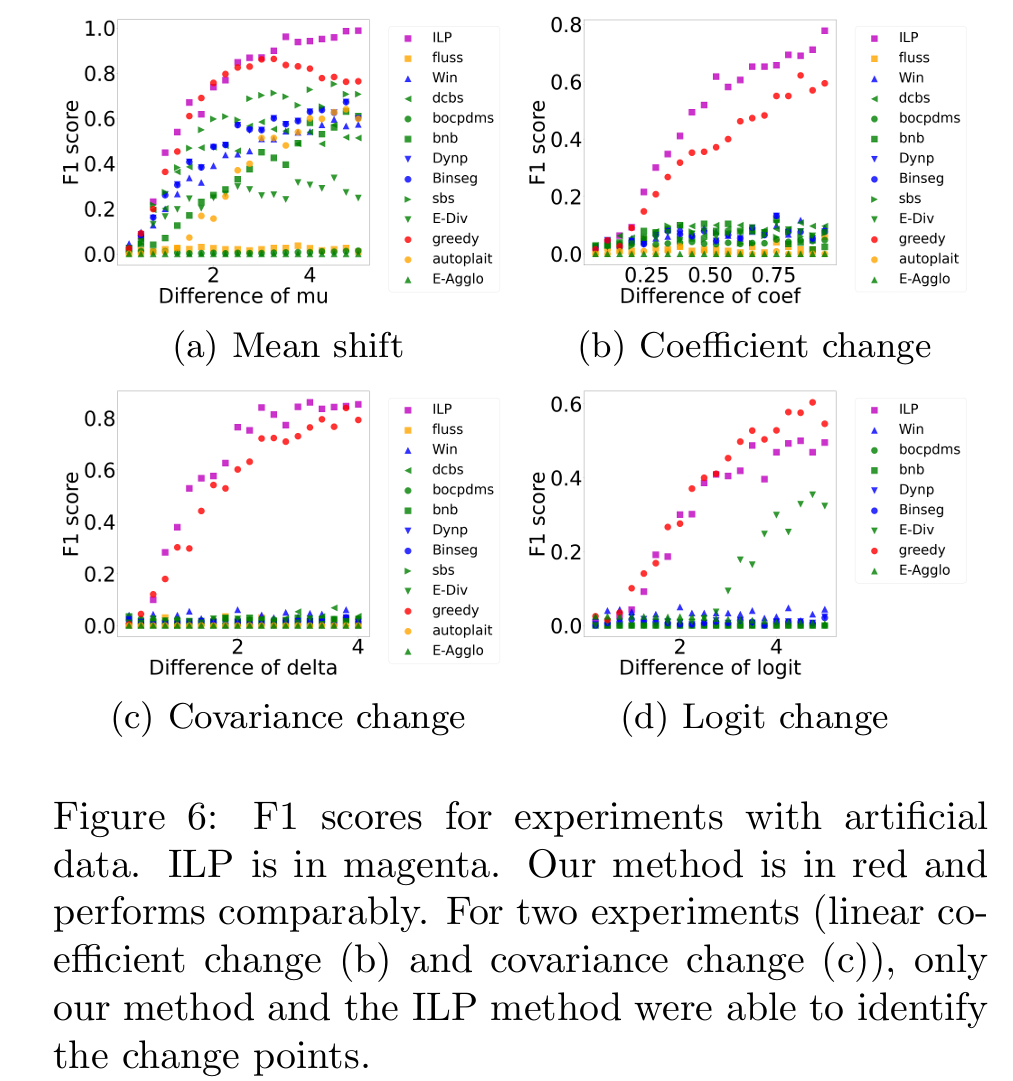
Fig 6은 인공 데이터를 사용한 실험에서의 F1 score를 보여준다. 각 하위 크래프는 두 epoch ϕ1과 ϕ2 사이의 파라미터 벡터간 다른 변화 유형( (a) Mean shift,  (b) Coefficient change, (c) Covariance change, (d) Logit change) 별 결과를 보인다. 

y축은 F1 점수를 나타내며, 점수가 높을수록 성능이 우수함을 의미하고. x축은 변화하는 통계량의 차이를 나타낸다.

 

붉은 원으로 표시되는 greedy가 본 논문에서 제시하는 알고리즘이다. 

단변량 방법인 ILP(Wu et al., 2020)는 마젠타색 사각형으로 표시되었고. 세 가지 기존 변화점 탐지 기법은 파란색 마커로, state of-the-art change point detection method는 녹색 마커로 표시되었다. Semantic segmentation methods는 주황색 마커로 표시되었다. 

 

결과는 아래와 같다. 

 

우선 모든 실험에서 ILP와 greedy방법론은 거의 동일한 성능을 보였고, 이는 다른 모든 방법들 보다 우수한 F1 Score를 의미한다. 

특히  선형 VAR 계수 변화 탐지 (Fig. 6(b)), 공분산 변화 탐지 (Fig. 6(c))에서는 오로지 두 방법론 만이 안정적인 CP탐지를 보임. 

Fig 4의 b를 보면 시각적으로도 그 변화를 확인할 수 있지만, 다른 기존 방법들은 잘 탐지하지 못하는 것을 확인 가능하였다.

Fig 5의 경우 시각적 변화가 명확하지는 않지만, greedy가 변화를 여전히 안정적으로 탐지함을 확인 가능했다. 

logit change에서는 E-div만이 logit이 큰 경우 일부 변화탐지가 가능했지만, greedy와 ILP방법보다는 그 성능이 떨어지는 것을 확인 가능하다. 

 

5.2 Real data

 

논문에서는 실제(real-world) 데이터셋을 활용하여 제안된 변화점 탐지 방법을 평가하고, 기존 방법(베이스라인)들과 비교하였습니다. 평가는 F1 Score, Precision, Recall을 기준으로 이루어졌으며, 주요 결과는 Table 1, 2에 요약되었습니다.

 

 

BNB, E-Divisive, BOCPDMS, SBS, Autoplait, Fluss와 비교만 수행하였음, 이는  (a) 다중 변화점(k > 1)을 처리하지 못했거나, (b) 가장 작은 실제 데이터 세트에서도 실행 시간이 너무 길었거나, (c) 두 가지 문제를 모두 가지고 있었기 때문입니다.

 

가장 높은 F1 점수와 최고 점수 대비 5% 이내의 점수는 굵게 표시하였고. 결과적으로, 더 큰 마진(δ)을 허용한 경우에도 우리 방법이 모든 실제 데이터 세트에서 다른 모든 방법보다 우수한 성능을 보였음을 확인 가능함. 

Fig 7을 보면

a. 벌 춤(bee dance) 데이터 6(파란색)과 다양한 방법으로 탐지된 변화점(수직 빨간선)을 보여줌. 첫 번째, 두 번째, 세 번째 패널의 시계열 데이터는 벌 춤 데이터에서 각각 x, y, sin(θ)에 해당.

첫 번째부터 세 번째 패널까지는 논문이 제안한 greedy가 탐지한 변화점이 표시되어 있습니다. 네 번째 패널부터 마지막 패널까지는 E-Divisive, SBS, BOCPDMS, BNB, Autoplait, Fluss 방법이 탐지한 변화점을 수직 빨간선으로 표시

b. 첫 번째 패널은 3D 시계열 데이터와 greedy 이 탐지한 변화점을 보여줍니다. 두 번째 패널부터 마지막 패널까지는 SBS, BNB, Autoplait, Fluss 방법의 탐지 결과를 표시

 

(a)에서 t = [137,169] 및 [223,261]과 같은 강한 변동이 있는 구간은 벌이 흔들춤(waggling)을 수행하는 시기를 나타내는데 이는 논문에서 제안한 변화점이 정확히 벌의 움직임 전화과 일치함을 보여준다. 

 

(b)의 HASC data는 첫 번째 패널에서 여러 개의 뚜렷한 활동 단계가 나타나고, 오른쪽에서 왼쪽으로 활동 순서는 계단 내려가기, 걷기, 깡충 뛰기, 조깅, 걷기, 정지, 계단 올라가기를 나타냄. 첫 번째 패널의 세로선으로 표시된 논문에서 제안한 방법의 탐지 결과는 모든 전환점을 성공적으로 식별함을 보여줌. 

 

마지막으로 Fig 8에서 MoCap 데이터의 예제와 알고리즘 1이 탐지한 변화점을 보여줍니다. Fig 8 (a)에서는 subject 86 trial2 에서 모든 주요 동작 전환이 성공적으로 탐지되었음을 보이고, 8(b)에서는 첫 번째 동작 단계 변화(걷기 → 쪼그려 앉기, 즉 8(b)에서 1단계 → 2단계)에서 두 개의 근접한 변화점이 탐지함을 확인 가능하다.  또한 8(b) 캡션에서 설명된 주요 변화 외에도,  t=755 및 t=8796에서 추가적인 두 개의 변화점을 탐지했는데 비디오를 확인한 결과, 해당 시점에서 피험자가 크게 우회전하는 동작을 수행한것임을 확인 가능했다. 

6 Conclusion 

슬라이딩 윈도우 클러스터링을 기반으로 한 새로운 비지도 학습 변화 탐지 방법을 제안한 본 논문은 광범위한 파라미터 튜닝이 필요하지 않고, 확장성이 뛰어나며 다변량 시계열 데이터를 처리하도록 설계되었다. 또한 제안된 방법에 대한 이론적 분석을 제공하며, 실제 데이터에서 의미 있는 변화점을 효과적으로 탐지할 수 있음을 입증하는 다양한 실험을 수행 입증하였다.

Appendix 1 Clustering Models from sliding window

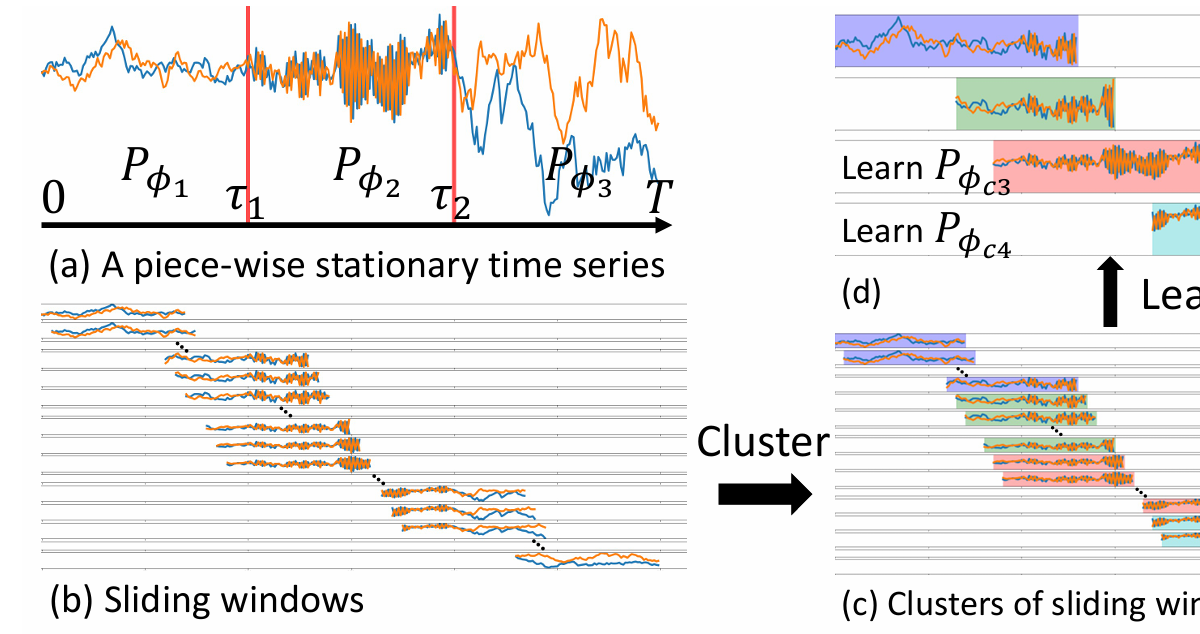
Fig 1 일부 자름

 

처음에는 각 클러스터가 기본 모델에서 하나의 에포크에 해당할 것이라고 기대할 수도 있다. 예를 들어, Fig 1(a) 에서처럼 기본 에포크가 3개라면, 3개의 클러스터가 생성될 것이라 예상할 수 있다.

 

그러나, Section 4에서 논의했듯이, 일반적으로 이러한 기대는 충족되지 않습니다(mixture subsequence가 존재). Fig 1(c)를 보면, 원래의 에포크 1과 에포크 2에 해당하는 윈도우들이 하나의 클러스터(초록색)로 그룹화된 것을 확인 가능하다. 하지만, 에포크 2와 에포크 3이 겹치는 부분에서는 별도의 클러스터가 형성되지 않았다. 따라서, 단순히 모든 클러스터를 각각 하나의 에포크와 매칭하는 방식은 적절하지 않다.

 

Fig 2일부 자름

 

또한, 동일한 조건부 분포가 비연속적인 여러 에포크에서 반복된다면, 이러한 비연속적인 에포크에서 나온 윈도우들이 하나의 클러스터로 묶일 수 있다. 실제 데이터 세트에서 이러한 현상을 보여주는 예시는 Fig 2(b)로, 여기서 세 번째 클러스터는 서로 분리된 세 개의 구간에서 나온 윈도우들로 구성되었다.

 

우리는 이후의 절차를 설명하기 위해 다음과 같은 용어와 표기법을 정의한다.

• nC: 클러스터의 개수
• Cᵢ: 클러스터 i에 속하는 윈도우들의 집합
• Cᵢ = ∪wⱼ ∈ Cᵢ일때, wⱼ: 클러스터 i에 해당하는 모든 윈도우가 포함하는 타임스탬프의 집합

예를 들어, Fig 9에서 첫 번째 클러스터(C₁)는 처음 26개의 윈도우(ω₁, ω₂, …, ω₂₆)를 포함한다.
윈도우 크기 W = 30, stride = 1인 경우,

 

각 클러스터 Cᵢ 에 대해, 해당 클러스터의 모든 타임스탬프 데이터를 이용하여 모델을 적합(fit)하고, 이를 다음과 같이 표현한다. 

클러스터 Cᵢ 전체 데이터를 이용하여 적합한 모델(ϕCᵢ)은, 해당 클러스터 내 개별 윈도우에서 적합한 모델(ϕw)보다 더 정확할 것으로 예상되며, 다음 단계에서는, 이렇게 적합된 모델들 {ϕCᵢ}을 이용하여 어떤 클러스터를 유지할지(즉, 에포크로 간주할 클러스터를 선택) 결정하고, 각 클러스터 간 변화점(change points)을 함께 추정하는 방법을 제안한다.

 

Appendix2 Estimating Change points from the clustered models

비연속적인 에포크가 동일한 파라미터를 가지는 경우, 논문에서 제안한 방법은 비연속적인 에포크에서 나온 윈도우들이 동일한 클러스터로 그룹화 될 수 도 있다. 

 

예를 들어 Fig2(b)를 보면 인간 동작 데이터의 클러스터링에서 두개의 walking state의 일부 타임스탬프가 동일한 클러스터에 속한 것을 확인 가능하다(각 열이 클러스터를 의미하고 특히, 세 번째 클러스터(그림 2(b)-(d)에서 세 번째 행)는 subsequence s3,s6,s8로 구성되며, s3 과 s6​ 은 걷기(walking) 동작에 해당하고, s8 은 의미 없는(spurious) 구간) 

 

subsequence 라는 용어는 논문에서 동일한 클러스터 내에서 최대 길이를 가지며 연속적인 윈도우들의 집합을 의미한다. 각 클러스터에 Ci에 관하여, ri는 클러스터 Ci의 subsequence의 개수, Si = {si,1,si,2,··· ,si,ri }는 클러스터 Ci를 최소한으로 covering할 수 있는 집한을 의미한다. 만일 클러스터 Ci가 하나의 서브스퀀스로 구성된다면 ri=1이다. 

 

Fig9는 슬라이딩 윈도우들의 pairwise similarity와 클러스터링 결과를 보여준다. 

이 시계열 데이터에는 변화점이 t=50t = 50t=50 에 존재하며, 결과적으로 세 개의 클러스터가 탐지되었다. 

이 특정 예제에서는, 각 클러스터가 하나의 서브시퀀스만을 유도한다, 즉, 한 클러스터가 여러 개의 분리된 서브시퀀스를 포함하지 않고, 연속적인 하나의 구간만을 포함한다는 뜻이다. 

 

주어진 변화점을 고려할 때, 서브시퀀스는 두 가지 유형으로 나누어짐:

1. 순수 서브시퀀스(Pure Subsequence):
   • 서브시퀀스의 대부분이 하나의 에포크(epoch)에서 온 경우
   • 예)
     • 첫 번째 서브시퀀스 (1,2,…,55)
       • 대부분의 데이터가 첫 번째 에포크 Y0:49 에서 유래 → 순수 서브시퀀스
     • 세 번째 서브시퀀스 (46,47,…,100)
       • 대부분의 데이터가 두 번째 에포크 Y50:100 → 순수 서브시퀀스
2. 혼합 서브시퀀스(Mixture Subsequence):
   • 서브시퀀스가 서로 다른 두 개 이상의 에포크에서 데이터를 포함하는 경우
   • 예) 두 번째 서브시퀀스 (31,32,…,75)
     • 첫 번째 에포크( Y0:49​ )와 두 번째 에포크( Y50:100)의 데이터가 혼재되어 있음 → 혼합 서브시퀀스

이후 모든 서브시퀀스를 시작 시간을 기준으로 시간상 정렬한다. Fig 2(b)가 그 예시이다. 

순수 서브시퀀스(Pure Subsequences)는 에포크를 나타내므로, 이를 이용하여 변화점을 추정할 수 있으며, 위에서 언급한 것처럼 Greedy method를 통해(using coding length) 이를 해결함. 

Appendix 3 Coding length and Score 

정수 k를 인코딩하는데에는 log2k 비트가 필요하다, 따라서 

 

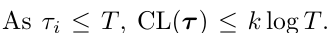
이다. 

 

다음으로 k개의 고유한 파라미터 벡터 ϕ만 인코딩하면 되기에, CL(ϕ)은 아래와 같이 정의됨(각 파라미터 벡터의 인코딩의 합)

 

각 파라미터 벡터 ϕi를 최대우도추정(Maximum Likelihood Estimation, MLE)으로 추정하기 위해 사용된 관측값 개수를 ni​ 라고 하면, 각 파라미터는 1/2 * log2ni로 인코딩 할 수 있음이 알려져 있음(Grünwald, 2007)

따라서 CL(ϕ)는 다음과 같이 카디날리티를 이용해서 계산가능하다. 

 

Score에서 

 

첫번째 항은 아래와 같이 근사할 수 있다. 

• ai​ 와 bi​ 는 서브시퀀스 si​ 의 시작 및 종료 시점
• 식 (11)은 변화점 τ′의 로컬 추정값을 기반으로 도출됨
• 탐욕적(greedy) 탐색을 수행하는 과정에서, 첫 번째 및 마지막 서브시퀀스는 항상 "순수 서브시퀀스(Pure Subsequences)" 로 간주, 즉 해당 점수는 고정값 −∞로 설정

이제 식 9와 10을 이용

 

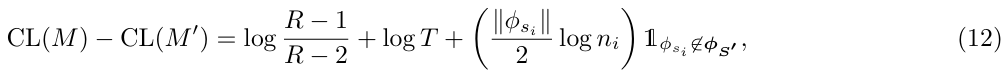
여기서,

• ni는 파라미터 ϕsi 를 추정하는 데 사용된 샘플 개수
• 마지막 항 1~은 ϕsi가 다른 서브시퀀스에서 재사용되지 않을 때 1을 반환
• 즉, 다른 서브시퀀스에서 사용되지 않는 파라미터 벡터는 추가적인 CL을 절약(save)함