[Time series][CPD] Neural network-based CUSUM for online change-point detection (by Tingnan Gong, Junghwan Lee, Xiuyuan Cheng, and Yao Xie)

https://arxiv.org/abs/2210.17312

Neural network-based CUSUM for online change-point detection

이전 논문 

https://par.nsf.gov/servlets/purl/10434229

 

Check point

1. CUSUM 문제, 즉 change point detection 문제를 분류(Classification)문제로 변환

변환의 이론적 근거가 잘 정리되어있음. 

2. Online change point detection 방법론임 

3. Semi - Supervised Model임(정상 label(정상 시계열)을 미리 정해두고 모델을 이용해야함)

* 하나의 변화점이 감지된 후, NN-CUSUM을 초기화하여 새로운 변화점을 탐지할 수 있도록 해야한다는 단점이 있음(multi change point detection으로 하려면) 첫 번째 변화가 감지되면 누적된 통계량을 초기화(reset)하는 식으로 사용해야할듯

Abstract 

Change point Detection은 Sequential 데이터(연속적)에서 데이터 분포의 급격한 변화를 감지하는 것으로, 이는 통계학과 머신러닝에서 중요한 문제이다. CUSUM은 재귀적 계산으로 인한 효율성과 일정한 메모리 요구량과 통계적 최적성질을 갖추기에 대표적인 통계적인 온라인 CPD 방법론이다. 다만 CUSUM은 변화 전후의 정확한 분포를 알아야 하지만, 변화 후 분포는 이상치나 새로운 패턴을 나타내므로 사전에 알기 어려운 경우가 많다. 따라서 실제 데이터와의 모델 불일치가 발생하면 기존 CUSUM의 성능이 저하될 수 있다. 우도비 기반 방법(liklighood ratio-based mehtods)은 고차원 데이터에서 어려움을 겪는 반면, 신경망은 계산 효율성과 확장성을 갖춘 변화점 탐지 도구로 떠오르고 있다. 본 논문에서는 온라인 변화점 탐지를 위한 신경망 기반 CUSUM(NN-CUSUM)을 소개한다. 또한, 훈련된 신경망이 변화점 탐지를 수행할 수 있는 일반적인 이론적 조건과 목표 달성을 위한 손실 함수에 대해 논의한다. 나아가 Neural Tangent Kernel 이론과 결합하여 평균 운행 길이(ARL) 및 기대 탐지 지연(EDD)과 같은 표준 성능 지표에 대한 학습 보장을 확립한다. NN-CUSUM의 성능은 합성 및 실제 데이터를 활용한 고차원 데이터 변화점 탐지를 통해 입증된다. 

 

1. Introduction

연속된 데이터에서 분포 변화를 빠르게 탐지하는, Change point detection 문제는 통계학과 머신러닝에서 주요한 문제 중 하나이다. 이는 적시에 탐지하는 것으로 손실을 최소화하는데 필수적이다. 예를 들어 생산라인의 통제 불가능 상태를 감지하는 등에 사용 될 것이다, 이외에도 변화점 탐지는 유전자 매핑 [23], 센서 네트워크 [21], 뇌 영상 [5], 소셜 네트워크 분석 [20, 15] 등 다양한 분야에 적용될 수 있다. 

 

현대의 방대한 데이터는 이전보다 더 복잡한 차원과 분포를 가진다는 특징이 있다, 하지만 기존 방법론의 가정은 고차원성과 순차적 데이터의 복잡한 시공간 의존성을 포함한 새로운 문제를 해결하기에 지나치게 제한적이다. 이를 해결하기 위하여 다양한 방법이 제시되었다. 

딥러닝 아키택쳐를 이용하여 Density estimation과 change point detection에 사용하려는 방법론이 존재하였다. 

또한 Moustakides와 Basioti [19]는 신경망을 활용하여 우도비 또는 그 변환의 적절한 추정값을 학습하는 프레임워크를 제시하였고 이를 변화점 탐지 및 가설 검정에 활용하려는 방법을 연구하였다, 

온라인 신경망 학습을 통한 CPD는 최근 ONNC 및 ONNR [10]를 통해 이루어 졌으며, 이는 분류 및 회귀를 위한 신경망을 순차적으로 적용하여 현재 데이터 배치를 직전 배치와 비교하는 방법으로 이루어졌다. 단, ONNC 및 ONNR은 슈하트(Shewhart) 관리도 유형(과거 정보를 누적하지 않고 짧은 메모리만 활용하는 방식)으로 볼 수 있으며, 이는 CUSUM 알고리즘(재귀적 계산을 통해 과거 모든 정보를 누적하는 방식)과는 차이가 있다. 일반적으로 슈하트 관리도는 작은 변동을 감지하는 데는 한계가 있지만 CUSUM은 작은 변동에도 민감하여 점근적 최적성을 갖는 것으로 알려져 있다. 

또한 기존 연구들은 알고리즘의 이론적인 근거를 제시하지 않아 본 연구에서는 일반적인 손실 함수를 고려하여 기존 연구를 확장하고 광범위한 수치 실험과 함께 이론적 근거를 제시한다. 

 

또한 Automatic Change-Point Detection in Time Series via Deep Learning에서도 신경망 학습을 기반으로 오프라인 CPD 방법과 오류를 정량화하는 이론을 제시하였으나 본 논문의 NN-CUSUM은 Online CPD라는 점에서 차이를 가진다. 

 

본 논문의 NN-CUSUM 방법론의 시작점은 온라인 변화점 탐지를 신경망이 강점을 가진 분류 문제로 변환하는 것이다. 변화 전후 분포와 로그 우도비의 명시적 형태를 알 수 없는 상황에서, 신경망의 학습 손실은 변화 전후 분포 간의 실제 로그 우도비를 근사하는 데 유용하게 활용될 수 있다. 나아가, 신경망의 손실을 CUSUM 재귀 과정과 결합하여 활용한다. 이후  제안된 알고리즘의 평균 운행 길이(ARL) 및 기대 탐지 지연(EDD)에 대한 통계적 성능 분석을 제시하며, 정지 시간(stopping time) 분석과 신경 접선 커널(Neural Tangent Kernel, NTK)을 통한 신경망 학습 분석을 결합한다

 

2. Preliminaries

관찰되는 시계열 시퀀스는 특정 시점 k에서 변화점이 발생할 수 있으며 아래의 가설 검정 문제로 CPD를 수식화 할 수 있다. 

 

또한 변화 이전(pre-change) 데이터, 즉 Reference Sequence가 f0​ 분포 하에서 충분히 제공되어, 관심 있는 변화 이전 통계량(pre-change statistics)이 수렴할 수 있다고 가정한다(즉 데이터가 충분히 많아서 통계적 특성 모수 등을 충분히 추정가능). 

 

CUSUM (Cumulative Sum) 절차는 계산적으로 효율적인 재귀적 방법으로 널리 사용되며 아래와 같이 정의되며 해당 값이 임계값 b를 넘을 경우 change point가 포착된다.

 

변화 후 분포 f1는 일반적으로 알려져 있지 않으며, 가정한 분포가 실제 분포와 차이가 있을 경우 CUSUM의 성능이 저하될 수 있다.

미지의 분포를 따르는 데이터를 Online sequence라고 한다. 

 

또한 아래의 τ를 Stopping time, 정지 시간이라고 정의한다. 이는 CPD 알고리즘에서 정의한 통계량이 임계값을 넘은 시점을 의미한다.

데이터셋 명칭 구분

논문을 읽으면서 가장 개인적으로 햇갈렸던 부분이 데이터를 분리하고 구분하는 과정들이었다. 따라서 해당 내용을 우선 한번 정리하고 넘어가자. 

데이터	설명	라벨(y 값이 0인경우 정상데이터)	학습에서 저장 위치
Reference Sequence	변화가 없는 정상 데이터	y=0	Training Stack / Testing Stack
Online Sequence	실시간으로 들어오는 데이터	y=1	Training Stack / Testing Stack
Train Data	신경망 훈련용 데이터	y=0 (Reference), y=1 (Online)	Training Stack
Test Data	변화 탐지용 데이터	y=0 (Reference), y=1 (Online)	Testing Stack
Online Train Data	실시간 데이터 중 신경망 훈련에 사용	y=1	Training Stack
Online Test Data	실시간 데이터 중 변화 탐지에 사용	y=1	Testing Stack

 

3. NN - CUSUM 

NN-CUSUM은 참조 시퀀스과 온라인 시퀀스를 순차적으로 입력받는다. 학습과정에서 변화점 탐지 문제를 Binary Classification 문제로 변환한다. 

 

• 시간 지수 i에서, 참조 시퀀스의 데이터에는 레이블 y=0을 할당하고, 온라인 시퀀스의 데이터에는 레이블 y=1을 할당한다.
• 이후, 신경망에 라벨이 부착된 데이터를 입력하고, 특정한 로지스틱 손실 함수 (예: [6])를 사용하여 학습을 진행한다.
• 학습이 완료된 후, 신경망은 참조 및 온라인 시퀀스의 각 데이터 포인트에 대해 로지스틱 손실값을 계산, 해당 값의 차이를 Sequential Statistics로 사용한다.

해당 수식에 관한 설명은 차후 진행

 

Figure 1: NN-CUSUM 절차의 개요

Figure 1은 NN-CUSUM의 절차의 개요로 이는 시간 t(왼쪽)에서 t+1 (오른쪽)로 진행되며, 아래와 같은 과정을 따른다.

 

1. 최신 스트리밍 데이터 배치
스트리밍 데이터(label y = 1로 처리)에서 최신 배치(batch)가 모델에 들어오면, 훈련 스택(training stack) 과 테스트 스택(testing stack) 으로 나누어진다(이때 훈련 및 테스트 스택의 크기를 일정하게 유지하기 위해 가장 오래된 샘플은 제거된다)

2. 모델 학습
신경망 업데이트이전 시점 t에서 사용하던 신경망을 상속하여(이어서 학습한다는 뜻), 새로운 훈련 스택 데이터를 이용해 확률적 경사 하강법(Stochastic Gradient Descent, SGD) 으로 한 번의 학습(one-pass)을 수행하여 신경망을 업데이트한다.

3. 통계량 계산
업데이트된 신경망을 사용하여 새로운 테스트 스택 데이터에서 검정통계량을 계산한다. 참조 샘플(label y=0)은  완전히 병렬적으로 생성된다. 단 모든 과정에서 스택 크기는 하이퍼파라미터로 존재한다. 

 

Train Test 과정에 관해 보다 자세히 알아보자. 

3.1 Training

NN training은 기본적으로 신경망의 파라미터 θ의 SGD 업데이트를 통해 이루어진다. 그림 1에서 확인했듯이, Train stack은 도착 데이터 스트림에서 [t-w, t] 윈도우 내에서 여러 미니배치 데이터로 이루어져 있다. 윈도우 내에서 α비율의 샘플을 훈련에 사용하고, 1−α 비율의 샘플을 테스트에 사용한다. 이는 각각 크기가 이는 각각 크기가 αw인 Online Train 데이터셋(X~tr)과 (1−α)w인 Online Test 데이터 셋(X~te)을 생성하며 α∈(0,1) 이다. 

 

훈련이 진행됨에 따라 슬라이딩 윈도우는 stride s만큼 이동하고  s의 절반은 train stack에 나머지 절반은 test stack에 배치되며 online sequence는 1, reference sequence는 0으로 라벨링 된다. Referecne Sequence는 reference sample에서 무작위로 추출되어 업데이트 된다. 

 

ϕ(x,θ)가 신경망 함수라고 할 때, 학습 과정은 아래와 같은 일반적인 loss function을 최소화하는 방식으로 수행된다.

신경망  함수는 윈도우 내에서 도착 샘플(stride가 이동하면서 추가되는 샘플, X~tr)과 참조 샘플(Xtr)의 합집합인 아래의 훈련 데이터 세트를 이용한다. 

 

위의 그림에서 언급된것 처럼 X가 tr즉 train 샘플이면 아니면 0으로 라벨링 된다. 

손실함수는 Mean loss로 정의되며 이때 샘플 별 손실함수인 l()은 여러가지 선택이 가능하다. 

 

논문에서는 아래의 3개의 Loss function을 제시한다. 

 

1. 로지스틱 손실 함수:

 

로지스틱 loss function은 global minimizer가 로그 density ratio를 제공한다는 점에서 창안하여 선택되었다. 

 

확률 밀도 함수 f0와 f1을 고려할 때 polulation loss는 아래와 같이 정의된다. 

여기서 l은 φ의 peturbation과 관련하여 보면 convex임을 확인 가능하며 argmin = log(f1 / f0)임을 알 수 있다. 

그럼으로

임을 알 수 있고, 해당 값이 0이되는 지점이 e^φ = f1/f0 이고 이것이 population loss의 전역 최소값임을 알 수 있다. 

[19]에서도 이와 유사한 접근을 이루었으며 특정 손실함수에 따라 신경망을 훈련하는 것이 이론적으로 log-likelihodd 임을 보였다. 

[19] George V Moustakides and Kalliopi Basioti. Training neural networks for likelihood/density ratio estimation. arXiv preprint arXiv:1911.00405, 2019

 

2. l2 loss(Mean squared Error)

3. MMD test statics 

로짓 손실의 선형화된 버전(linearized version of the logit loss)은 MMD 검정 통계량(MMD test statistic) [7]을 참고하여 아래와 같이 정의된다. 

최종적으로 확률적 경사 하강법(SGD)을 사용하여 손실 함수 (2)를 최소화하는 훈련이 각 윈도우 Dtr에 대해 독립적으로 수행된다고 가정한다. 시점 t에서 훈련된 신경망의 매개변수를 θt로 나타낸다. 실제 구현에서 신경망 매개변수 θ 는 초기 시점에 설정된 후, 확률적 경사 하강법(SGD) (예: Adam [11])을 사용하여 슬라이딩 윈도우 내의 훈련 샘플 배치를 통해 업데이트 되며, 새롭게 도착한 데이터는 w/s 단계 동안 stack에서 유지되며 매 k단 계마다 훈련에 사용된다. 따라서 각 데이터 샘플은 (w/s)/k 번 훈련에 사용되며 이는 효과적인 epoch 수와 동일한 하이퍼파라미터로 해석 가능하다.

 

3.2 TEST 

각 시점 t에서 훈련된 모델은 테스트 함수 g(x)를 제공한다.

 

• Logistic loss 및 ℓ2 loss 의 경우, g 함수는 다음과 같이 설정된다: 

• MMD 손실 의 경우,  함수 g는 섹션 4.3 에서 구체적으로 정의되며, 다음과 같은 형태를 가진다:

 

이때 γ > 0 은 learning rate이다. 

 

Online 탐지를 위하여 테스트 윈두우 Xte와 X~te에 관한 샘플 평균을 계산하며 이는 다음과 같이 정의된다. 

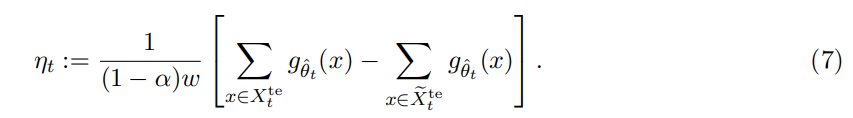
(1−α)∈(0,1)는 테스트에 사용되는 윈도우 내 데이터의 비율을 나타낸다. 따라서, αw 개의 데이터가 훈련 스택을 업데이트하는 데 사용된다. 

3.3 NN-CUSUM

초기값 S0= 0에서 시작하여 CUSUM 통계량은 다음과 같이 계산된다. 

 

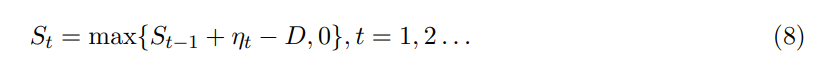
여기서 D >= 0은 작은 상수(drift)이며 변화 발생 이전에는 drift항의 기대값이 음수가 되고(즉 S가 0), 변화 이후에는 양수가 되도록 한다. 실제 구현에서는 ηt를 일정한 간격 s 마다 계산하며 s, 즉 stride는 스트림 데이터(batch loading)의 미니배치 크기 를 의미하며 양수의 정수값이다. 극단적인 경우 s=2로 설정하면 미니배치를 반으로 나누어 스택으로 분할하고, s=w인 경우 중복되지 않는 데이터를 사용 가능하다. 

 

위의 Fig 2는 힉스 보존(Higgs boson) 신호의 순차적 탐지에서 NN-CUSUM 테스트 통계량 St의 샘플 궤적을 보여준다. 이는 빨간색 점선에 해당하는 change point를 적절한 임계값을 통해 잘 감지하면 변화가 발생한 직후 신속하게 탐지할 수 있음을 보여준다.

4. Theoretical analysis

알고리즘을 설계한 근거와 변화점을 탐지할 수 있는 이유를 알아보자.

 

아래에서는 기대값(expectation)을 나타내는 기호로 다음을 사용한다:

• E0​: 변화가 발생하지 않은 경우의 기대값. 즉, 모든 데이터가 독립적으로 동일한 분포 f0​ 를 따를 때의 기대값.
• E1​: 변화가 최초로 발생한 시점 이후의 기대값. 즉, 모든 데이터가 독립적으로 동일한 분포 f1​ 를 따를 때의 기대값.

4.1 Why this works?

- CUSUM과 Drift D값의 조건

CUSUM이 잘 작동(변화점을 잘 찾으려면)하려면 변화 이전에는 증가량의 기대값이 음수이고 변화 이후에는 양수여야한다. 

이러한 성질을 만족하면 변화점 이전에는 탐지 통계량이 0 근처에 머물러 임계값을 거의 넘지 않음으로 오탐지를 방지할 수 있다. 변화 발생 후에는 빠르게 해당 통계량이 증가하여 탐지가 가능해진다. 

다만, 아래의 조건으로만은 충분치 않다. 

탐지 성능은 기댓값(mean)뿐만 아니라, 분산(variance) 및 고차(moment) 특성 도 영향을 미치기 때문이다. 

 

따라서 기대값 증가량의 특성을 분석하여 위 조건이 왜 필요한지 알아보자. 

 

CUSUM(8)에서, 시점 t-th Window인 Dte는 아래와 같고 

 

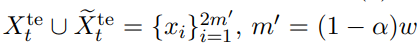
이때 증가량 ηt는 아래와 같다. 

 

이 때 라벨 y는 참조 샘플(reference sample)일 경우 0, 도착 샘플(arrival sample)일 경우 1이다. 

 

적분식으로 이를 변환하면(기대값 정의) 다음과 같다.

 

 위 식에서 arrival sample과 reference samples의 Empirical distribution(경험적 분포)는 아래와 같다. 

이때 δ는 디랙 델타 함수을 의미한다. 

 

식 11에서 볼 수 있듯이 증가량 ηt​ 는 훈련 데이터(즉, θt​) 에 의해 영향을 받으며, 동시에 테스트 데이터(즉, f1(x)-f2(x)인 두 분포의 차) 에 의해서도 결정된다

 

NN-CUSUM이 변화를 탐지할 수 있으려면, 증가량 ηt​ 의 기댓값이 변화 이전에는 0이고, 변화 이후에는 양수가 되어야 한다.

만약, 고정된 함수 g(x)(세타 바를 사용하는 것이 아님) 를 사용한다고 가정하면, 쉽게 다음이 성립함을 보일 수 있다:

즉, g가 아래의 정규성 조건(12)을 만족하면

 

0= E0​[ηt​] < E1​[ηt​]의 관계를 통해 두 E사이에 존재하는 적절한 drift 값인 D를 선택하면

 

CUSUM이 변화 발생 이전에는 기대 증가량이 음수이고, 변화 발생 이후에는 기대 증가량이 양수가 되는 성질을 가지게 할 수 있다. 

 

(12), 즉 정규성 조건을 만족하는 g를 찾기 위해 다양한 NN 모델이 사용가능하다.

 

- NN모델과 정규성 조건을 만족하는 결과함수 g

 

위 정규성 조건(12)을 만족하는 gθ를 찾기 위해 다양한 신경망(neural network) 모델을 사용할 수 있다.
특히, 신경망을 활용한 발산(divergence) 분석, 즉 "Neural Divergence Analysis" 가 효과적이다. 신경망을 이용해 gθ 를 표현하는 방법은 "Neural Distance" 연구 [31] 및 "Neural Estimation of Divergences" 연구 [24] 에서 논의되었다.
이론적으로, 많은 함수 gθ​ 가 정규성 조건(12)을 만족할 수 있지만, 실제 신경망 훈련을 통해 발견되는 gθ가 어떤 것인지는 별개의 문제이다.
또한, 변화 탐지의 효율성은 단순히 gθ​ 의 양의 편향값(positive bias)뿐만 아니라 분산(variance) 도 영향을 미친다.

 

실제 구현에서는, 신경망 매개변수 θ^가 훈련 데이터에 의해 추정되므로 랜덤 변수(random variable) 가 된다.
따라서, 해당 θ^ 의 확률적 특성을 고려하여 분석이 필요하다.

이를 위해 두 단계로 분석을 진행한다

 

1. 고정된 θ^를 가정하고 (훈련 데이터가 주어진 경우),
샘플 증가량 ηt​ 가 모집단 기대값과 어떻게 연결되는지 분석 (섹션 4.2)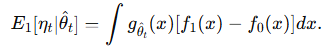 

 

2. E1[ηt|θ^]가 MMD (Maximum Mean Discrepancy) 통계량과 높은 확률로 관련됨을 보이는 과정 

훈련된 신경망 매개변수 θ^t​ 에 대한 확률적 특성 고려 (섹션 4.3)

 

이를 통해, 신경망을 이용한 변화 탐지 방법을 더욱 엄밀하게 설명할 것이다.

4.2 Effect of test samples: Concentration(수렴) over testing data

증가량 ηt의 편차를 해당 값의 가대값으로부터 분석해보자. 

 

해당 값은 훈련데이터 Dtr에 의해서 결정되는 값이다. 

훈련데이터가 주어지는 경우 ηt는독립 합(independent sum)임으로  테스트 샘플 크기 (1−α)w에 의해  편차는 bounded 되며 이는 아래의 Lemma를 통해 보여진다. 

NN-CUSUM이 잘 동작하려면, 변화 전후 데이터가 특정 범위 내에서 집중(Concentration)되어 있어야 신뢰성 있는 탐지가 가능

 

Lemma 4.1 (Concentration on test samples)

가정: NN model의 함수 g(x)가 uniformly bounded 된 함수 집합 G에 속한다고 가정하자. 즉, 어떤 상수 C가 존재하여 아래를 만족한다고 하자. 

sup 는 supremum(상한, 상계 중 가장 작은 값)

그렇다면 임의의 λ1 > 0에 대해 아래의 Probability bound가 성립한다. 

 

 

여기서 i = 0,1 이며 확률 P는 시점 t의 window의 testing split의 확률을 의미한다. 이는 NN-CUSUM의 테스트 샘플이 충분히 많으면, 변화 탐지 통계량이 안정적으로 분포하며 변동성이 적다는 것을 의미한다.

 

4.3 Effect of training: Analysis by Neural tangent kernel (NTK) MMD

MMD 손실(5) 하에서 ηt의 근사값을 고려하며 이를

라고 하자. 이러한 근사는 이후의 분석에 유용하며 neural tangent kernel (NTK) 분석에 유용하다. MMD 손실을 넘어 NTK를 확장하는 것은 현재 활발히 연구되는 분야이다. 

NTK: 복잡하게 멀티레이어로 엮어 있는 뉴럴 네트워크를NTK에 곱해주게 된다면, Linear 모델로 근사하여 모델에 대한 해석을 가능하게 해주는 방식([2018 NIPS] Neural Tangent Kernel - Convergence and Generalization in neural Network)
https://youtu.be/vDQWwOqQ7mo?si=1Q0_J4dSaVo57aKZ 
2 hidden layer와 infinite nodes의 neural network는 linear model로 근사하여 생각할 수 있고, 그 덕분에 문제를 convex 하게 만들어 해가 반드시 존재한다는 것을 보여준다. 

 

 

기본적으로 변화가 발생하지 않는 경우 항상

는 성립한다. 

 

그러나 변화 이후

임을 보이려면, 훈련 과정에서 이를 보장해야한다. MMD 손실(5)을 사용하여 훈련하면, 높은 확률로 이 조건이 만족됨을 보조 정리 4.2 (Lemma 4.2) 에서 보인다. 

 

학습은 윈도우 (t−w,t] 에 대해 한 번의 확률적 경사 하강법(SGD) 스텝을 수행하는 방식으로 진행 되며, 총 2m개의 샘플을 사용하여 작은 학습률 γ>0 아래에서 이루어진다. 따라서 g는 아래와 같이 정의된다. 

NTK 근사에 따르면,  data domain X에 대해 아래와 같다. 

 

이때,  훈련 샘플의 empirical distributions은 아래와 같고, 

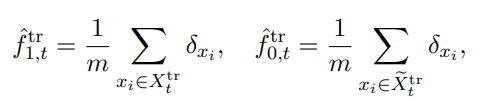
초기 신경망에 대한 NTK은 

이다.  이때, 상수 C는 신경망 함수의 유계성과 도함수의 유계성에 따라 결정된다([7]의 Proposition 2.1 및 Appendix A.2 참고)

위 근사(14)를 사용하면, 증가량 ηt 는 다음과 같이 근사될 수 있다: 

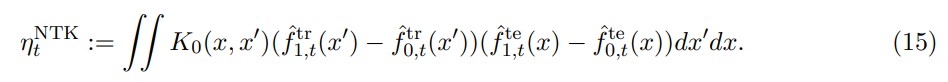
학습에서 기대 증가량 조건에 따라 (14)로 부터 아래를 알 수 있다. 

한편, 전체 기댓값 E1[η NTK]는 커널 K0에 대한 f1과 f0 사이의 제곱된 모집단 커널 MMD와 동일함에 유의하라[8]

 

정의에 따라, MMD²(f0, f0) = 0이다. 본 논문에서는 f1 ≠ f0일 때 MMD²(f1, f0) > 0이라고 가정하는데, 이는 NTK 커널 K0가 충분히 판별력이 있어 변화 이후 양의 MMD²(f1, f0)를 생성함을 의미한다. 이를 종합하면, 양의 Drift 기대값을 얻는다. 

 

따라서, γ가 모집단 제곱 MMD에 대해 충분히 작을 때 E1[ηt] > 0이다.

 

이를 통해, 신경망을 이용한 CUSUM 탐지가 효과적으로 작동하기 위해서는 γ 가 충분히 작고, MMD 값이 양수여야 함 을 알 수 있다.

추가적으로, 다음 Lemma 2는 충분히 큰 유한한 훈련 샘플 크기 αw에서 E1[η NTK t | Dtr t]의 양의 값을 보장한다.

 

Lemma 4.2 (Guarantee under MMD loss).

임의의 x,x′∈X 에 대해 NTK 커널 K0(x,x′)가 유계(bounded)하여

라고 하자.

임의의 λ2​>0에 관하여

가 성립한다.

 

(19)와 (16)식을 결합하면 t번째 윈도우에서 훈련 데이터 D tr의 랜덤성에 대한 확률 w.p.으로 

보조정리 4.1에서의 테스트 샘플의 수렴에 관한 내용과 결합하면, 아래의 확률로 

 (21)이 성립한다. 

 

따라서, 신호(signal) MMD2(f1,f0)가 충분히 크고, w가 충분히 크며, γ가 작게 조정될 경우, 증가량이 높은 확률로 양수가 됨을 보장할 수 있다. 또한, 드리프트 항 D를 충분히 작게 선택하면 NN-CUSUM 증가량 ηt−D가 여전히 높은 확률로 양수임을 보장할 수 있다. 즉,  NN-CUSUM 탐지가 효과적으로 작동함을 보장 할 수 있다.

 

4.4 EDD and ARL performance

이제 검출 속성을 분석해 보자. 고전적인 CUSUM 분석에서는 증가량이 로그 가능도 비( e.g., exact or with plug-in parameter estimators)를 기반으로 하지만, 여기서는 증가량이 직접적으로 가능도 비와 관련되지 않음을 유의해야 한다. 따라서 고전적인 결과(예: [22]의 섹션 6)를 그대로 적용할 수 없다. 그러나 우리는 여전히 Wald’s identity와 유사한 분석을 활용하여 NN-CUSUM 절차가 변화를 얼마나 빠르게 감지할 수 있는지를 분석할 수 있다.

 

순차적 변화점 검출에서 일반적으로 사용되는 두 가지 성능 지표는 다음과 같다.
(i) 평균 실행 길이(ARL, Average Run Length): 변화가 발생하지 않은 경우 정지 시간의 기댓값을 나타냄.
(ii) 기댓값 탐지 지연(EDD, Expected Detection Delay):

 

아래에서는 Worst case에서의 탐지 지연이 아니라, 분석을 단순화하기 위해 변화가 처음부터 즉시 발생하는 경우의 EDD를 고려한다. 이를 통해 알고리즘 설계 및 탐지 성능을 이해할 수 다. 이론적인 ARL 분석은 향후 연구로 남겨두며, 실무에서 ARL을 제어하기 위한 임계값 선택은 섹션 5.2에서 설명한다.

 

4.4.1 i.i.d. increments

우선 단순화된 설정을 고려하자. 

훈련 과정에서 현재 시점에서 다음 시점까지 훈련 윈도우와 테스트 윈도우가 겹치지 않는 경우를 가정하는데, 이는 stride s=w이다. 

또한 매 시점 t에서 파라미터 θt가 새로운 초기값으로 학습된다면 파라미터는 t에 따라 독립적이지 않다.

이러한 설정에서 우리는 ηt가 iid라고 가정할 수 있고, 따라서 EDD에 대한 추정이 가능하다. 

 

먼저 Wald's identitiy를 보자. 

 

Lemma 4.3 (Wald’s identity)

Xn, n = 1, 2, . . . 을 실수 값을 가지는 무한한 확률 변수 연속이라고 하자. 또한 N을 non
nonnegative integer-valued random variable이라 하자. 

(i) Xn are all integrable (finite-mean)

(ii) E[XnI{N ≥ n}] = E[Xn]P(N ≥ n) for all n, and

(iii) the infinite series satisfies

즉, 수렴한다고 하자. 

그러면 아래의 random sum이 적분 가능하고

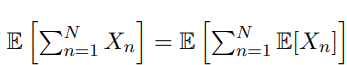
추가로 

(iv)  모든 n에 대해 아래가 성립한다. 

(v) E[N]<∞ 이면,

 

CUSUM의 재귀 관계는 단순 random walk과정이 아니기에 단순화하기 위해 

라 하자. 

 

EDD의 상한을 유도하기 위해 표준편차를 이용하여 아래와 같이 CUSUM의 탐지 통계량(8)을 유도할 수 있다. 

이는 sequential likelihood ratio test, SPRT을 위해 유도된Stein의 보조정리(Stein’s lemma)와 유사하다(예: [22]의 명제 2.19 참고). 이제, 이 결과를 이용하여 f0와 f1모두에서 성립할 수 있는 추가적인 결과를 도출할 수 있다.

 

Lemma 4.4 (Finite expected stopping time for general CUSUM with i.i.d. increments)

X1​, X2​,…가 i.i.d.라고 하자. 그러면 CUSUM 재귀 관계를 다음과 같이 정의한다.

또한, 정지 시간을 

로 정의한다. 

 

만약 어떤 작은 δ∈(0,1)에 대하여 

가 성립하면, 

 

일반적으로 CUSUM의 기댓값 탐지 지연(EDD)을 엄밀밀하게 특성화하려면, 비선형 갱신 이론(non-linear renewal theory)을 사용하여 b→∞ 극한을 분석, 가능도 비(likelihood ratio) 기법을 일반화하는 과정이 필요하다 ([22]의 Section II.6 참고).

그러나, 아래에서는 보다 단순한 접근법을 사용하여 NN-CUSUM의 EDD에 대한 상한을 유도한다.

 

 

Theorem 4.5 (EDD bound for NN-CUSUM, i.i.d. increments)

아래의 가정을 하자. 

그럼 NN-CUSUM의 기댓값 탐지 지연(EDD)은 다음과 같은 상한을 갖는다.

 

위 식에서 O(1) 항은 기댓값 오버슈트(expected overshoot)

 

에 기인하며, 일반적으로 증가량의 기댓값 크기와 같은 차원이다. 이에 대한 자세한 분석은 [22, 27] 등을 참고할 수 있다.

 

 

EDD의 상한식 (27, Proof section에 있음)

 

과 likelihood-ratio based CUSUM 의 상한

을 비교해보자. 이때 KL은 Kullback -Leibler Divergence이다. 

NN-CUSUM의 경우 신경망 훈련 손실 함수의 선택 및 NTK(Neural Tangent Kernel)의 특성으로 인해, likelihood-ratio based CUSUM의 잘 알려진 좋은 상한보다 더 느슨한 상한을 갖는다. 

 

이론적으로 만일 logistic loss를 loss로 선택하면 위 KL 식을 이용한 상한을 달성할 수 있다. 그러나 실무적으로 logistic loss는 non-linearity한 특성이 강하기 때문에 NTK 분석을 일반화하는 것이 어렵고, 잘 아려진 바와 같이 신경망이 로그 가능도 함수에 수렴하도록 훈련하는 것이 어렵다.

 

Remark 4.2 (ARL approximation for NN-CUSUM, i.i.d. increments).

 

변화가 없는 경우, 즉 f0 하에서 ARL(평균 런 길이, Average Run Length)을 고려하자. τ (b)는 임계값 b에 대하여 

점근적으로(large bbb) 지수 분포를 따른다는 것을 보일 수 있다.

 

• 포아송 근사(Poisson approximation): [14]의 보조정리 D.1 및 [30]의 정리 1에서 사용됨.
• 확률 측도 변경 기법(Change-of-measure technique): [26]의 보조정리 2에서 ηt\eta_tηt​가 i.i.d.일 때 활용됨.

직관적으로, b가 클 때 다음 확률이

의 형태를 가질 것으로 예상된다. 특히, ttt 또한 클 때 이 근사는 더욱 정확하다.

이러한 점근적 지수 분포 성질은 ARL 시뮬레이션을 단순화하는 데 매우 유용하다. 예를 들어, 임계값 b의 조정을 위한 시뮬레이션(Section 5.2 참고)에서 활용될 수 있다.

또한, 비점근적(non-asymptotic) 상황에서도 높은 정확도를 유지한다는 점이 섹션 5.1의 수치 실험(numerical examples)을 통해 확인되었다

4.4.2 m-dependent stationary process

대부분의 시나리오 상 ηt는 dependent할 가능 성이 있다. 이러한 의존성은 stride 𝑠가 윈도우 길이 𝑤보다 짧을 때 발생할 수 있다.
즉, 시점  𝑡에서 𝑡+1로 이동할 때 훈련 및 테스트 데이터가 크게 겹치는 경우가 있다.
그러나, 알고리즘 설계 방식 덕분에 𝑤/𝑠 스텝 후에는 훈련 및 테스트 데이터가 완전히 새로운(non-overlapping) 데이터로 대체된다.
즉, 시점 𝑡+𝑤/𝑠에서는 시점 t와 겹치지 않는 데이터가 사용된다.

 

또한, 만약 신경망이 무작위 초기화(random initialization)된 상태에서
현재 훈련 데이터만을 사용하여 학습된다면, 𝜂𝑡는 𝑚-의존적(m-dependent) (여기서 𝑚=𝑤/𝑠) 이라고 가정할 수 있다.
즉, 𝑠≥𝑤/𝑠 일 때 𝜂𝑡 는 s 시점 전 과거의 𝜂𝑡−𝑠 ​와 독립적이다.

그럼으로 의존성을 고려한 Wald’s Lemma 확장이 필요하다.  이전 섹션과 유사한 방식으로 분석하려면, 의존적이지만 유한한 메모리를 가진 시퀀스(dependent but finite-memory sequences)를 다룰 필요가 있다.

이와 관련된 연구 결과는 이미 [18]에서 개발되었다. 아래에서는 [27]의 증명 전략과 유사한 방법을 사용하여
우리의 시나리오에 적합한 Wald’s 정리 버전을 유도한다.

 

Lemma 4.6 (Generalized Wald’s identity for m-dependent sequence).

Consider: 

 

• stationary sequence of random variable Xn, n=1,2,.... 을 가정
• Xn​은 유한하고 양의 평균을 가진다 E[Xn]>0
• Xn은 m-의존적(m-dependent), ie Xn는 Fn-s for all s>m 에 독립이다( m 간격 이후에는 독립이라는 것을 의미 그보다 먼 과거의 값들과는 독립적)
• Stopping time N: 일정한 임계값 bb를 초과하는 최소한의 시간. 즉, 누적 합이 b를 초과하는 최초의 시점

If E[N] < ∞ : 

 

O(1) 항은 정지 시간 N에서 임계값b를 초과하는 오버슈트(overshoot) 기댓값에서 유래되는 보정항이고, m은 m 종속성에 관한 항이다

 

Theorem 4.7 (EDD upper bound under m-dependent stationary process)

Consider: 

주어진 확률 과정 ηt가 정상(stationary)이고, 기대 탐지 지연(expectation of detection delay) E1[τ]가 유한하다고 가정한다.

 

결과

 

Theorem 4.7에 관한 증명은 Therem 4.5에 관한 증명과 유사하며 Lemma 4.6을 사용한다. 증명에 있어서 ηt가 Stationary하다는 가정이 필요한데, 이는 데이터가 iid이고, m-dependency는 휸련 및 테스트 스택 overlapping에 의해 생성됨으로 Stationay함을 가정해도 무방하다(즉 m가지는 종속성을 가질 수 있음).

또한 E1[τ]가 유한함을 가정하는데 이는 Lemma 4.4의 논증을 m-dependent sequence에 관해 일반화해야함으로 기술적으로 복잡하여 생략한다. 그러나 실험적으로 탐지가 함리적인 시간 내에 멈춤을 확인 가능했다. 

식 (25)와 (27)을 비교할 때, 우리는 식 (25)에 ηt의 기억 효과(memory effect)로 인해 윈도우 w에 관한 추가적인 항이 도입됨을 알 수 있다.

 

Remark 4.3 (Effect of window length w)

윈도우 길이 w 선택에는 **트레이드오프(trade-off)**가 존재한다. 

큰 w의 경우 신호 ηt ​가 목표하는 MMD2(f1,f0)에 가까워지므로, 탐지 정확도가 높아진다.

이는 식 21에서 확인 가능하듯이 테스트 데이터의 랜덤성으로 인해 발생하는

훈련데이터의 랜덤성으로 발생하는

를 작게 조절하기 위해(분모에 위치) 충분한 w의 크기가 필요하다. 

 

다만, (25)에서 EDD의 상한을 선형적으로 증가시키는 요인이 되기에 실험적으로 적절한 w가 존재한다는 것이 관찰하였고, 이를 Section 5.4에서 분석한다. 

 

향후 연구에서는, i.i.d. 증가분에서 m-dependent인 경우로 ARL(Average Run Length) 근사를 확장하는 방향으로 주석 4.2를 확장할 수 있으며, [14]와 유사한 기법 및 종속성을 허용하는 일반화된 포아송 근사(generalized Poisson approximation) [3]을 사용할 수 있을 것이다. 

 

5 Experiments

NN-CUSUM의 성능을 검토하기 위해, 우리는 시뮬레이션된 데이터셋과 실제 데이터셋에서 제안된 방법을 다양한 기준선(기존 NN 기반 방법 및 고전적 방법)과 비교한다. 비교에 앞서, 우리는 f0f 하에서 τ의 지수 분포를 검증하고, 오경보(변화가 없을 때 변화를 감지하는 경우)를 제어하기 위해 임계값을 보정하는 방법과 증가량의 특성과 최적 w를 조사하는 수치적 연구를 포함하여 알고리즘의 몇 가지 세부 사항을 소개한다.

 

5.1 Verifying exponential distribution of τ under f0

f0 하에서 τ 의 점근적 분포가 지수 분포임을 확인해보자. 

Setup.

이 예제에서 NN-CUSUM의 신경망 아키텍처는 너비 64의 Fully connected layer 하나로 구성되며, 활성 함수로 ReLU(Rectified Linear Unit)를 사용한다. 마지막 층은 활성 함수가 없는 1차원 FC 층이다. 훈련 배치 크기는 100이다. 슬라이딩 윈도우의 스트라이드는 10이다. 우리는 로지스틱 손실 함수 하에서 Adam [11] 옵티마이저를 사용하여 학습하며, 학습률은 스케줄링 없이 10^-3로 설정한다. 윈도우 크기는 𝑤=200 분할 비율은 𝛼=0.5로 설정한다.

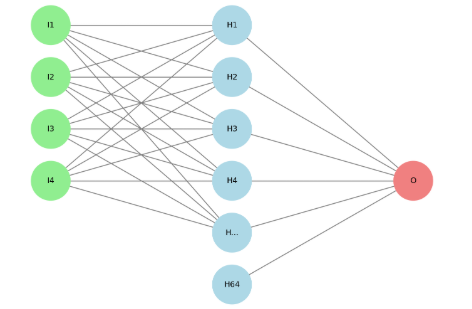
Connected NN-CUSUM layer 모델 그림

본 실험에서는 총 길이 40,000인 500개의 시퀀스를 생성하며, 각 시퀀스는 R 100 공간에서 독립적으로 동일하게 분포된(i.i.d.) 표준 정규 난수로 구성된다. 이 예제에서는 𝜏의 꼬리 확률을 연구하므로 변화점이 존재하지 않는다. 식 (9)에서 임계값 𝑏=1로 설정한다.

Results

Fig 3에서 실선은 몬테카를로 실험을 통해 얻은 𝜏 의 경험적 꼬리 확률을 나타낸다. 이를 비선형 회귀를 통해 곡선 P{τ>t}=e ^−λt
에 맞추었으며, 그 결과  𝜆=6×10 ^−4 를 얻었다. 그림 에서 볼 수 있듯이,  지수분포와 경험적 꼬리 확률 간의 일치는 매우 좋은 결과를 보인다.

 

5.2 Calibration of threshold b

E0​[τ] 의 기댓값을 추정하기 위해 τ 를 직접 시뮬레이션하는 것은 계산적으로 매우 비용이 많이 든다. 임계값 b가 고정될 때, 이를 추정하려면 다수의 반복 실험이 필요하며, 특히 변화가 없을 때 큰 ARL(Average Run Length, 평균 런 길이)을 얻기 위해 b를 조정하는 것이 일반적이므로 각 반복에 많은 시간이 소요된다. 따라서 우리는 [29]에서 사용된 유사한 기법을 적용하여 ARL 추정을 위한 시뮬레이션 속도를 높인다.

Remark 4.2에서 언급했듯이, 데이터가 f0에 따라 i.i.d.하게 분포할 때(즉, 변화점 이전), 정지 시간 τ 는 점근적으로 어떤 λ>0\에 대해 지수 분포를 따른다. 따라서 지수분포로 근사할 수 있다. 

 

이를 이용하여 λ의 추정값을 평가할 수 있으며 ARL은 지수분포의 평균은 그 lamda의 역수임으로 아래가 성립한다. 

이 방법을 활용하면, τ를 직접 시뮬레이션하는 대신(변화가 없을 때 큰 ARL을 얻기 위해 긴 실행이 필요하므로 계산 비용이 큼) 고정된 길이 T 의 시퀀스를 시뮬레이션하고, 해당 시퀀스가 임계값 b 를 초과할 확률을 추정하는 방식으로 변환할 수 있다.

 

Fig 4는 GMM(Gaussian Mixture Model)에서 생성된 400개의 변화 이전(pre-change) 시퀀스를 사용한 예제에서 임계값 b에 따른 ARL을 보여준다. 또한, 로그 스케일에서 ARL이 임계값 b에 대해 대략적으로 비례 관계를 가지며, 이는 CUSUM 절차의 일반적인 특성임을 확인하였다 [28].

5.3 Properties of increment ηt

increment, 증가량 ηt가 NN에 의해서 change point이전에는 거의 0에 가깝고 이후는 유의미한 양수의 값인지 실험적으로 검증한다. 

Setup.

 

NN-CUSUM의 신경망 설정은 섹션 5.1과 유사하지만, 숨겨진 층의 너비를 512로 확장하고, 배치 크기를 10으로 조정한다. 신경망은 가우시안 희소 평균 이동(Gaussian sparse mean shift) 예제에서 훈련되며, 이는 표 2의 첫 번째 예제에 해당한다. 여기서 평균 벡터는 다음과 같이 설정된다.

여기서 δ = 0.8이다. 분할 비율 α=0.5, 윈도우 크기는 {20,60,100,200}중에서 변화시킨다. 데이터는 충분히 긴 길이인 2 * 10^5로 생성되며, 이를 통해 ηt의 샘플 평균이 안정적으로 계산되게 하였다. Mean shift는 중간 지점인 1 * 10^5 시점에서 발생한다. 

 

로그 가능도 비율(Log-likelihood ratio, LLR) 분석을 위해 훈련 시 윈도우 크기 w=300, 분할 비율 α=1/3으로 설정한다. 변화점은 5000에서 발생한다. 실험에서 사용한 time horizon은 {5000,5080,5160} 중 하나이다. 

 

각 time horizon마다 1000개의 테스트 포인트를 생성하며, 이 중 절반은 f0 에서, 나머지 절반은 f1​ 에서 생성된다. 그런 다음, 테스트 데이터에서 진짜(true)와 학습된(learned) 로그 가능도 비율을 계산한다.

 

Results.

 

표 1은 변화 이전(pre-change)과 변화 이후(post-change)에서의 ηt의 시간적 평균(temporal mean)을 보여준다. 윈도우 크기 w=20 일 때부터 변화 이후(post-change)의 기대 ηt가 양수가 되며, 윈도우 크기가 증가할수록 ηt의 크기가 더 커진다.

 

Fig 5 는 다양한 w 에 대해 변화 이전과 이후의 ηt 경험적 분포를 시각적으로 보여준다. 훈련 및 테스트 윈도우 크기가 증가할수록 ηt 의 평균 이동(mean shift)이 더 뚜렷해지며, 이는 더 빠른 변화 탐지를 가능하게 함을 시사한다(표 1과 일관된 결과).

이번 실험에서, NN-CUSUM 절차는 윈도우 크기 w=20 에서도 양의 기대 ηt를 얻었으며, 이는 섹션 4.1 에 따르면 변화점을 감지할 수 있음을 의미한다. 그러나 윈도우 크기 w 를 선택할 때 트레이드오프가 존재함으로, 더 큰 w는 ηt 의 이동 크기를 증가시키지만 탐지 지연을 초래할 수 있다.

 

5.4 Optimal window size

우리는 Remark 4.3 에서 논의된 대로 윈도우 크기 www 선택의 트레이드오프를 실험적으로 조사한다.

 

Setup. 

신경망 구조, 배치 크기, 그리고 스트라이드는 섹션 5.3과 동일하다.
분할 비율 α 는 {0.1,0.2,0.4,0.8}에서 선택되며, 윈도우 크기 w는 {200,400,…,1200} 범위에서 변화한다.

이번 실험에서 사용된 예제는 GMM(Gaussian Mixture Model)에서 구성 요소 이동(Component Shift) 이 포함된 표 2의 네 번째 예제이다. 보다 구체적으로, 분포는 다음과 같이 정의된다.

 

변화 이전:

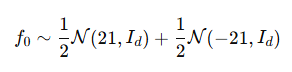
변화 이후:

 

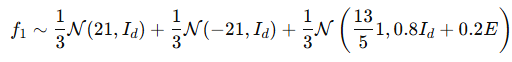
총 400개의 시퀀스를 생성하며, 각 시퀀스 길이는 10,000, 변화점은 중간인 5,000 에 위치한다.

 

 

Results.

 

Fig 6a 에서 점선 곡선은 모든 α 에 대해 최소 EDD(Expected Detection Delay, 기대 탐지 지연) 를 나타낸다.
최적의 EDD는 모든 w 와 α조합에서 가장 낮은 EDD를 형성하는 경계선(lower envelope)을 따른다.
최적의 w 는 ARL이 증가함에 따라 커지는 경향을 보이며, 이는 해당 경계선과 일치하는 곡선이 점차 오른쪽으로 이동하는 것으로 확인할 수 있다.

Fig 6b 는 Remark 4.3 을 정당화하며, 임계값 b 가 증가할수록 최적의 w가 단조 증가함 을 보여준다.
Fig 4 는 ARL과 임계값 b간의 단조 관계를 나타내며, Fig  6b와 Fig 4를 종합하면, ARL 증가에 따라 최적의 w가 커지는 경향이 Fig 6a와 일관됨을 확인할 수 있다.

 

5.5 Comparison on simulated data

본 장에서는  제안된 NN-CUSUM 과 기존 방법 및 관련 기법을 포괄적으로 비교한다. 표 2 에 시뮬레이션에 사용된 10개의 예제의 분포에 관한 설명이 있으며 예제들은 평균(mean) 및 공분산(covariance)의 변화가 작거나(혹은 거의 없음) 희소(sparse)한 상황을 고려하여 탐지가 어려운 환경으로 설계되었다. 

 

Setup

• 시뮬레이션 비교에서 NN-CUSUM의 신경망 아키텍처는 섹션 5.1 의 예제와 동일
• 윈도우 크기: w=20, 분할 비율: α=0.5
• 시퀀스 총 길이: 5500, 변화점: k=500에 위치함(즉, 변화 이전 구간은 500)
• ARL 보정: 섹션 5.2 의 ARL = 5000 을 적용하여, 제1종 오류(Type-I Error) 를 10% 이하로 조절함.
• 400개의 시퀀스를 생성
• 모든 방법은 길이 15,000인 변화 이전 데이터(참조 데이터) 400개 를 공유하며, 이를 통해 사전 변화(pre-change) 과정의 통계적 특성을 학습함.
• NN 기반 방법(NN-CUSUM, ONNC, ONNR) 은 신경망을 안정화하기 위해 변화 이전 데이터(길이 5000)에서 먼저 학습(burn-in 과정)한 후 탐지를 시작
• 모든 시뮬레이션 실험에서 데이터 차원은 100 으로 설정됨.

Baselines for comparisons.

 

비교 대상 베이스라인(Baselines)은 아래의 7가지 기존 방법이다. 

1. Online Neural Network Classification (ONNC)
2. Online Neural Network Regression (ONNR)
3. Window-limited Generalized Likelihood Ratio (WL-GLR)
4. Window-limited CUSUM (WL-CUSUM)
5. Multivariate Exponentially Weighted Moving Average (MEWMA)
6. Hotelling-CUSUM (H-CUSUM)
7. Exact CUSUM (이 방법은 변화 전후의 분포를 완전히 알고 있으므로, 모든 방법의 탐지 지연(EDD)에 대한 하한을 제공함)

베이스라인 구현 세부 사항은 부록 B.1 참고

 

Results

 

 

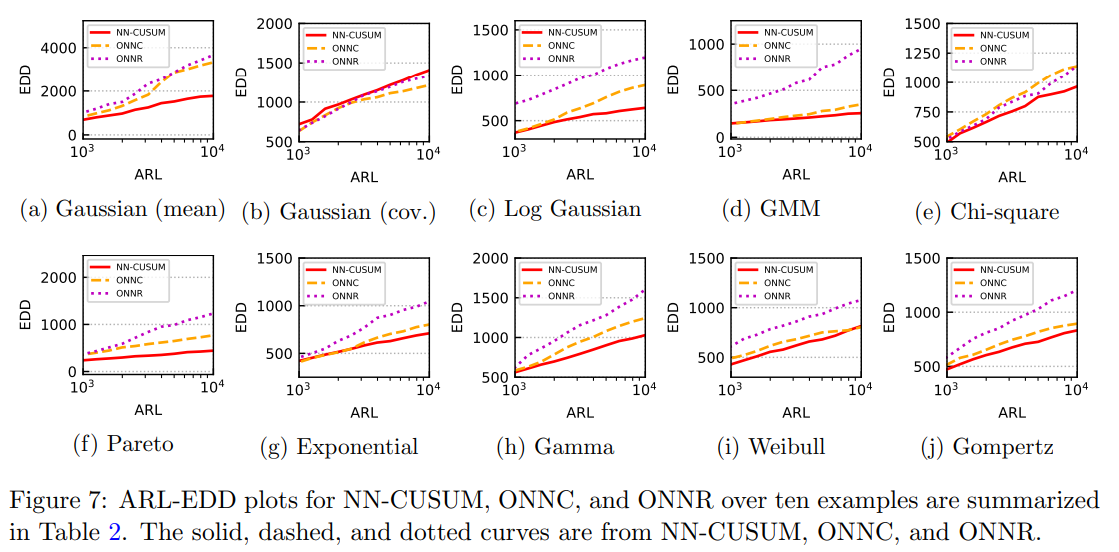
1. NN 기반 방법과의 비교

Fig7 에서 NN-CUSUM은 모든 실험에서 ONNC 및 ONNR보다 빠르게 탐지하나 단, Gaussian covariance shift에서는 예외적 이 경우 NN-CUSUM의 성능이 ONNC 및 ONNR과 유사하였다. 

NN-CUSUM이 다른 NN 기반 방법보다 우수한 이유로 실험에서 변화점을 탐지하는 것이 어렵도록 설계되었기 때문이라고 저자들은 주장한다. 즉, 작은 변화(small magnitude), 희소성(sparsity), 기댓값 고정(fixed expectation) 등의 설정을 사용하여 데이터를 생성하였고, ONNC와 ONNR은 일반적인 분포 변화(distributional shift) 탐지 가능 하지만, Shewhart chart 유형 ([28] 참고)에 대한 대한 민감도가 낮아 NN-CUSUM보다 탐지가 느린것으로 보인다. 

 

2. 기존 방법(classic methods)과의 비교

 

표 3 은 ARL = 5000 에 대해 모든 방법의 EDD(기대 탐지 지연) 을 요약한 결과이다. 그 결과 NN-CUSUM이 대부분의 기존 방법보다 탐지 지연이 짧음(빠르게 탐지). 기존 방법의 탐지 성능은 그들이 가정하는 분포 특성이 유지되는지 여부에 따라 달라짐

가정이 충족될 경우 탐지가 가능하지만, 변화의 크기가 작거나 노이즈가 심하면 탐지 성능 저하되었다. 

Gaussian sparse mean shift 및 Gaussian sparse covariance shift 실험에서 확인되었듯이 

모든 방법이 어느 정도 변화 탐지가 가능하지만, 희소성(sparsity)과 작은 변화량(small magnitude) 때문에 탐지 속도가 느림

또한. 기존 방법(classic methods)은 1차(moment) 및 2차(moment) 통계량 을 사용하여 분포 변화를 탐지 즉, 전통적인 방법들은 그들의 가정이 트린 경우에도 작동할 수 있지만 변화점 탐지가 기대값(mean) 또는 분산(variance)의 명확한 변화가 있어야한다. 

예로 WL-GLR 및 WL-CUSUM 은 평균 이동(mean shift)에 민감하고 H-CUSUM 은 분산 증가(variance increase)에 민감하지만 실험에서는 평균과 분산의 변화가 미미하거나 거의 없다. 그럼으로 기존 방법론들이 실패할 가능성이 높다. 

 

5.6 Real data experiments

우리는 NN-CUSUM 과 기존 방법들의 성능을 평가하기 위해 두 가지 실제 데이터셋 을 사용하여 변화점 탐지(change-point detection) 실험을 수행한다.

• Higgs boson dataset
• MiniBooNE dataset

- Dataset

Higgs Boson 데이터셋: 

고에너지 입자 충돌 실험에서 희귀한 입자(예: 힉스 보손)를 발견하는 것은 중요한 연구 주제로 머신러닝 기법은 이러한 희귀 입자를 탐지하는 데 자주 사용되고는 한다. 
이를 위해 신호(signal) 대 배경(background) 분류 문제 를 해결해야 한다([4). 본 실험에서는 Higgs boson 데이터셋 을 활용하여 변화점 탐지 문제 로 변환함.

• 데이터셋 구성:
  • 힉스 보손 신호(signal)
  • 힉스 보손을 생성하지 않는 배경 신호(background)
  • 총 1천만 개의 샘플 (몬테카를로 시뮬레이션으로 생성)
  • 28개의 수치형 특징(features) 포함
    • 21개: 입자 검출기로 측정된 운동학적 속성(kinematic properties)
    • 7개: 위의 21개 특징을 이용해 물리학자들이 도출한 고차원(high-level) 특징
  • 본 실험에서는 28개 특징을 모두 사용 함.

MiniBooNE 데이터셋: 

 중성미자(neutrino)는 질량이 매우 작고 전기적 전하가 없어 탐지가 어렵다(2).  MiniBooNE 실험 은 중성미자 진동(neutrino oscillations)을 탐색하기 위해 설계되었고, MiniBooNE 데이터셋 은 이 실험에서 얻은 데이터를 포함함.Higgs boson 데이터셋과 유사하게, 변화점 탐지 문제로 변환하여 실험을 수행 함.

• 데이터셋 구성:
  • 약 13만 개 샘플 포함
  • 배경 신호(background signals) 또는 전자 중성미자(electron neutrinos) 샘플로 구성됨.
  • 50개의 수치형 특징(features) 포함
  • 본 실험에서는 50개 특징을 모두 사용 함.

실험에서 각 데이터셋의 비배경 신호(non-background signal) 를 타겟 신호(target signal) 로 정의하였으며 두 데이터셋 모두 University of California Irvine (UCI) 머신러닝 저장소 에서 다운로드 가능 ([1] 참고)하다. 

 

-Baselines 

• 시뮬레이션 실험과 동일한 베이스라인 을 사용:
  1. WL-GLR (Window-limited Generalized Likelihood Ratio)
  2. WL-CUSUM (Window-limited CUSUM)
  3. H-CUSUM (Hotelling-CUSUM)
  4. MEWMA (Multivariate Exponentially Weighted Moving Average)
  5. ONNC (Online Neural Network Classification)
  6. ONNR (Online Neural Network Regression)
• Exact CUSUM 제외 → 실제 데이터의 진짜 분포를 알 수 없기 때문 에 제외됨.

- Setup

각 데이터셋에 대해 기준(reference) 시퀀스와 온라인(online) 시퀀스를 구성하며, 온라인 시퀀스에만 변화점(change point)이 존재한다.

우선 Higgs boson 데이터셋을 사용하여 기준 시퀀스와 온라인 시퀀스를 각각 500개 생성한다.
하나의 reference 시퀀스는 배경 신호(background signal)에서 추출한 3500개의 데이터 샘플을 포함하며, 하나의 온라인 시퀀스는 목표 신호(target signal)에서 추출한 500개의 데이터 샘플과 배경 신호에서 추출한 3000개의 데이터 샘플을 포함하므로, 온라인 시퀀스에서 변화점은 시간 인덱스 500에서 발생한다.

MiniBooNE 데이터셋을 사용하여 유사한 방식으로 기준 시퀀스와 온라인 시퀀스를 각각 100개 생성한다. 하나의 기준 시퀀스는 배경 신호에서 추출한 1200개의 데이터 샘플을 포함하며, 하나의 온라인 시퀀스는 배경 신호에서 추출한 500개의 데이터 샘플과 목표 신호에서 추출한 700개의 데이터 샘플을 포함하므로, 온라인 시퀀스에서 변화점은 시간 인덱스 500에서 발생한다.

우리는 NN-CUSUM, ONNC, ONNR에 동일한 신경망 구조를 사용하고, 신경망은 하나의 1024 너비의 hidden layer를 가지는 fc이며 활성화 함수로 ReLU를 사용한다.

윈도우 크기는 모두 100으로 설정된다. NN-CUSUM, ONNC, ONNR의 학습 배치 크기(batch size)와 슬라이딩 윈도우(stride) 크기는 10으로 설정된다. 또한, NN-CUSUM, ONNC, ONNR의 학습을 위해 길이 500의 초기 시퀀스(burn-in sequence)를 설정된다. NN-CUSUM, ONNC, ONNR의 신경망 학습에는 Adam 옵티마이저를 사용하며, 학습률은 스케줄링 없이 10^−3으로 설정된다.

제1종 오류(Type-I error).

정확한 데이터에서 거짓 경보(false alarm) 제어를 위해 ARL(평균 런 길이, Average Run Length)은 적절한 지표가 아닐 수 있다. 연구에서는 변화가 특정 시간 내에 빠르게 감지되는 능력에 관심이 있기 때문에 ARL의 대안으로 제1종 오류를 사용한다.

제1종 오류는

로 정의되며, 이는 f0 하에서 변화점 k이전에 탐지 절차가 경보를 발생시킬 확률을 나타낸다(오경보).

임의로 고정된 b에 대해, 탐지 절차가 k+1이전에 중지되는 것은 사건

과 동일하다.

즉, 제1종 오류는 empirical frequency of 사건을 통해 근사 가능 하다.

 

- Results

 

그림 8a는 Higgs boson 데이터셋에서 NN-CUSUM과 기존 방법들의 평균 탐지 지연(EDD)과 다양한 제1종 오류(Type-I error) 간의 관계를 보여준다. 제1종 오류 값은 {0.02, 0.04, …, 0.18, 0.20}에서 선택되고. 그 결과 NN-CUSUM이 제1종 오류가 {0.02, …, 0.12} 범위에 있을 때 모든 다른 기존 방법들보다 일관되게 우수한 성능을 보인다는 것을 확인했다.

또한, 탐지 절차가 변화점을 감지하지 못하는 빈도를 평가하기 위해 탐지 실패율(detection failure rate)을 계산하였다. 이때 탐지 실패율은 위에서 정의한 사건이 발생하는 빈도로 정의된다.

표 4는 Higgs boson 데이터셋에서 제1종 오류 {0.02, 0.10, 0.20}에 대한 NN-CUSUM과 기존 방법들의 탐지 실패율을 보여준다. NN-CUSUM, ONNC, ONNR은 모든 제1종 오류 값에서 0의 탐지 실패율을 달성했다.

그림 8b는 제1종 오류 {0.02, 0.04, …, 0.18, 0.20}에 따른 EDD를 나타낸다. NN-CUSUM은 제1종 오류 {0.02, 0.04, 0.06}에서 기존 방법들보다 우수한 성능을 보이지만, 높은 제1종 오류에서는 WL-CUSUM과 MEWMA가 NN-CUSUM보다 더 나은 성능을 보였다. 그러나 표 4에서 확인할 수 있듯이, NN-CUSUM은 모든 기존 방법들 중에서 가장 낮은 탐지 실패율을 일관되게 유지하였다. 

6 Conclusion

본 논문은 Online change point detection을 위한 신경망 기반의 방법론을 제안한다. 본 논문에서 학습된 이진분류 신경망 모델을 테스트 배치에 적용하여 얻은 증가량 ηt 을 사용하여 CUSUM 순환(recursion)을 수행한다. 

이는 로지스틱 손실(logistic loss)의 훈련이 (확률적 관점에서) 두 샘플 간의 로그 가능도 비율(log-likelihood ratio)로 수렴한다는 점에서 비롯되며, 따라서 순차적으로 학습된 신경망을 사용하여 테스트 샘플에 대해 CUSUM 통계를 구성하는 것으로 이어진다.

 

이후 광범위한 수치 실험을 통해 우리는 제안된 절차가 기존의 고전적인 통계 방법 및 다른 신경망 기반 방법들과 비교하여 경쟁력 있는 성능을 보이며, 시뮬레이션 데이터와 실제 데이터 실험 모두에서 우수한 성능을 발휘함을 입증하였다.
추가로 이를 더욱 일반화하여 MMD 손실과 같은 다른 학습 손실에도 적용하며, 이를 통해 신경 탄젠트 커널(NTK, Neural Tangent Kernel) 분석이 가능하게 하였다. 제안된 NN-CUSUM 절차의 이론적 성능을 설명할 수 있도록 훈련 및 테스트 데이터를 분할하여 사용하는 새로운 온라인 절차를 개발하였습니다.