[CPD][AUC] Model-free Change-point Detection Using ModernClassifiers(by Rohit Kanrar, Feiyu Jiang, and Zhanrui Cai)

https://arxiv.org/abs/2404.06995

Model-free Change-point Detection Using Modern Classifiers

Keypoint

AUC(Area Under the Curve) 를 변화점 탐지에 활용하여, 데이터의 분포 변화 여부를 평가

아래의 과정을 따름 

1. 데이터 분할(Sample Splitting):
   데이터 세트를 세 개의 부분으로 나눕니다: 양쪽 끝의 데이터를 포함한 D0와 D1, 그리고 중간 검증 데이터 Dv.
   D0의 데이터는 vt=0, D1의 데이터는 vt=1의 레이블을 붙입니다.
2. 분류기 훈련(Training the Classifier):
   D0와 D1을 학습 데이터로 사용하여, 분류기를 훈련시킵니다. 이 과정에서 각 관측치 z에 대해 해당 분류기가 포착한 조건부 확률(bθ(z))을 추정합니다.
3. 재귀적 분할(Recursive Splitting):
   다음으로, 중간 데이터 Dv를 여러 부분으로 나누고, 각 후보 변화점에 대해 분류기를 통해 정확도를 측정합니다.
4. 정확도 측정(Measuring Accuracy):
   각 후보 변화점 k에 대해 AUC(Receiver Operating Characteristic curve 아래 면적)를 계산합니다. AUC 값은 k에 따른 두 분포의 구별 가능성을 나타냅니다.
   
   최종적으로, AUC 값의 최대값을 구하여 변화점을 추정하고, 저자들은 이 방법이 완전한 비모수적이며, 강한 가정 없이 높은 차원의 복잡한 데이터에서도 잘 작동한다고 주장

또한 pivoal imiting distribution을 이용하여 이론적 근거도 함께 제시(관련한 내용은 차후에 더 알아봐야할듯)

 

추가적으로 multiple cp 추정은 다음의 프로세스로 이뤄짐

Abstract 

현대 데이터 분석에서는 non-stationary이고 complex 데이터셋을 다루는 경우가 많다. 이러한 데이터셋은 일반적인 저차원 유클리드 공간을 넘어 확장되는 경우가 많아, 강한 구조적 가정을 하지 않고는 데이터 분포의 변화를 탐지하는 것이 어려울 수 있다. 

 

본 논문에서는 Maching learing  분야에서 개발된 classifier 모델을 이용하여 novel offline CPD 방법을 제안한다. Data spliting을 을 통해  테스트 통계량은 연속적으로 계산된 AUC(Area Under the Curve)를 기반으로 구성되며, 이 AUC는 데이터 시퀀스 양쪽 끝의 부분 구간을 학습한 Classifier를 통해 나온 값이다.

 

이 논문에서는 AUC 프로세스가 실제 change point에서 최대값을 가짐을 이론적으로 증명하고, 이를 기반으로 역으로 변화점 추정이 가능함을 보인다. 제안한 방법은 non-parametric하고, 데이터의 기본 분포나 분포 변화에 대한 엄격한 가정을 요구하지 않으며, 높은 범용성과 유연성을 가진다.  

 

이론적으로는 본 논문에서 제안된 test 통계량의 null hypothesis 하에서 limiting pivotal distribution(극한 분포)를 도출하고 local 및 fixed 대립가설하에서 점근적 성질(asymptotic)을 분석한다. 또한 change-point estimator의 약한 일관성도 보장됨을 증명한다. 

실험적으로는 시뮬레이션 연구 및 두개의 실제 데이터셋 분석을 통해, 제안된 방법이 기존의 model-free 변화점 탐지 기법들보다 우수함을 입증하였다. 

 

1. Introduction

본 논문에서는 측정가능한 공간(measurable space)에서 값을 가지는 independent elemnts Zt의 분포 변화를 탐지하는 문제를 풀고자한다.  

이는 아래의 가설검정 문제로 공식화 가능하다. 

 

이때 두 분포 Px와 Py 모두 미지의 확률분포이다. 위와 같은 가설 검정문제는 일반적으로 CPD 문제로 알려져 있다. 

기존의 변화점 탐지 기법들은 종종 분포 Px와 Py에 대한 강한 structural assumption을 가지고 특정한 시나리오에 맞춰 설계되는 경우가 많다. 

예를 들어 기존에 읽었던 금융계열 논문에서는 var변화에 관해 주로 다루었고, 편차를 주로 이용하는 방법론들도 있었음

 

이러한 접근법의 상당수가 고전적인 유클리드 공간에서의 1차 또는 2차 모멘트(moment)에 초점을 맞추거나, 데이터 생성 과정에 대한 모수적(parametric) 가정을 활용한다. 이에 대한 최근 연구들을 살펴보면 Aue & Horváth (2013), Chen & Gupta (2012), Truong et al. (2020) 등이 있다.

 

그러나 현대에서는 복잡한 고차원의 형태의 데이처가 많이 수집되고 있으며, 전통적인 유클리드 공간을 벗어난 특성을 보이는 경우가 많다. 예를 들어, 금융 분석에서는 고차원 주식 데이터를 활용하여 “세계 금융 위기(Great Recession)”와 같은 주요 경제 사건 동안 분포 변화의 원인을 분석할 수 있다 (Chakraborty & Zhang, 2021). 경제 지리학에서는 위성 이미지 데이터를 활용하여 인간 활동이 환경에 미치는 영향을 연구하는 경우가 많다 (Atto et al., 2021). 또한 도시 연구에서는 교통 데이터 분석을 통해 교통 패턴의 변화나 교란을 탐지할 수 있다 (Chu & Chen, 2019).

이러한 사례들은 다양한 데이터 차원과 유형을 수용할 수 있는 보편적인 변화점 탐지 프레임워크를 개발하는 것이 매우 어렵다는 점을 강조한다. 이러한 문제를 해결하기 위해 본 연구에서는 데이터의 차원과 유형에 관계없이 일반적인 분포 변화를 탐지할 수 있는 새로운 변화점 탐지 프레임워크인 changeAUC를 제안한다.

 

1.1 Our Contributions

본 연구에서 제안하는 방법인 changeAUC는 modern classficiation 알고리즘이 high-dimensional two-sample testing(Kim et al., 2021; Hu and Lei, 2023) 및

Kim, I., Ramdas, A., Singh, A., and Wasserman, L. (2021). Classification accuracy as a proxy for two sample testing. The Annals of Statistics, 49(1):411–434. 

Hu, X. and Lei, J. (2023). A two-sample conditional distribution test using conformal prediction and weighted rank sum. Journal of the American Statistical Association, in press

 

 independence test(Cai et al., 2022, 2023)에서 성공적으로 활용된 최근 연구들에서 영감을 받았다. 

 

changeAUC는 다음의 3단계로 구성된다.

1. 데이터 분할(Data-splitting): 양 끝단의 데이터를 절단(trimming)하여 데이터를 분할한다.
2. 분류기 학습(Classifier Training): 말단(terminal) 관측치에 대해 분류기를 학습한다.
3. AUC 기반 테스트(Test Using AUC): ROC 곡선 아래 면적(AUC, Area Under the ROC Curve)을 이용하여 중간 구간의 관측치에 대한 정확도를 평가한다.

classification accuracy test의 핵심 아이디어는 다음과 같다. 만약 두 개의 샘플 그룹이 서로 다른 분포를 따른다면, 복잡한 분류기는 두 분포를 구별할 수 있어야 하며, 테스트 세트에서 높은 분류 정확도를 보일 것이다. 이를 활용하여, 한 번의 분류기 학습 이후 시간 축을 따라 분류 정확도를 측정하며 재귀적으로 이표본 검정을 수행함으로써 변화점 탐지를 가능하게 한다.

제안하는 방법 changeAUC는 다음과 같은 장점을 갖는다.

• 완전한 비모수적 접근법(Completely Nonparametric)
  • 데이터 분포에 대해 어떠한 모수적 가정도 요구하지 않는다.
  • 평균(mean)이나 공분산(covariance)의 변화, 희소(sparse) 또는 밀집(dense)된 변화 등, 변화의 형태에 대한 구조적 가정도 필요하지 않다.
• 높은 범용성(Highly Versatile)
  • 본 방법은 고전적인 저차원 유클리드 데이터부터 고차원 및 비유클리드(non-Euclidean) 데이터(예: 이미지, 텍스트)에 이르기까지 거의 모든 유형의 데이터에 적용 가능하다.
  • 단 하나의 필수 조건은 적절한 분류기의 사용 가능 여부이다.
• 유연한 적용 가능성(Considerably Flexible)
  • 적절한 분류기를 선택함으로써 특정 응용 분야에 맞게 조정할 수 있다.
  • 기존의 도메인 지식(prior knowledge)을 효과적으로 분석에 반영할 수 있다.
  • 예를 들어, 합성곱 신경망(CNN)을 활용하면 이미지나 비디오에서 변화점을 탐지하는 데 사용할 수 있다.
  • 또한, 본 방법은 분류기의 완벽한 정확도를 요구하지 않는다. 두 분포 사이에서 신호를 일부라도 포착할 수 있다면 변화점 탐지가 가능하다.
• 분포 독립적 접근법(Distribution-Free)
  • 귀무가설(null hypothesis) 하에서 검정 통계량(test statistic)이 pivotal limiting distribution를 가진다.
  • 브라운 운동(Brownian motion)의 함수적 형태로 표현될 수 있으며, 따라서 유의값(critical values)을 수치적으로 계산하여 활용할 수 있다.

​Pivotal Limiting Distribution: 귀무가설 아래에서, 통계량은 특정 통계적 성질을 갖는 분포로 수렴할 때 해당 분포를 피벗 한계 분포라고 함

 

본 연구에서는 제안된 방법에 대한 엄밀한 이론적 분석을 수행하였다.

• 경험적 과정 이론(Empirical Process Theory)(Vaart & Wellner, 2023)을 이용하여 귀무가설 하에서 검정 통계량의 pivotal limiting distribution 를 유도하였다.
• 검정 통계량의 점근적(asymptotic) 성질을 국소(local) 및 고정(fixed) 대립가설 하에서 도출하였다.
• AUC 과정의 극댓값(maximizer)의 약한 일관성(weak consistency)을 보장하여 추정(estimation)의 안정성을 확인하였다.

추가적으로, 시뮬레이션 데이터 및 두 가지 실제 데이터(real-world applications)를 활용한 실험을 시행 그 결과, 본 방법이 유의수준(size) 조절을 효과적으로 수행할 수 있음을 확인하고, 기존의 변화점 탐지 방법들과 비교하여 경쟁력 있는 검정력(power)을 보유함을 입증하였다.

 

1.2 Related Work

1.2.1 Offline CPD 

Offline change point detection의 시작은 Page(1954)의 연구로, 변화점 문제를 해결하는 전통적인 접근법은 일반적으로 평균이나 분산과 같은 저차원 변수 또는 특정한 모수적(parametric) 모델에 한정되는 경우가 많다. 이에 대한 포괄적인 검토로 Aue & Horváth(2013), Chen & Gupta(2012), Truong et al.(2020)을 참고할 수 있다. 

 

현대에는 고차원 데이터 및 비유클리드 데이터가 다양한 분야에서 다루어지게 되었다. 

특히, 고차원 데이터와 관련하여 많은 연구가 평균 변화(mean changes)에 집중되었으며, 이에 대한 연구로 Jirak(2015), Cho & Fryzlewicz(2015), Wang & Samworth(2018), Enikeeva & Harchaoui(2019), Yu & Chen(2020), Wang et al.(2022) 등을 들 수 있다. 또한 공분산 변화(covariance changes)에 대한 연구로 Avanesov & Buzun(2018), Steland(2019), Dette et al.(2022), Li et al.(2023) 등이 있으며, 그 외의 모델 매개변수 변화에 관한 연구로 Kaul et al.(2019), Liu et al.(2020) 등이 있다.

 

비유클리드 데이터의 경우, 힐베르트 공간(Hilbert space)에서의 연구가 활발히 이루어졌으며, 함수형 평균 변화(functional mean changes)에 대한 연구로 Berkes et al.(2009), Aue et al.(2018), 함수형 공분산 변화(functional covariance changes)에 대한 연구로 Jiao et al.(2023)을 언급할 수 있다. 또한 Dubey & Müller(2020), Jiang et al.(2024)은 거리 공간(metric space)에서의 1차 및 2차 모멘트 변화 탐지(change-point detection)에 대한 최신 연구를 제시하고 있다. 위에서 언급된 연구들은 주로 한두 가지 특정 유형의 변화를 탐지하는 데 초점이 맞춰져 있으며, 데이터의 다른 측면에서 변화가 발생할 경우 탐지 능력이 부족할 수 있다. 이러한 한계를 인식한 최근 연구에서는 보다 일반적인 변화 유형에 대해 강력한 비모수적(nonparametric) 방법이 많은 주목을 받고 있으며, 대부분 저차원 유클리드 공간을 대상으로 연구가 이루어졌다(예: Harchaoui & Cappé, 2007; Matteson & James, 2014; Zou et al., 2014; Arlot et al., 2019).

 

고차원 데이터와 관련된 연구는 아직 많지 않으며, 최근 연구로는 Chakraborty & Zhang(2021)이 일반화된 에너지 거리(generalized energy distance) 개념을 도입한 바 있다. 그러나 이 방법은 고차원 데이터에서 주변 분포(marginal distributions)의 pairwise homogeneity( 대립가설 H₁ 하에서 heterogeneity )만을 포착할 수 있어, 두 분포 PX​ 와 PY 가 동일한 주변 분포를 가지지만 다른 측면에서 차이를 보이는 경우 탐지 능력이 부족할 수 있다.

 

또한, 최근 Chen & Zhang(2015), Chu & Chen(2019)에 의해 그래프 기반(graph-based) 검정이 제안되었으나, Chakraborty & Zhang(2021)이 지적한 바와 같이 이 방법들은 고차 모멘트(higher-order moments)의 변화를 탐지하는 데 한계가 있을 수 있다.

 

머신러닝 기법을 활용하여 이표본 검정(two-sample testing) 및 변화점 탐지(change-point detection) 문제를 해결하려는 최근 연구들은 아래와 같다. Kim et al.(2021) 이후, 분류기(classifier)를 이용한 이표본 검정 방법이 활발히 연구되고 있으며, 관련 연구로 Lopez-Paz & Oquab(2016), Kim et al.(2019), Kirchler et al.(2020) 등을 들 수 있다. 그러나 변화점 탐지 문제로의 확장은 아직 충분히 연구되지 않았으며, 예외적으로 Lee et al.(2023), Londschien et al.(2023), Li et al.(2024)에서 일부 논의된 바 있다.

특히, Lee et al.(2023)은 온라인(online) 변화점 탐지를 위해 신경망(neural networks)을 적용하였으며, Londschien et al.(2023)과 Li et al.(2024)는 본 연구와 마찬가지로 오프라인(offline) 변화점 탐지에 초점을 맞추었다. Londschien et al.(2023)은 분류기 기반 비모수적 우도비(nonparametric likelihood ratio)를 도입하여 랜덤 포레스트(Random Forest) 기법을 활용한 변화점 탐지 방법을 제안하였으며, Li et al.(2024)는 지도학습(supervised learning) 환경에서 시계열 변화점을 탐지하기 위해 신경망을 적용하였다.

Londschien, M., Bühlmann, P., & Kov'acs, S.T. (2022). Random Forests for Change Point Detection. 
J. Mach. Learn. Res., 24, 216:1-216:45.

Lee, J., Xie, Y., & Cheng, X. (2023). Training Neural Networks for Sequential Change-Point Detection. ICASSP 2023 - 2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 1-5.

 

 

본 연구에서 제안하는 접근법은 classifier를 이용하였고, 아래와 같은 부분에서 차이를 보인다. 

1. 앞서 언급된 방법들은 암묵적으로 저차원 데이터를 가정하고 있지만, 본 연구의 접근법은 고차원 데이터뿐만 아니라 비유클리드 데이터까지 처리할 수 있도록 확장되었다.
2. 기존 연구들은 점근적(asymptotic) 분석을 제공하지 않기 때문에, 검정 과정에서 순열(permutation) 기반 접근법을 사용해야 하거나 보수적인 1종 오류(type-I error) 제어를 필요로 한다. 반면, 본 연구에서는  pivotal limiting null distribution을 기반으로 한 점근적 방법을 제공하여 실질적인 통계적 추론을 용이하게 한다. 따라서, 본 연구는 특히 이론적인 측면에서 기존 연구들을 보완한다.
3. Londschien et al.(2023)의 비모수적 우도 접근법과 Li et al.(2024)의 empirical risk minimizer기반 분류 정확도 측정 방식과 달리, 본 연구에서는 분류 정확도를 AUC(Area Under the Curve)로 측정한다. AUC는 순위 합(rank-sum) 기반 방법이므로, 불균형한 데이터 분할(imbalanced data splits) 및 학습이 충분하지 않은 분류기(weakly trained classifiers)에 대해서도 보다 강건한 결과를 제공할 수 있다.
4. Gao et al.(2023)에서 제안한 데이터 분할(data-splitting) 방식과 유사한 접근법을 취한다. 이 연구에서는 변화점을 탐지하기 위해 중간 관측치를 양 끝단의 관측치에 의해 결정된 방향으로 투영하여 차원에 무관한(dimension agnostic) 변화점 검정 통계를 제안하였다. 그러나 해당 방법은 평균 변화(mean change) 탐지만을 목적으로 하며, 본 연구에서 제안하는 방법은 보다 일반적인 접근법을 취하고 AUC 기반 순위 합 비교(rank-sum comparison)를 활용한다.

2. Methods

2.1장에서는 단일변화점추정(single CPD) 문제를 푸는 changeAUC를 설명한다.
2.2장에서는 changeAUC의 각 단계에 대한 상세한 정의를 제공한다.
2.3장에서는 changeAUC를 확장하여 다중 변화점 추정(multiple CPD)에 적용하는 방법을 다룬다.

2.1 Proposed Method

독립적인 random elements Zt가 확률공간 (Ω,F, P)에서 정의되며, 가측 공간인 (E, e)에서 값을 가진다고 하자(기본가정, intro 참고). 그리고 Px와 Py가 동일한 확률공간에 정의된 서로 다른 확률 분포이다. 

또한 해당 확률 분포는 

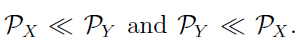
라고 하자(are absolutely continuous with respect to other, 쉽게 풀어쓰면 P가 0인 집합 혹은 사건에 대해 Q도 0이 되는 성질)

 

그럼 단일 변화점  추정 문제에서 가설검정은 1.1에서 밝힌것과 같이 아래로 정의된다. 

 

본 논문에서 제안하는 방법론은 다음 4가지 단계로 구성된다. 

1. 샘플 분할(Sample Splitting):
작은 분할(trimming) 매개변수 𝜖 ∈(0,1/2)에 대해 m=⌊Tϵ⌋로 설정하고, 관측값을 세 부분으로 분할한다.

즉, D0와 D1은 𝜖 비율만큼을 전체 데이터에서 가진다

2. 분류기 학습(Training Classifier):
D0의 샘플에는 레이블 vt = 0, D1의 샘플에는 vt=1을 할당한다(즉, 두 샘플이 서로 다른 확률분포를 가진다고 가정한다)

이후 이 양끝의 데이터 샘플을 모두 이용하여서 classifer을 학습한다. 

classfier model과 관련한 조건부 확률분포의 모수를 θ(·)라고 하자. 즉, 새로운 관측값 z에 관하여, 아래의 확률분포는 z가 D1을 따르는 분포(v=1임으로)에서 나왔을 확률을 추정한 값이다. 

3. 재귀적 분할(Recursive Splitting):

이제 새로운 분할 매개변수 η ∈(0,1/2−ϵ) 에 대해 후보 change point 집합을 아래와 같이 정의한다. 

 

즉 후보 집합은 변화점이 될 가능성이 높은 중간 영역에서 후보 지점(k)를 선택하는 것이다. 

 

해당 후보 cp 집합에 속하는 k에 관하여 validation set을 아래와 같이 두가지로 나눈다.

즉. 후보 k의 앞 뒤로, 중간부분의 데이터를 재분할한다.  

4. 정확도 측정(Measuring Accuracy):
AUC 측정을 휘애 각 k에 관하여 k의 전부분에 해당하는 샘플에는 vt=0을 뒷부분에 해당하는 샘플에는 vt=1을 할당하고, 다음과 같이 ROC curve 아래의 면적, 즉 AUC를 계산한다.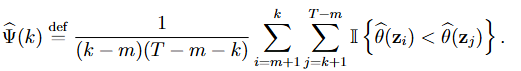 

 

즉, k번째 후보 변화점에서의 AUC값은 우와 같이 정의되며, 변화점 이전 샘플 zi가 이후 샘플 zj보다 작을 확률(작으면 I가 1)을 계산한다. 이를 통해 모든 후보 변화점에 대해 해당하는 AUC 점수의 집합

을 얻는다. 

 

Remark 1. The choices of ϵ and η are subjective

triming 하이퍼파라미터의 선택은 주관적이다.

ϵ에 관해:   ϵ을 너무 작게 선택하면 검정력(power)이 감소할 수 있으며, 반면 ϵ을 너무 크게 설정하면 변화점이 시퀀스의 중앙 근처에 존재해야 한다는 제약이 생기기 때문에 적절한 학습을 위해 값을 잘 선택해야한다. 

실제로 논문에서는 이 값을 0.15로 고정할것(즉 3:7 비율)을 제안한다. 그러나 샘플 크기가 너무 크거나 분류기가 샘플이 더 작은 상황에서도 잘 작동하는 경우 더 작게 설정하는 것도 가능하다. 

 

η에 관해: 

η는 변화점 검정 문헌에서 일반적으로 사용되는 매개변수이다(Andrews, 1993 참조). 본 논문에서는 해당값을 0.05로 고정할 것을 제안한다. 

직관적으로 귀무가설 H0하에서 변화점이 존재하지 않으면 추정된 AUC값은 모든 k에 대해 0.5에 가까울 것이며(무작위로 선택하는 것과 동일), H1 하에서는 실제 cp인 t0 근처의 k에서는 0.5보다 큰 값을 가질 것으로 예상되며 분류에 도움을 줄것이라고 예측할 수 있다. 따라서 검정통계량은 최대 AUC 값을 선택하여 정의된다. 

또한 최댓값을 이루는 지점인

을 변화점 추정값으로 사용한다. 

 

즉, Qt의 값이 충분히  크다면 귀무가설 H0를 기각한다. 

 

3장에서는 귀무가설 H0 하에서 통계량 Q의 점근적 성질을 분석하여 적절한 스케일링을 통해 pivotal process에 약하게 수렴함을 보인다.

 

이때 G()는 standard Brownian motion의 pivoal function이고 γ=ϵ+η이다. 

 

따라서 이론적 quantile(분위수)를 시뮬레이션 하여 H0를 검정 가능할 것이다. 

G0​(r)의 상위 100(1−α)% 분위수를 Q(1−α)라 하면, 100,000번의 몬테카를로 시뮬레이션을 통해 Table 1에서 α=20%, 10%, 5%, 1%, 0.5%에 대한 Q(1−α) 값을 제공한다.

결과적으로, 단일 변화점을 탐지하기 위한 유의수준 α의 검정은 다음 조건을 만족할 때 귀무가설 H0를 기각한다.

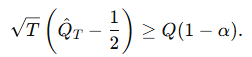
2.2 Classification Accuracy for Detecting a Single Change-point

 

실제로 Px, Py, t0(real change point) 모두가 알려져 있지 않다. CP에 관한 통계적 가설검정(1.1)을 검정하기 위해서는 두 분포를 구별하는 것이 중요하다. ChangAUC 알고리즘의 특징은 두개의 알려지지 않은 분포의 이질성(heterogeneity)를 식별하기 위해 적절한 분류기를 학습시키는 것이다. 따라서 우리는 모델의 θ(·)를 실제 조건부 분포의 확률과 동일하다고 하자.

만일 Px와 Py에서 무한개의 샘플이 추출되고, 각 샘플이 올바르게 v=0 혹은 v=1으로 라벨링이 되었을 때 실제 조건부 확률을 얻는 것이 가능할 것이다. 

여기서 z는 새로운 관측값이다. 

또한  θ(·)은 참 likelihood ratio와 관려되어 있으며 이는 아래와 같이 서술된다. 

이제 L(z), 즉 관측 값z에 관한 우도비를 확인하자. 

만일 Px = Py라면 거의 L(z)는 1에 가까울 것이다. 아니라면 L(z)는 z가 Py에 속할 때는 크거나 혹은 역일것이다. 그럼으로 L(z) 혹은 동일한 선에서 θ(z)는 관측값 z의 1차원 투영으로 기능한다. 아래의 Propostion 1은 이러한 투영과 두 분포간의 total variation간의 관계를 주장한다. 또한 이는 heterogneity를 판정하기 해 rank-sum comparison of liklihood를 사용하는 동기를 제공한다.

 

Probaility measuer: 수학적 확률론에서 사건의 발생 가능성을 수량화하는 함수로 정의, 표본공간 내의 사건과 확률 맵핑하는 역할

 ​Radon-Nikodym funtion:  측도론에서 두 확률 측도 사이의 관계를 나타내는개념. 이는 한 측도가 다른 측도에 대해 절대 연속일 때, 그 두 측도의 비율을 나타내는 함수로 정의된다. 

 

Proposition 1 공통 확률 공간 (Ω, F, P)에서 두 확률 측도 Px와 Py를 생각하자.  이때 Py << Px 이며, Radon-Nikodym funtion 이 Px하에서 연속인 확률공간이다. 

Z1 ~ Px이고 Z2 ~Py인 독립 랜덤 변수라고 하면, 아래를 따른다. 

 

여기서 dtv()는 Px와 Py간의 총 변동거리를 말한다. 

 

두 확률 분포 간의 총 변동 거리(total variation distance)가 유의미하게 크다면, (2.3)에서의 확률에 대한 경험적 추정값이 PX와 PY 간의 이질성을 효과적으로 포착할 것으로 예상된다. 이와 관련하여, (2.3)에서의 확률이 가능도 비율(likelihood ratio) 

 

를 포함한다는 점이 주목할만하다(notworthy). 

 

저차원 유클리드 데이터의 경우, L(·)을 직접 추정하는 것이 일반적이다. 그러나 고차원 유클리드 데이터에서는 차원의 저주(curse of dimensionality)로 인해 가능도 비율을 직접 추정하는 것이 어렵다. 대신, (2.2)에서 일관된 추정값 θ(·)을 대입하여 L(·)을 추정하는 것이 가능하며 이는 2.4와 같다. 

 

2.2와 수식이 반대다

 

외부 데이터셋을 활용하여 지도 학습(supervised setting) 하에서 조건부 확률 추정값 θ^(⋅)을 얻는 것이 가능하다는 점은 주목할 만하다 (Li et al., 2024). 그러나 본 논문에서는 이러한 외부 데이터셋이 존재하지 않는다고 가정하는 비지도 학습(unsupervised setting) 환경을 가정하기에 과적합(over-fitting)의 위험을 완화하기 위해 보다 실용적인 해결책으로 데이터 분할(data-splitting)을 제안하며, 학습 데이터셋의 관측값

을 이용하여 θ^(⋅)을 얻는다. 

너무 naive한 비지도 학습아닐까....? 싶다 나누는 기준이 애매하고 Px를 따른다는 보장이 있나?

 

또한 validation Datset Dv를 활용하여 

Px와 Py 두 분포간의 차이를 평가한다. 

 

변화점 탐지(change-point detection) 문제에서 변화 발생 시점 t0​는 일반적으로 알려져 있지 않으며, 이는 기존의 지도 학습 분류 문제와 달리 검증 데이터 DvD_vDv​가 레이블되지 않았음을 의미한다. 이러한 문제를 해결하기 위해, Dv를 반복적으로 분할하여 추정된 liklihood ratio에 관하여 two sample rank sum을 제안한다. 

 

이는 평균 오분류 오류(average misclassification error)에 대한 견고한 대안이 되고, 3장에서, 순위 합 비교를 활용하면 일관된 θ^(⋅)추정이 필수적이지 않다는 점을 설명한다(Remark 2 참조).

 

추정된 가능도 비율의 두 표본 순위 합 비교는 학습된 분류기의 AUC(Area Under the Curve)와 동등하다(Fawcett, 2006; Chakravarti et al., 2023). 특히, 각 변화점 후보 k에 대해 검증 데이터를 기반으로 하여 

일때, 

를 얻을 수 있다. 

 

해당 수식을 조금 더 자세히 살펴보자. 
우선 첫번째 등호 식에서 1/(k-m)(T-m-k) 항은 정규화항이다. 

두번째 등호에서 I항안에 분수식은 각각의 z가 특정 확률에 속할 확률을 의미한다. 
마지막 등호에서 이는 각각의 데이터 포인트에 대한 우도비로 변환된다. 

즉 변화점 이전과 이후의 데이터 샘플을 비교하여 변화가 존재하는지 판단하는 지표로 사용된다. 이는 기본적인 AUC  수식에서 확률값을 logit transformation을 통해 logit으로 변환한다(이는 x∈(0,1)에서 단조 변환(monotone transformation)임을 이용하여 성립). 마지막으로 log-odd는 단조 증가 함수이기에 마지막 등호 식과 같이 단순화가 가능하다. 

 

주목할 만한 점은 Px와 Py가 동일하다면 추정된 log ration 비율인 L은 1에 가까울 것으로 예측되며 이로 인해 Ψ^(k) 또한 0.5에 가까워진다는 것이다. 

 

추정된 확률의 순위 합 비교(rank-sum comparison), 즉 AUC를 사용하는 결정을 정당화하기 위해 몇 가지 추가적인 논의를 제공한다. 이는 raw class probabilities이나 평균 오분류 오류(average misclassification error)와 같은 일반적으로 사용되는 지표를 사용하는 대신 선택된 방법이다.

Rank Sum 비교 (Rank Sum Comparison): Rank Sum 비교는 두 개의 확률 분포의 차이를 평가하는 통계적 방법으로. 주로 비모수적 방법으로 사용되며, 정확하게 두 개의 샘플을 비교하는 데 유용합니다. 즉, 데이터의 분포가 비대칭이거나 비모수적일 때 유용하다.  두 확률 분포가 주어졌다는 가정하에 Rank Sum 비교는 각 분포에서 샘플을 가져와 그들의 순위를 매긴 후, 그 순위의 합을 사용한다
간단히 Kruskal wallis 검정을 생각하면 될듯! 

 

Remark 2.

AUC는 a rank sum comparison와 관련되어 추가적인 장점을 제공합니다. 우리 프레임워크는 변화점의 위치를 정확하게 추정하는 데 뛰어난 성과를 나타냅니다. t0에 단일 변화점이 있을 경우, 조건부 확률 집합

 

가 뚜렷한 차이를 보일 때 정확한 추정(precise estimation)이 이루어집니다.

일반적으로 일관된 분류기를 학습하여 얻는 것처럼 이 집합들이 각각 0과 1에 가까워야 하는 접근법과 달리(즉 명확한 분류가 되어야하지만), 우리 프레임워크는 그러한 조건이 엄격히 충족되지 않더라도 강력한 성능을 보입니다. 

 

Remark 3. 

AUC의 또 다른 장점은 심각한 클래스 불균형이 있는 두 샘플 분류에서의 강건한 성능입니다. 자세히는 changeAUC의 step 4를 보면,  여기서 추정된 클래스 확률 집합 θ^이 AUC 집합 Ψ^를 도출하는 데 사용됩니다.

η가 작게 선택될 경우, Dv0 및 Dv1는 k가 Icp의 시작이나 끝에 가까울 때 심각한 불균형을 이루는 두 개의 관찰 집합을 형성합니다(즉 두 val의 균형이 맞지 않음). 이러한 경우, t0가 Icp의 중간에 가깝지 않다면 AUC를 사용하는 것이 보다 강력한 대안임을 입증합니다. t0 근처에서의 더 높은 정확도는 Kim et al. (2021)에서 제안한 고정 임계값, 예를 들어 1/2와 비교했을 때 평균 잘못 분류 오류와 관련이 있습니다.

 

2.3 Extension to Multiple change-points:

IPSS 방법이랑 동일, 즉 여러번 반복수행하는 방식 자세한건 아래의 글 참고

 

changeAUC는 다중 변화점을 추정하기 위해 설계된 기존 알고리즘과 통합하는 것이 가능하다. 예를 들어, 와일드 이진 분할(Wild Binary Segmentation, WBS) (Fryzlewicz, 2014), 시드 이진 분할(Seeded Binary Segmentation, SBS) (Kovács et al., 2023), 단일 변화점 탐지(Isolating Single Change-Points) (Anastasiou & Fryzlewicz, 2022) 등이 있다.

 

본 논문에서는 5장에서 두 개의 실제 데이터셋을 분석하기 위해 다중 변화점 추정 방법으로 Seeded Binary Segmentation, SBS를 활용한다.

 

SBS 절차는 다음과 같이 진행된다. 길이가 T인 시계열에 대해, SBS는 사전에 정의된 구간 집합 Iλ(cp의 후보군)​에서 단일 변화점 검정 통계를 반복적으로 적용한다.

 

이때 Iλ는 다음과 같다. 

 

여기서 λ ∈ [1/2, 1)는 감소 파라미터(decay parameter)이며, 각 Ik는 길이

인 다수의 sub-interval들의 집합이며, 이들은 다음과 같이 균등하게 이동한다.

 

SBS는 모든 부분 구간에서 계산된 검정 통계값 중 최대값을 찾고, 이를 사전에 설정된 임곗값 Δ와 비교한다. 최대 검정 통계값이 Δ을 초과하면, 해당 시점에서 변화점이 존재한다고 판단한다. 이후 데이터를 두 개의 부분집합으로 나눈 후 동일한 절차를 각각 적용한다(즉 찾고 그 안에 더있나 찾기)

한편, Kovács et al. (2023)은 평균 변화점 탐지(mean change-point detection) 문제만을 다루었다. 따라서 이들의 임곗값 Δ은 changeAUC를 해당 알고리즘에 통합할 때 그대로 적용되기 어려우며, 평균뿐만 아니라 분포 전체에 걸친 다중 변화점 탐지를 위한 새로운 이론적 개발이 필요하다. 본 논문에서는 이러한 확률 제어(type-I error control)에 대한 연구를 추후 과제로 남긴다.

대신, Dubey & Zheng (2023)이 제안한 방법을 따라, 변화점 검출을 위한 임곗값 Δ을 결정하기 위해 순열 검정(permutation test)을 수행한다. 알고리즘 2는 이 접근법의 절차를 개략적으로 설명한다. 실용적인 구현에서는, 순열 검정으로 얻은 최대 검정 통계량의 영분포(null distribution)에서 90% 분위수(quantile)를 선택하여 Δ로 설정하며,

감소 파라미터는 아래와 같다. 

1.변화점 탐지: 먼저 전체 데이터에 대해 변화점을 찾습니다. 2.구간 나누기: 발견된 변화점을 기준으로 데이터를 두 개의 서브 구간으로 나눕니다. 3. 반복: 각 서브 구간에 대해 알고리즘을 다시 실행하여 그 안에서 추가적인 변화점을 탐지합니다.

3. Theoretical Justification

Null distribution: 특정한 가설이 참일 때의 통계량의 분포를 나타냅니다. 
정의: 귀무 가설(H0) 하에서의 검정 통계량의 분포를 지칭합니다. 이는 검정 과정에서 영 가설을 기반으로 하여 통계량의 '한계' 행동을 설명합니다.
목적: Null 분포를 통해 통계량의 분포를 이해하면, 이를 이용해 연구자가 설정한 임계값을 결정하는 데 도움을 줍니다. 이는 특히 통계적 추론과 유의성 검정에서 중요합니다

 

이 절에서는 changeAUC의 이론적 특성을 분석한다.

3.1절에서는 검정 통계량의 제한 영분포(limiting null distribution)를 도출하여 (2.1)에서의 주장에 대한 정당성을 제공한다.

3.2절에서는 고정 대립가설(fixed alternative) 및 국소 대립가설(local alternative)에서의 검정력(power) 특성을 제시한다. 

3.3절에서는 변화점 추정량 R^T\hat{R}_TR^T​의 약한 일관성(weak consistency) 성질을 다룬다.

 

이론적 결과를 제시하기에 앞서, 몇 가지 필요한 표기법을 정의한다.

우리는 P∗,E∗,Var∗,Cov*를 학습된 분류기(trained classifier)와 학습 데이터 D0∪D1​가 주어졌을 때의 조건부 확률, 기댓값, 분산, 공분산으로 정의한다.

임의의 랜덤 원소 Z∈E 에 대해, Z∼Px일와 ~Py 때의 조건부 누적분포함수(CDF)를 각각 다음과 같이 정의한다.

 

또한, random 원소인 Z에 관하여 모든 t=1...T에 관해 w를 Z의 CDF 값으로 정의한다. 

마지막으로 람다는 다음과 같다. 

 

3.1 Limiting Null Distribution

하기의 검정통계량 Q가 귀무가설 H0 vs H1에서 나온것임을 다시금 생각해보자. 

 

적절한 scaling하에서 AUC의 극한 성질(limiting behavior)을 연구하는 것은 일반적인 과정이다. 

 

정리 1에서 

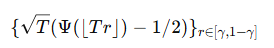
가 조건부 확률 측도 P*하에서 uniformly하게 pivotal process(중심과정)으로 수렴함을 보인다. 

 

 

Theorem 1에서 G는 표준 브라운 운동의 함수이며, 이는 분류기(classifier), 데이터 차원(data dimension), 또는 데이터 분포(data distribution)에 의존하지 않는다. 따라서, 이 이론적 극한 분포의 시뮬레이션된 분위수를 이용하여 계산적으로 효율적이면서도 통계적으로 타당한 검정 프레임워크를 제안할 수 있다(2.1에서의 표 1 참조).

 

추가적으로 θ는 연속이라는 가정 외에 일관되게 추정될 필요는 없다. 즉 귀무가설 하에서 무작위 추정(random guess)도 적용가능하다. 연속이라는 가정은 , 이는 로지스틱 회귀(logistic regression), 랜덤 포레스트(random forest), 심층 신경망(deep neural networks)과 같은 일반적으로 사용되는 분류기들에 대해 보통 만족된다. 만약 특정 지점에서 점 질량(point mass)이 존재한다면, 무작위 동점 처리 방식(random tie-breaking ranking scheme)을 통해 해당 이론의 성립을 유지 가능하다. 

point mass: 이산 확률 변수가 특정 값에서만 양의 확률을 갖고, 나머지 값에서는 0의 확률을 갖는 경우를 말함

 

3.2 Uniform Weak Convergence Under Local and Fixed Alternative

최대 하나의  cp를 가지는 대립 가설 하에서 검정의 극한 성질을 보자. 

True cp를 t0라고 하고, t0 = ⌊τ T ⌋라고 하고 τ ∈ [γ, 1 − γ]라고 하자. 

 

그럼 관측된 랜덤 요소 z는 다음과 같은 설정에서 생성된다(즉 t를 기점으로 분포가 변함)

 

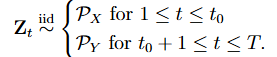
이전 2.2 에서 정의한 우도비(lielihood ratio)를 보면 

Px, Py의 총변동거리와 우도비의 관계를 알 수 있고, 이는 H1이 H0에서 얼마나 벗어났는지를 설명한다. 

 

 Proppstion 2는 두개의 확률 측도에 관해 두 확률 분포 사이의 Total Variation Distance (TV Distance)와 기대값 δ(서로 다른 관측값의 우도차이)가 서로 선형 관계를 가진다는 점을 보여준다. 

 

또한 δ = 0은 ifof 오직 우도비 L()이 상수 측도함수일 때이며, 이는 Px = Py일 때이다(대부분, 거의). 따라서 δ는 대립가설이 H0에 비해 얼마나 벗어나는지 측정하는 지표로 사용가능하다. 

 

Section 3.2.1에서는 fixed alternative하에서, 3.2.2는 local alternative 하에서 bQT의 limiting distribution을 분석한다. 

Fixed alternative: 귀무 가설과 명확하게 다른 특정한 대립 가설을 설정하는 것을 의미하며 특정한 값으로 설정됨. 표본 크기가 증가함에 따라 검정력(power)이 증가

 Local alternative: 통계적 가설 검정에서 대안 가설이 샘플 크기에 따라 점진적으로 변화하는 방식으로 설정되는 경우. 이는 대안 가설이 고정된 값이 아닌, 샘플 크기에 따라 점진적으로 변화하는 형태로 정의, 표본 크기가 증가함에 따라 점점 작아짐

 

3.2.1 Fixed Alternative

 

Assumption1 에서 u*은 실제 데이터 z, 변화점 전후의 샘플을 모델의 예측값인 θ를 이용하여 비교할때, Zx가 Zy보다 작을 확률, 즉, y로부터 유래되었을 확률이다. u는 실제, 즉 이론적인 확률값의 차이이다. 

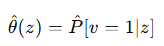
 δ, 3.2d에서 정의한 두 Zx의 우도차의 기대값이 충분히 크다면 이 둘의 차이인 apporoximation error는 무시할 수 있을 만큼 작아야한다. 이 조건이 성립하면 변화점을 안정적으로 탐지할 수 있다. 

 

여기서 중요한 점은 분류기가 반드시 완벽히 훈련될 필요 없다는 것이다. 즉, 머신러닝 분류기의 예측 오차가 존재해도 변화점 탐지가 가능해야 한다는 것이며 이는 기존 변화점 탐지 기법과의 중요한 차이점이다. 

 

이는 θ^가 원래의 θ 값과 정확히 일치할 필요는 없지만, 단조성(monotonicity)을 유지(즉, 데이터 간 상대적 순서 정보(크고 작음의 관계)가 유지)되면 충분하다. 이는 Section2,2에서 논의된것과 같으며 Remark2에서 재강조되었다. 

 

Theorem 2는 Assumption 1이 성립하는 경우 & 샘플 T가 충분히 크면 δ도 작지 않음 , 검정 통계량 Ψ^(k)가 0.5에서 멀어지며, 변화점을 확실히 구별할 수 있음을 보인다. 

 

3.2.2 Local Alternative

 

Assumption2는 Assumption1보다 강한 조건을 요구하며, 이는 (1)에서의 Monotonicity Preservation (단조성 유지) 조건이다. 

이전 Assumption 1에서는 분류기가 단조성을 "대략적으로" 유지하는 것만 요구했지만, Assumption 2에서는 일관되게 유지해야 함을 의미한다. 또한 T가 증가하면 증가할 수록 예측 순서와 실제 순서의 차이가 사라져야한다. 

Assumpion2의 2번째 조건은 분류기의 근사오차(u*-u)가 T-1/2보다 빨리 감소해야한다는 조건이다. 이의 super consistency는 분류기 자체가 아니라 조건부 확률의 rank에 대한 expected monotonicity에 적용된다. 

 

유사 가정들이 독립성 검정(Theorem 7 in Cai et al. (20237) 및 두 표본 조건부 분포 검정(Proposition 1 in Hu and Lei (2023)에서 활용되고 검증된 바 있다

 

Theorem 3에서는 Assumption 2가 성립하는 경우, 변화점 탐지가 더욱 엄밀하게(더 작은 변화도 찾을 수 있음) 이루어진다는 점을 보인다. 

즉, Assumption 2가 성립하면, 변화점이 존재할 때 검정 통계량이 귀무가설(변화점 없음)과 점점 차이가 커진다는 것이다. 

 

3.3 Weak Consistency( 변화점 탐지 방법이 수렴성을 가진다는 점을 수학적으로 보)

논문의 주요 목표는 단일 변화점(change point)에 대한 검정 프레임워크를 제안하는 것으로, 시뮬레이션 연구에서 관찰된 localization performance에서 착안하여 변화점을 추정하는 방법으로

를 이용할 때 weak consistency 결과를 확립한다. 

 

이를 위해 Assumption 3를 도입한다. 이는 독립적인 랜덤 원소인 Z들에 관하여 평균 근사 오차인 u*-u가 확률적으로 0에 수ㄹ렴한다는 의미이다. 

가정 1에서는 검정력이 충분하도록 하기 위해 분류 오차가 일정한 오류 한계를 갖는 것만 요구하지만, 정확한 추정을 위해서는 이 오류 한계가 점근적으로 사라져야 한다는 점이 중요하다. 

 

Therem 4에 관하여 변화점의 상대적 위치( 추정한 변화점 R^TT​ 와 실제 변화점 t0 간의 거리 비율이 0으로 수렴)에 대한 일관성이 보장된다. 본 논문의 프레임워크는 완전히 비모수적(nonparametric)이므로, 명시적인 지역화 속도를 도출하는 것은 어려운 문제이며, 이는 향후 연구 과제로 남겨둔다.

즉, "변화점이 있다"는 것만 아는 것이 아니라, "변화점이 정확히 어디에 있는지"를 알아내는 것이 지역화(Localization) 임

4. Numerical Simulations

이 섹션에서는 제안된 방법의 finite 샘플 성능을 분석한다. 특히, 고차원 유클리드 데이터에 대한 성능은 4.1절에서 조사하며, 비유클리드 데이터에 대한 성능은 인공적으로 생성된 CIFAR10 데이터베이스 이미지(Krizhevsky et al., 2009)를 활용하여 4.2절에서 제시한다.

4.1 High Dimensional Euclidean Data

이 섹션에서는 고차원 유클리드 데이터에서 제안된 검정의 크기 및 검정력 성능을 분석한다. 검정을 수행하기 위해 다음과 같이 요약된 세 가지 분류기를 적용하였다.

• 정규화된 로지스틱 회귀 (Logis): LASSO 패널티를 적용한 정규화된 로지스틱 분류기를 사용한다. Logis는 R 패키지 glmnet(Friedman et al., 2010)을 이용하여 구현하였다.
• 완전연결 신경망 (Fnn): 세 개의 은닉층, ReLU 활성화 함수, 이진 교차 엔트로피 손실을 갖는 완전연결 신경망을 사용한다. 또한, 각 층에 LASSO 패널티를 적용하였다. Fnn은 Python 프레임워크 Tensorflow(Abadi et al., 2016)를 사용하여 구현하였다.
• 랜덤 포레스트 (Rf): 각 트리의 최대 깊이가 8인 200개의 트리를 갖는 랜덤 포레스트 분류기를 사용한다. R 패키지 randomForest(Liaw and Wiener, 2002)를 이용하여 Rf를 구현하였다.

 

크기 성능을 비교하기 위하여 data 생성과정에 있어서 아래를 고려하였다. 

• T ∈ {1000, 2000}: sample의 수 
• p ∈ {10, 50, 200, 500, 1000}: 차원 수

 

Table 2는 5% 유의수준에서 1000번의 반복 실험을 통해 얻은 경험적 기각률을 나타낸다. 결과에 따르면, 고려된 모든 분류기들이 모든 설정에서 제1종 오류를 성공적으로 제어함을 확인할 수 있다.

 

다음으로, 고차원 설정에서 검정력 성능을 분석한다. 변화점 위치는 t0=⌊T/2⌋로 고정하며, 데이터 길이 T=1000 데이터 차원 p∈{500,1000}으로 설정하였다. 변화점 이전의 데이터는 다음과 같이 생성된다.

 

분포 변화의 경우, 변화점 이전과 이후의 데이터는 동일한 1차 및 2차 모멘트를 유지한다.

또한, 제안된 방법 외에도 고차원 데이터에서 변화점을 탐지하는 기존 검정법 중 두 가지 경쟁 기법을 고려하였다.

• 그래프 기반 방법 (gseg): Chen & Zhang (2015) 및 Chu & Chen (2019)가 제안한 방법으로, R 패키지 gSeg를 사용하여 구현하였다. 그래프는 최소 스패닝 트리를 이용하여 구성하며, 네 가지 에지 개수 스캔 통계를 고려하였다.
  • gseg orig: 원래 방식
  • gseg wei: 가중치 방식
  • gseg gen: 일반화 방식
  • gseg max: 최대값 방식
• 일반화 에너지 거리 기반 방법 (Hddc): Chakraborty & Zhang (2021)이 제안한 방법으로, 기본 거리 메트릭를 이용 거리를 계산한다

 

 

이러한 접근법의 효과를 더욱 분석하기 위해, Chakraborty & Zhang (2021)을 따라 Adjusted Rand Index (ARI)(Morey & Agresti, 1984)를 사용하여 추정된 변화점의 정확도를 측정하였다. ARI는 일반적으로 클러스터링 알고리즘 평가에 사용되지만, 변화점 검정 문제에서도 활용될 수 있다.

변화점 검정에서 ARI가 0에 가까울수록 추정된 변화점과 실제 변화점 간의 차이가 크거나, 실제 변화가 없음에도 변화점을 검출했음을 의미한다. 반면, ARI가 1이면 실제 변화점을 완벽하게 추정했음을 나타낸다. 유의미한 변화점이 검출되지 않은 경우, ARI는 0으로 고정하였다.

 

500회 Monte Carlo 반복 실험을 통해 얻은 실험 결과는 Fig 1의 박스플롯(boxplot)으로 나타내었다. 주요 결과는 다음과 같다.

1. 제안된 방법과 Hddc는 조밀(dense) 및 희소(sparse) 평균 변화 탐지에서 강력한 성능을 보이며, gseg 계열 방법보다 우수하다.
2. gseg 계열 방법은 분포 변화 탐지에서 성능이 저하되며, 반면 Hddc는 조밀 또는 밴디드(banded) 공분산 행렬 변화에서 성능이 저하된다. 이는 Chakraborty & Zhang (2021)의 결과와 일치한다.
3. 제안된 방법의 성능은 선택한 분류기에 따라 달라지며, 특히 높은 차수의 모멘트(moment)나 분포 변화가 발생할 때 차이가 두드러진다.
   • Logis(정규화 로지스틱 회귀): 평균 변화 탐지에서는 우수하나, 다른 설정에서는 검출력이 감소한다.
   • Fnn(완전연결 신경망): 조밀 및 밴디드 공분산 변화 탐지에서 가장 강력한 성능을 보이지만, 다른 설정에서는 성능이 저하된다. 이는 뉴럴 네트워크가 효과적으로 학습하려면 데이터 차원 간 특정한 종속성이 필요하기 때문으로 추정된다.
   • Rf(랜덤 포레스트): 대부분의 설정에서 성능이 매우 안정적이지만, 조밀 공분산 변화에서는 다소 검출력이 감소한다. 그러나 다른 설정에서는 가장 우수한 성능을 보이는 방법 중 하나이다.

 

정리하면 데이터에 대한 사전 정보가 있을 경우, 적절한 분류 알고리즘을 선택하면 제안된 프레임워크가 최적의 성능을 발휘할 수 있고, 사전 정보가 없는 경우, Hddc는 계산량이 지나치게 크기 때문에 Rf(랜덤 포레스트)를 사용하는 것이 가장 실용적인 선택이다. 

 

4.2 Non-Euclidean CIFAR10 Data

 

이 섹션에서는 고차원 비유클리드 데이터에서 제안된 방법의 크기(size) 및 검정력(power) 성능을 분석한다. 특히, CIFAR10 데이터베이스(Krizhevsky et al., 2009)에서 다양한 동물(개, 고양이, 사슴, 말 등)의 인공적으로 생성된 이미지 시퀀스에서 변화점을 탐지한다. 그림 2에서 이에 대한 시각적 예시를 확인할 수 있다.

이를 위해, 머신러닝 분야에서 널리 사용되는 사전 학습된 심층 합성곱 신경망(CNN) 분류기 두 개를 적용하였다.

• vgg16, vgg19:
  • Simonyan & Zisserman (2014)가 제안한 심층 CNN 분류기로, 16~19개의 은닉층과 작은 3×3 합성곱 필터를 사용한다.
  • 일반적으로 사전 학습된 CNN 분류기(vgg16 및 vgg19)를 활용하여 새로운 데이터셋의 이미지를 분류하는 것이 머신러닝 분야에서 널리 사용되는 방법이다.
  • 여기서는 Tensorflow의 사전 학습된 가중치를 활용하였다.

크기(size) 성능 평가를 위해 개(dog)와 말(horse)의 이미지를 각각 1000개씩 랜덤 샘플링하여 두 개의 별도 시퀀스를 생성하였다.

 

대립가설 평가 및 검정력평가를 위해 서로 다른 두 개의 동물 카테고리에서 500개의 이미지를 랜덤 샘플링하여, 다음과 같은 방식으로 배치하였다.

1. 첫 번째 500개 이미지는 한 동물
2. 이후 500개 이미지는 다른 동물

• 고려한 동물 쌍은 다음과 같다.
  • (고양이 → 개, Cat → Dog)
  • (사슴 → 개, Deer → Dog)
  • (개 → 말, Dog → Horse)

실제 변화점은 t0=500에 위치한다.

 

Baseline

• 기존 방법 중, gseg(Chen & Zhang, 2015; Chu & Chen, 2019)만이 이러한 비유클리드 데이터를 처리할 수 있다.
• 따라서, 비교를 위해 gseg 계열의 네 가지 그래프 기반 방법을 함께 사용하였다.
  • gseg orig (기본 방법)
  • gseg wei (가중치 방식)
  • gseg max (최대값 방식)
  • gseg gen (일반화 방식)

 

 

결과는 다음과 같다. 표4의 첫 두 행을 보면 변화점이 존재하지 않을 때, 5% 유의수준에서 경험적 기각률을 나타내고, 이는 모든 방법이 적절한 크기(size)를 유지함을 보여준다. 
표4의 마지막 세 행을 보면 변화점이 존재할 때, 500번 반복 실험에서 평균 ARI(Adjusted Rand Index)를 나타냄을 알 수 있다. 
결과적으로, vgg16 및 vgg19를 활용한 제안된 프레임워크가 모든 경우에서 우수한 성능을 보임
특히, (고양이 → 개) 변화 탐지에서 가장 뛰어난 성능을 발휘하였고,  gseg max 및 gseg gen도 일부 쉬운 경우(사슴 → 개, 개 → 말)에서는 경쟁력 있는 성능을 보였으나, 가장 어려운 경우인 (고양이 → 개에서는 검출력이 감소함을 확인할 수 있다.

5. Real Data application

이 섹션에서는 두 가지 실제 데이터 응용 사례를 제시하고, 제안된 방법의 성능을 4장에서 고려한 다른 방법들과 비교한다. 

5.1 US Stock Market during the Great Recessio

금융 시장에서 변화점을 감지하는 것은 정책 결정자와 투자자에게 매우 중요하다. 본 절에서는 2005년부터 2010년까지 NYSE 및 NASDAQ 주식 데이터를 사용하여 제안된 방법을 적용한다. 우리의 연구는 Chakraborty와 Zhang(2021)의 연구를 기반으로 하며, 해당 연구에서는 "소비자 방어(Consumer Defensive)" 부문에 속한 72개 기업의 주가 변화를 분석했다. 우리는 이를 확장하여 2005년 1월부터 2010년 12월까지 "헬스케어(Healthcare)", "소비자 방어(Consumer Defensive)", "유틸리티(Utilities)" 부문에 속한 289개 기업의 일별 로그 수익률을 포함하는 더 큰 데이터셋을 분석한다. 이러한 부문들은 2007년 12월부터 2009년 6월까지의 "대공황(Great Recession)" 기간 동안 "불황에 강한(Recession-Proof Industries)" 산업으로 식별되었으며, 이 시기 동안 미국 연방정부는 경제 안정을 위한 재정 부양책을 시행했다.

 

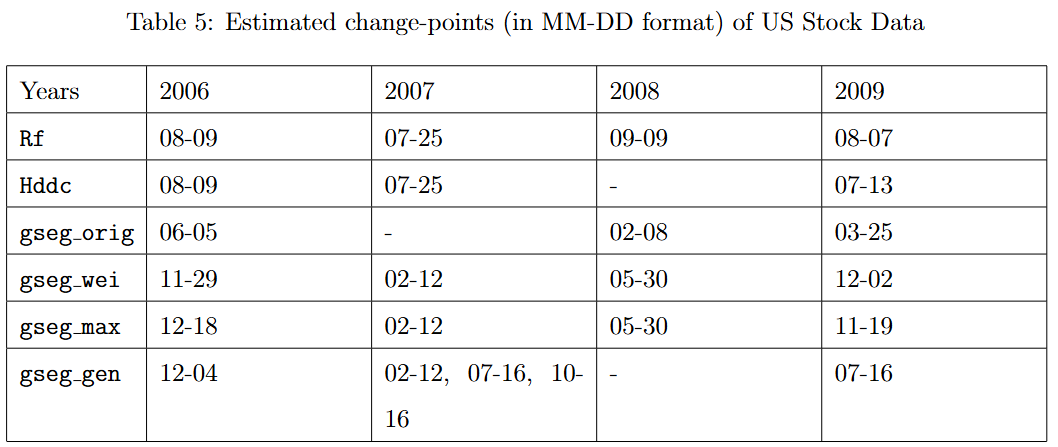
표 5에서는 Rf, Hddc, gseg 유형의 방법을 사용하여 추정된 변화점을 정리하였다. 각 방법은 다중 변화점을 추정하기 위해 Seeded Binary Segmentation(Kovács et al., 2023) 알고리즘에 적용되었다. 표의 결과에서 볼 수 있듯이, 우리가 추정한 변화점들은 경기 침체 기간 동안의 중요한 역사적 사건들과 일치한다. 예를 들어, 2007년 8월 초(07-25-2007로 식별됨)에 시장은 유동성 위기를 경험하였고, 2008년 9월(09-09-2008로 식별됨)에는 "리먼 브라더스(Lehman Brothers)"의 파산으로 인해 국제적인 금융 위기가 발생했다(Wiggins et al., 2014).

Hddc 방법에 의해 감지된 변화점들은 우리의 변화점과 비교적 유사하지만, 2008년의 중요한 변화를 포착하지 못했다. 반면, gseg 방법이 보고한 변화점들은 상당한 차이를 보였다. 주식 가격 데이터의 경우, 일별 로그 수익률의 변화는 평균을 넘어 더 높은 차수(moment)에서 나타나는 경향이 있으므로, 이러한 차이는 gseg 방법이 분포 변화 추정에서 성능이 저하되었기 때문이라고 추정된다(4.1절에서 언급됨).

 

5.2 New York Taxi Trips during the COVID-19 Pandemic

코로나19 팬데믹은 뉴욕주, 특히 2020년 초에 큰 영향을 미쳤다. 뉴욕주, 특히 뉴욕시(NYC)는 바이러스의 진원지(epicenter) 중 하나가 되었으며, 확산을 억제하기 위한 강력한 봉쇄 조치가 시행되었다.

본 연구에서는 코로나19 팬데믹 기간 동안 NYC에서 시행된 여러 봉쇄 조치의 영향을 조사한다.

 

우리는 NYC 택시 및 리무진 위원회(TLC) 여행 기록 데이터베이스†에서 2018년부터 2022년까지의 차량 호출 서비스(FHV) 여행 기록을 수집하였다. 해당 기록에는 승차 및 하차 시간, 하차 위치, 이동 거리 및 기타 중요한 정보가 포함되어 있다. 데이터셋 내의 지리적 정보를 활용하기 위해, 각 하차 지점과 연계된 자치구(borough) 이름을 사용하여 일별 지역 열 지도(areal heat map)를 생성하였다. 이러한 열 지도는 하차 횟수의 공간적 밀도를 시각적으로 나타내며, 이에 대한 예시는 그림 3에서 여섯 개의 열 지도를 통해 확인할 수 있다. Chu와 Chen(2019)은 같은 데이터 소스를 사용하여(다만, 다른 시기와 다른 유형의 택시 데이터를 활용) 30×30 행렬로 요약된 택시 하차 횟수 정보를 분석한 바 있다.

 

표 6에서는 vgg16 분류기 및 gseg 유형 방법(Chu & Chen, 2019에서 설명됨)을 사용하여 추정된 변화점을 제시한다.

특히, 두 방법이 식별한 변화점들은 2021년을 제외하면 서로 밀접하게 일치한다. 이러한 주요 변화들은 2019년 북미 한파(2019-01-31), 여름 방학의 잠재적 영향(2019-08-31), 그리고 NYC의 첫 번째 봉쇄 조치 시행(2020-03-17)과 같은 사건과 관련이 있다.

 

예를 들어, 그림 3a와 3b는 각각 한파 발생 전(2019년 1월 15일)과 한파 발생 후(2019년 2월 15일)의 지역 열 지도를 나타내며, 택시 이용량의 현저한 감소를 보여준다. 이후, 그림 3c와 3d의 지역 열 지도는 여름 방학 종료 이후 택시 이용량이 증가하는 영향을 보여준다. 또한, 그림 3e와 3f는 봉쇄 조치 전(2020년 3월 5일)과 봉쇄 조치 후(2020년 4월 5일)의 지역 열 지도를 각각 나타내며, 택시 이용량의 급격한 감소를 보여준다.

6 Discussion

본 논문에서는 분류기(classifier)를 기반으로 한 새로운 오프라인 변화점 탐지(offine change-point detection) 프레임워크를 제안한다. 변화점 탐지에 관한 방대한 문헌이 존재하지만, 본 연구의 접근 방식은 네 가지 주요 측면에서 차별성을 갖는다.

첫째, 본 방법은 완전히 비모수적(nonparametric)으로, 데이터 분포나 분포 변화의 구조에 대한 어떠한 모수적 가정도 필요로 하지 않는다.
둘째, 현대적인 분류기의 성능을 활용함으로써, 제안된 프레임워크는 다양한 차원과 유형의 데이터에 폭넓게 적용될 수 있다.
셋째, 적절한 분류기를 선택함으로써 사전 정보를 통합할 수 있어 검정력(test power)을 향상시킬 수 있다.
넷째, 적절한 샘플 분할(sample splitting) 및 절단(trimming)을 수행하면, 검정 통계량(test statistic)은 특정 분류기의 선택과 무관하게 극한적으로 중심적인 가우시안 과정(Gaussian process)의 최댓값(supremum)으로 수렴하며, 이를 통해 구현이 용이해진다.

본 연구를 마무리하며, 향후 탐색할 만한 몇 가지 연구 방향을 제시한다.
첫째, 5장에서 다룬 실데이터 분석(real data analysis)은 시계열 데이터 간의 시간적 의존성(temporal dependence)을 포함할 가능성이 있다. 따라서, 제안된 방법을 약한 종속성을 갖는 시계열(weakly dependent time series)에 적용할 수 있도록 확장하는 것은 흥미로운 연구 주제가 될 것이다.
둘째, Londschien et al.(2023)의 연구에서 영감을 받아 계산 복잡도를 줄이는 것이 가능할 수도 있다. 모든 잠재적 변화점에 대해 AUC(Area Under Curve)를 계산하는 대신, 데이터 시퀀스의 사분위수(quartiles) 등 초기 지점에서 AUC를 계산한 후, 가장 높은 AUC 값을 갖는 후보 변화점 주변에서 세밀한 탐색을 수행하는 방식이 고려될 수 있다. 그러나 이러한 2단계 접근법의 이론적 성질을 분석하는 것은 도전적인 과제가 될 것이다.
셋째, 현재 설정은 비지도 학습(unsupervised learning) 환경에서 진행되었으며, 이에 따라 특정 샘플 분할 및 절단이 필요하다. 따라서, Li et al.(2024)에서 다룬 바와 같이, 지도 학습(supervised learning) 환경에서 검정 통계량의 점근적 성질(asymptotic properties)을 연구하는 것도 흥미로운 연구 주제가 될 것이다.