[Quantative Finance 2020]Index tracking through deep latent representation learning(Kim&Kim)

https://doi.org/10.1080/14697688.2019.1683599

 

본 논문에서는 Index tracking을 위해 Stack AutoEncoder를 이용하여 벤치마크지수의 추즉오류를 최소화한다. S&P 500, FTSE 100 및 HSI index에 방법론을 적용한다. 

인덱스 펀드를 만들거나 할 때 보통 인덱스를 구성하는 모든 종목을 가지고 구성하게 되면, rebalancing 시 큰 Transaction cost나 complexity 우려가 있다. 그렇기에 종목을 구성하는 일부 종목을 가지고 가중치를 조절하여 해당 index를 잘 tracking 하는 portfolio를 만드는 것이 Index Tracking이 목표이다.

기존에는 주로 optimization approach를 중심으로 연구가 진행되었지만, 최근에는 ML 기반의 차원 축소 기법이나 클러스터링 방법론들도 제안되고 있다.

이 논문은 최근에 autoencoder의 reconstruction loss가 작은 종목들을 골라서 아주 단순한 weighting scheme만 사용해도 웬만큼 index tracking이 된다는 연구의 extension으로 가진다. 

Index Tracking

Index tracking은 특정 시장 지수의 성과를 최대한 가깝게 복제하는 것을 목표로 한다. 시장 지수는 일반적으로 기초시장 자산 가치 중 선택된 집합의 시가 총액의 가중합으로 시장을 표현한다. 가장 잘 알려진 지수는 S&P 500이 존재하고, 한국에서는 코스피 200 등의 지수가 존재한다. 이러한 시장지수는 다양한 포트폴리오는 투자 전략의 지표로서 사용되며, 이를 장기적으로 초과하는 것은 매우 어려운 과제로 알려져있다. 이런 이류로 시장지수를 추적하는 인덱스 펀드는 주목받는 투자 수단 중 하나이다. 인덱스 펀드의 장점은 Dorocakova (2017)에서 광범위하게 작성되어있으며 2015년 기준 미국의 인덱스 펀드에만 약 2조 달러가 투자되었다(Strub and Baumann 2018)

 

시장 지수와 인덱스 펀드 간의 성과차이를 추적오차(tarcking error)라고 한다. 

물론 시장 지수의 모든 구성 요소를 시가 총액의 비율에 따라 매수하면 추적 오차가 0인 시장지수를 복제할 수 있다. 이를 Full-replication, 완전 복제라고 한다. 하지만 이 방법은 현실적으로 구현하기 매우 힘들다. 

예를 들어, S&P 500의 경우 2000년에 구성 요소가 60번 변경되었고(Beasley et al. 2003), 1995년과 2000년 사이에는 235번 변경되었다(Blume and Edelen 2002). 이런 시자으이 변화에 따라 거래비용의 증가와 인덱스 펀드의 수익률 감소로 이어진다. 또한 완벽한 포트폴리오 구성을 위해서는 충분한 자금이 필요하고, 유동성이 적은 자산 구매 시 매수-매도 스프레드의 큰 차이는 비용을 더욱 증가시킬 것이다. 

 

Partial replication, 부분복제는 이런 완전 복제보다 구현 가능한 방법이다. 시장 지수를 근사화 하되, 더욱 더 적은 종목을 이용해 구성하는 것을 목표로 삼는다. 얼마나 근사화 할것인지는 포트폴리오의 목적에 따라 달라 질 수 있다. 

다만, 부분복제의 경우 자산의 최대 개수를 지정하는 제약 조건, Cardinality constraint가 포함되기에 최적식을 구하는 것이 NP-hard 문제 중 하나인  Mixed Integer Qudaratic Programming 문제가 된다. 

이를 해결하기 위해 다양한 연구가 진행되어왔다. 

 

Index Tracking의 기존 방법론

Optimal index Tracking:

휴리스틱 알고리즘을 이용한 Cardianrity cosntrained portfolio:Chang et al. (2000)

Factor 기반 Index tracking(linear function of factors: Famma and french): Corielli and Marcellino (2006)

IP 기반&유사도 최대화 방법: Robust portfolio selection for index tracking

 

제약조건 추가하기 

리밸런싱, 거래비용 추가: Beasley et al. (2003), 

거래비용 상한을 포함하는 최적 샘플링 방법: Montfort et al. (2008)

Tacking error와 거래비용 간의 최적점: Strub과 Baumann (2018)

 

다양한 ML 알고리즘 적용

유전 알고리즘 기반: Oh et al. (2005)

SVM Regression 기반 저변동성 포트폴리오 구성: Volatility forecasting for low-volatility portfolio selection in the US and the Korean equity

Mahalanobis disatnce를 이용한 SVM??

 

딥러닝을 이용한 Index tracking:

Heaton(2016) Deep Learning in Finance

Ouyang et al. (2019): HSI 지수에 동적 가중치 계산방법 적용

(autoencdoer를 사용해서 본 논문과 매우 비슷한 접근법으로 보임, 다만 지수를 직접 Auto Encoder에 사용하지 않고 Auto Encoder를 통해 각 주식의 Reconstruction error를 이용, Reconstruction error가 적을 수록 시장 포트폴리오와 더 만은 공통 정보를 공유한다고 간주함, 이후 DNN을 통해 선택한 주식의 가중치를 결정)

 

본 논문은 특히 Ouyang et al. (2019) 과 AutoEncoder를 사용한다는 점에서 비슷하지만, 기존 논문의 경우 지수의 수치가 오토인코더의 학습과정에서 아무런 역할을 하지 않는다는 것이 문제이다. 또한 아키텣쳐가 완전히 계층적이지 않아 학습이 적절히 이루어졌다고 보기 어렵다. 

본 논문에서는 시장 지수를 대리하는 deep latent representation을 가지는 심층 오토인코더를 구성함으로서 이러한 문제를 해결하며,33% 이상의 개선을 보인다. 

 

BackGround 

Return of index on day t

Rt 즉, Index의 tth day의 수익률은 다음과 같이 정의되며, W는 weight of asset a on day t, I은 Index poll안에 있는 asset의 집합, r은 return of assent a on day t이다. 

또한 식 (2)에 따라 가중치는 음수가 될 수 없으며(공매도는 고려하지 않는다), 그 총합은 1이다. 

Problem formulation

Index Trackinng은 기본적으로 인덱스와 Tracking portfolio의 차이를 최소화 하는 것이다. 즉, Cardinarity제약(k개의 asset을 선택) 하에서 적절한 가중치를 선택하여 두 수익률이 밀접하게 움직일 수 있도록 하는 것이 목적이다. 

이러한 밀접성을 측정하는 기준은 여러가지가 있지만, Monfort(2008)에서와 같이 일반적으로 MSE loss를 선택하였다. 

가장 직접적으로 문제를 해결하는 방법은 index 구성 비중이 가장 큰 자산을 선택하는 것이다. 그러나 일부 경우 인덱스의 구성이 알려져 있지 않거나 투자할 수 없는 경우가 있다. 예를 들어 Spot Energy Index는 거래소에서 거래되지 않는 구성 요소를 포함하고 있다(Andriosopoulos와 Nomikos 2014). 이러한 경우에도 본 방법은 index tracking이 가능하게 한다. 

 

Model for Index tracking 

Asset Selection using deep autoencoder

가장 관련성이 높은 자산을 구축하기 위해 DNN을 구성하는 것은 하나의 문제해결 접근법이 될 수 있다. 이를 위해 AutoEncoder 혹은 Deep  AutoEncoder가 사용될 수 있다. 다시 말해 오토 인코더를 통해 input x와 output x'이 가장 유사할 수 있게 학습시킨다. 이를 통해 모델이 잠재벡터로 특성을 잘 추출할 수 있게 한다. 

AutoEncoder는 Input의 representiveness를 잘 보존함으로 인덱스 추적을 위한 관련성이 높은 자산을 식별하는데 사용되어왔다. 다만, 그 세부적인 구조에 관해서는 논문에 따라 달라져왔다. 

 

그림을 보면 각 Xi들은 T일 동안의 일별 수익률 벡터로, 각각의 자산을 의미한다. Heaton 등(2016)과 Ouyang 등(2019)에서는 이들의 mse of reconstruction이 작은 K개의 value를 골라 Tracking portofolio로 구성하였다. 이러한 자산들이 더 높은 공통 정보를 가지고 있다고 주장했기 때문이다(공통된 정보가 많다는 것은 market을 잘 대표한다고 볼 수 있다, 다만, 논문들에서는 공통적으로 높은 d를 가지는(낮은 reconstruction error) asset과 반대로 가장 비공통된 asset을 합해 포트폴리오를 구성한다..? 이 부분이 이해가 잘 되지 않는다)

Heaton(2016)에서는 이 들에 동일한 가중치를 부여하였고, Ouyang(2019)에서는 가중치 계산을 위해 DNN을 추가로 활용했다. 허나 후자의 방법은 일부 자산을 공매도 가능한 w가 음의 가중치를 생성했기에 전통적 구현에 부합하지 않는다. 다만, 좋은 tracking score를 보여주었기에 본 논문에서 관련한 접근법을 채택하였다. 

 

Deep Auto Encoder(which paper proposed)

본 논문에서는 3-hidden layer를 가지는 deep autoencoder를 이용하는데 이는 기존의 Ouyang et al. (2019)에서 따온것이다.  이때 y는 전체 asseto의 0.25의 크기를 z는 0,0625의 크기를 가진다. 이는 임의로 설정된 것으로 너무 급격하게 정보 축소가 이루어지지지 않도록 설계되었다. 또한 비선형성을 충분히 반영하기 위해 tangent hyper를 활성화 함수로 사용하였다. 이는 -1,1사이의 값이 존재하는 return을 표현하기에 적합하기에로 보인다.

loss는 reconstruction error를 최소화하는(x와 x'를 최대한 유사하게 만드는) 것을 목표로한다. 추가적으로 regularization term으로 overfitting을 방지하는 것도 가능하다. 실제로 이전 논문인 Ouyang et al(2019)에서는 가중치에 관한 regularization term을 추가하였다.

하지만 본 방법에서는 reconstruction 전(decoder를 통과하기 전) single node로 압축하기에 overffing은 큰 문제가 아니라고 한다(추가적으로 실험 진행시 큰 효과가 없음을 확인/사실 논문에서 이유로 제시한 것이 잘 이해가 안된다..ㅜ)

 

w는 Capital Asset model에서 martket factor와 유사한 역할을 한다, 각 자산의 가격의 선형조합이 market의 value을 표현가능하다고 명시한다. 즉, 단일 노드 w는 시장지수로 해석 가능함으로 이를 이용하여 w와 자산의 수익벡터 xi와의 유사성이 큰 K개 중 가장 큰 자산을 선택한다. 

CAPM, 출처: wiki

시장 지수를 산출하는 방법은 각 주가 지수 별로 다르다. 수정주가평균, 시가총액 가중 법, 등액 가중 등이 존재한다. 수장주가 평균은 시장을 대표하는 업종 대표주를 모아 그 주식들의 현재가를 총 종목의 수로 나눈다(다우 지수나 닛케이 지수 등이 존재, 다만 현재는 대다수 시가총액 가중법을 이용). 시가총액 가중법을 이용한 지수 산출은 나스닥, S&p 500 등 다양한 시장에서 이를 사용한다. 산출법은 기준시점의 시가총액과 현재시점의 시가총액을 비교하여 그 배율에 따른 주가지수를 산출한다. 이들은 다만, 시가충액이 큰 대형종목에 주가지수가 큰 영향을 받는다. 
추가적으로 Market portfolio 또한, 시장에서 거래되는 모든 종목의 증권을 각각의 시가총액비율로 조합한 포트폴리오라고 한다(시가총액 가중법과 비슷)
다만, 본 논문 및 기타 다른 Index tracking 논문들에서는 대다수 AutoEncoder 이용 시 종목을 1:1:1로 두고 잠재벡터를 구하고 있기에 이에 따른 변형이 필요하지 않나..고 생각이 든다(개인 생각)

추가적으로 latent vector로 w를 구한다고 해도 실제 그것이 전체 시장을 대표한다고 할 수 있을까..?
w를 차라리 목표하는 Index(market)을 쓰고 이를 이용해서 reconstruction error를 구할때(decoder만 엄청 늘려서) 해당 error가 적은 자산들을 고르는 방법도 생각해볼 수 있을듯

 

유사성을 측정하는 도구로 입증된 것 중 Kim and Kim (2018)의 상관계수(7)와 mutual information, I(xi; ω)(8)(Kingma and Welling 2014)을 사용한다. 그 각각의 수식은 다음과 같다. 

(8)식을 조금 더 설명하면 p는 x와 w의 joint proabiltiy distribution을 의미한다. 

 

여기서 이전 발표 연구 (Heaton et al., 2016; Ouyang et al., 2019)와의 차이가 존재한다. 이전에는 reconstruction error만을 고려한 이후 다른 방법으로 가중치를 사용하였다(w 고려안함), 그러나 본 연구에서는 이를 (7), (8)을 이용해 고려하였다. 

Stacked autoencoder

추가적으로 같은 아키텍쳐 레이아웃을 지니고 있지만(그림2, Deep AE)  훈련방법에서 차이를 둔 것이 Stacked AutoEncoder이다(보다 특징을 잘 추출하기 위해). 

학습법은 위의 Algorithm 2를 보면 알 수 있듯이, W1과 W1'을 우선 학습하고, 이에 따라 x와 x'(output)의 loss를 minmize하게 학습한다. 이후 W2, W2'은 이전 layer의 input가 output의 reconstruction loss가 적게 하는 방향으로 학습이 이루어진다. 즉, 각각의 layer를 순차적으로 학습하고 최적화한다. 이는 reprensentation learning에 더 효과적이라고 알려져있다. 

이런 Stacked autoencoder를 사용한것이 이 논문의 주 기여 중 하나이다. 

 

weight selection 

k개의 자산을 선택한 이후 포트폴리오를 구성하기 위해서는 각 자산에 가중치를 부여해야한다. 동일 가중치방식을 사용할 수도 있고, 음수 가중치 등을 설정하는것도 가능하다. Chen&Kwon(2012)에 따르면 수익의 상관관계를 사용하나 가중치가 있다. 

본 논문에서는 이에 기반하여 자산 a와 다른 모든 자산의 집합 b의 상관관계의 지수합을 이용해 수식을 설정하였다.

혹은 상관이 약한 자산에 더 많은 가중치를 부여하는 방법도 가능하다. 

이는 위 식의 역이 될 것이다. 

이때 두 식 모두에서 k는 가중치의 총 합이 1이 되도록하는 정규화 상수이다. 

 

혹은 이외에도 자산이 선택된 이후 방정식 3(아래의 첨부)의 목적함수를 최적화하는 방향으로 가중치를 계산했다. 이는 자산이 선택되어있을 때는 풀 수 있는 최적화 문제(quadaratic program)가 된다. 

 

다만, 본 논문에서 이 3가지 가중치와 동일 가중치 방식을 모두 사용해본 결과 특정 가중치 방식이 우수하지 않았고, 특히 (3)을 이용해 가중치를 최적화한 경우 오히려 더 좋지 않은 성능을 보여주었다. 이는 과적합에 의한 것으로 유추된다. 

따라서 본 논문에서는 모두 동일 가중치 방식만을 사용하여 결과를 도출한다. 

 

Experiment(performance test)

실험은 아래의 6개 모델에 관해서 진행되었다. 

(a) 3-Layer Autoencoder (b) CC-3-Layer Autoencoder (c) MI-3-Layer Autoencoder (d) Stacked Autoencoder (e) CC-Stacked Autoencoder (f) MI-Stacked Autoencoder

이때 CC는 위에서 말한 상관계수를 이용한 방식이고 MI는 mutual information을 이용해 자산을 고른 것을 말한다. 

 

데이터는 미국의 S&P 500, 영국의 FTSE 100, 홍콩의 HSI를 이용했고 test는 2017 11월 1일~2018 10월 31일까지, train은 2015 11월 1일 부터 2017년 10월 31일까지 직전 2년을 사용했다. 추가적으로 분기별 rebalancing cost를 0.2%로 잡았으나 적용한 결과가 적용하지 않았을 때와 비교하여 큰 차이가 없기에 이를 제거하였다. 

 

Tracking error 확인을 위해 RMSE와 tracking error volatility (TEV)를 지표로 확인했다(아래의 수식의 각 파트이다)

k의 개수, 즉, 자산의 수는 1,2,3 각각 3가지 기준에 관해 진행되었다. K1 = 0.05∗|I|, K2 =0.1∗|I|, K3 = 0.2∗|I|, 로 전체 자산의 개수의 5%, 10%, 20%이다(FTSE와 HSI에서는 0.1, 0.2, 0.3으로 변형하였다)

결과는 아래와 같다. 

 

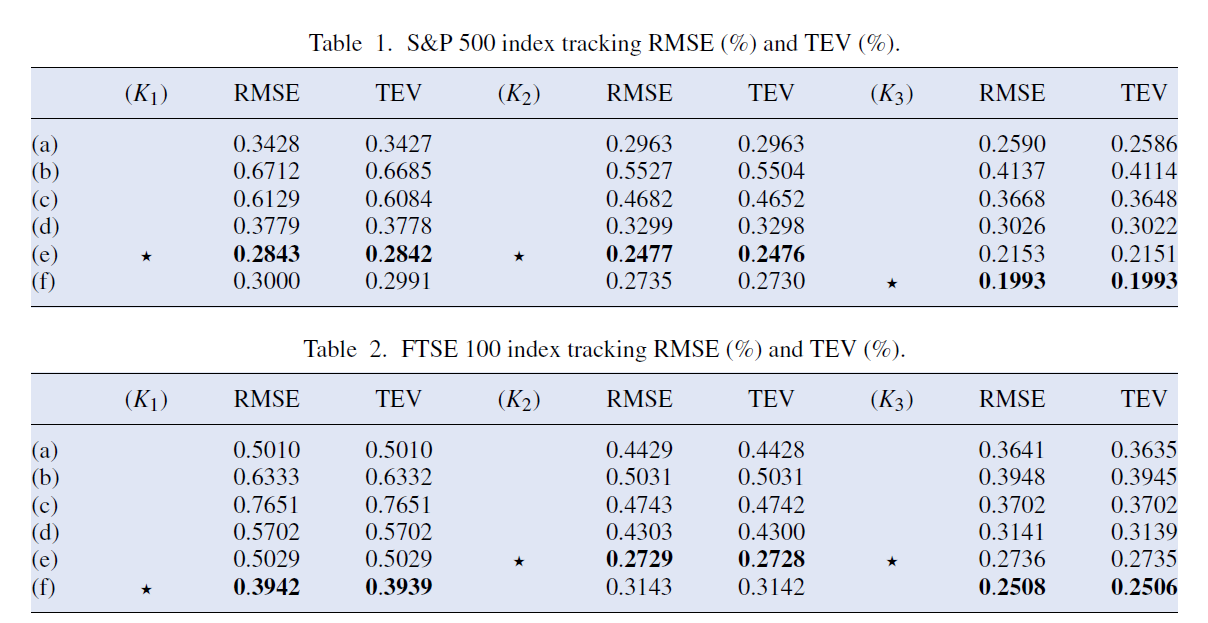
표 1~3은 전략 (b)와 (c)가 전략 (a)의 성능을 개선하는지 여부는 결론을 내리기 어렵지만, 전략 (e)와 (f)는 명확하게 전략 (d)의 성능을 개선함을 보인다(stack Auto Encoder의 유용성 확인). 또한, 표는 추적 포트폴리오에 더 많은 주식이 포함될수록 직관적으로 추적 오차가 낮아진다는 것을 보여준다. 

subsection으로 cumlative return을 보여지만 생략하였다. 

 

Conclusion 

Stacked Auto Encoder가 기존의 AE를 사용한 방법보다 좋은 성능을 보여줌을 보여주었다. 더욱이 자산의 수익벡터와 w간의 통계적 정의가 자산 선택 기준에 있어서 Reconstruction error를 사용한 방법보다 우수함을 보여준다. 

참고자료

Auto Encoder 및 Stacked AutoEncoder

 

https://deepinsight.tistory.com/126

[정리노트] [AutoEncoder의 모든것] Chap3. AutoEncoder란 무엇인가(feat. 자세히 알아보자)

추가 의문 

AE를 통해 latent vector를 구한뒤 그것과 자산 i와의 상관을 확인하는 것은 무슨 의의가 있는가..?

아직 이 부분이 의문이다