[DFL] Decision-Focused Learning: Through the Lens of Learning to Rank( ICML 2022, Mandi et al.)

Decision Focused learning 문제를 해결하기 위해 다양한 접근법이 도출되는 것 같다. 대다수 accpet된 논문들의 경우 loss function이나 방법론을 정말 획기적..? 혹은 다른 필드에서 쓰이는 방법들을 잘 변형해서 적용하는데, 이정돈 해야 탑티어 논문인가...? 싶기도 하다. 

이번 논문은 LTR에서 사용되던 방법을 이용해서 DFL문제를 풀겠다는 요지의 논문이다. 간단히 요약하면 

1. Feasible solution들의 집합 v를 S라는 부분집합을 통해 대체한다(S는 기존의 F.S와 확률적으로 추가된다) - 선행논문 중 하나인 Mumba et.al 방법론 

2. objective function을 통해 S를 정렬하고, 이를 실제값을 이용한 정렬된 S와 비교해 ranking loss를 구한다. 

-논문에서 제시하는 방법론 

3. 구한 loss를 통해 예측모델을 업데이트한다 

https://icml.cc/virtual/2022/spotlight/18376

ICML 2022 Decision-Focused Learning: Through the Lens of Learning to Rank Spotlight

 

https://github.com/JayMan91/ltr-predopt

GitHub - JayMan91/ltr-predopt

 

Abstract

Based on a recent work that proposed a noise contrastive estimation loss over a subset of the solution space we observe that decision-focused learning can more generally be seen as a learningto-rank problem, where the goal is to learn an objective function that ranks the feasible points correctly. 

 

최근 방법론 중 subset of solution space의 loss로 문제를 접근한 것을 보고( Mulamba, M., Mandi, J., Diligenti, M., Lombardi, M., Bucarey, V., and Guns, T. Contrastive losses and solution caching for predict-and-optimize) 이를 이용해서 feasible points의 순위를 매기는 목적함수를 학습하는 것으로 문제를 바꾸었다. 해의 하위 집합이 주어진 경우 point별, pair별, list별 랭킹 손실 함수를 만들었다. 

Introduction

Predict & Optimize 방법론의 개요와 문제를 설명하고 최근 DFL의 방법론들을 설명하고, Abstract에서 밝힌 것처럼 noise-contrastive estimation을 이용한 Contrastive losses and solution caching for predict-and-optimize(Mulamba et al. (2021)의 접근법을 설명한다. 이 방법은 non-optmal feasible soultion을 negative sample[최적해가 아닌 feasible solution]로 고려하는 Surrogate loss를 제안하고, 이를 통해 True optimal과 negative example의 거리를 최대화 하는(표현상으로는 차이를 극대화 하는) 손실함수를 제안했다. 우리는 DFL이 일반적으로 LTR, Learning to rank의 접근법으로 볼 수 있다고 주장합니다. LTR에서는 각 쿼리에 대해 항목의 목록과 해당 항목의 특성 변수가 주어집니다, 학습 목표는 각 쿼리에 대해 상위 항목의 순위를 올바르게 매길 랭킹 함수를 학습하는 것입니다(즉, 답 자체를 맞추는 것이 아니라 순위를 잘 맞추는, top k? 정답에 가까운 답을 내게 만든다)

 

Constraint optimization 관점에서 보면, Feasible solution을 부분 정렬(partial ordering)하는 것은 목적함수에 의해 결정된다. LTR과 비교하면, 크게 2 차이가 있다. 

1. 목적함수의 구조 자체는 이미 주어져 있으며, 일부의 파라미터는 추정되어야한다(목적함수의 형태가 주어져있다는 뜻인듯)

2. 모든 CO query에 관해(instance) Item의 집합은 Feasible solution의 집합과 같다. 단, 모두 열거하는 것은 불가하다. 

1의 경우 목적함수가 미분가능하다면, 문제되지 않으며, 2의 경우 Mumba et.al에서 제시한 것과 같이 부분집합을 통해 해결가능하다. 

 

논문에서는 DFL을 Ranking 문제로 치환해서 접근하였다는 점, 여러 대표적인 ranking방법들을 비교하였다는(pointwise, pairwise, listwise를 이용) 점과 pairwise ranking이 Mumba et al(2021)의 일반화된 수식임을 보인다. 마지막으로 linear objective function인 경우 MSE와 regret of prediction(task의 평가)의 절충식으로 pointwise와 pairwise 수식이 표현됨을 보인다. 

 

Problem Statement and Motivation

Discrete Combinatorial optimization 문제를 고려한다. 

이때 V는 k차원의 정수 집합의 부분집합으로 feasible integer solution의 부분집합이다(제약조건으로 결정된다). 

f는 V*C로 결정되는 objective function으로 C는 domain of the vector of parameter c(실수의 부분집합)이며 unknown parameter이나, Historic dataset, D = {xi, ci}로 추정된다. 이를 이용해서 supervised model m(w,x)를 학습하고 c를 예측한다. 

Optimal solution of (1)은 v*(c)로 표현한다. 

 

전통적인 접근법으로는(Task driven) c와 c^의 difference를 줄이는 것을 목표로 했다. 예를 들어, regression 문제에서 multi-output mse를 줄였다. 

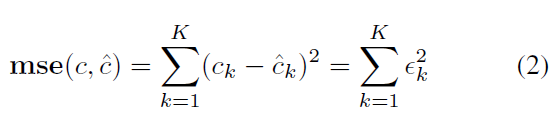
반면, DFL은 c의 경우는 intermediate result(중간 결과이다)이다. Final output은 바로 최적화 문제의 해인 v*(c^)이다. 

DFL의 목표는 real cost vector(unknown vector)가 있을 때, downstream optimization(실제 해결하고자 목적문제, ex: 포트폴리오 최적화에서, 예측 단계: 주식의 미래 수익률을 예측합니다. Downstream optimization: 예측된 수익률을 바탕으로 최적의 포트폴리오 구성을 결정)에서 해결 해결책 v*(c^)의 영향을 최소화하는 것이다. c^의 성능을 측정하기 위해 조합 최적화의 Regret을 계산한다. 이는 최적 목적값 f(v*(c), c)와 f(v*(c), c)의 차이로 나온다. 

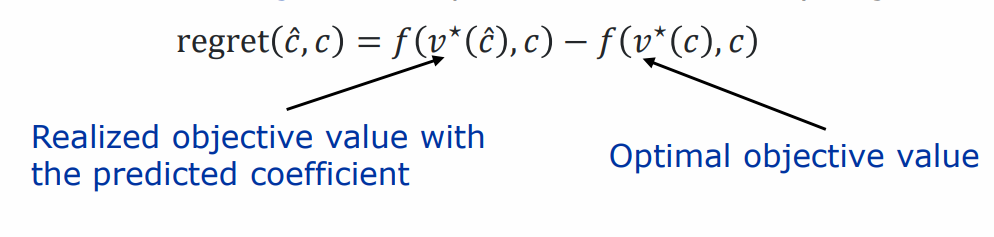
이상적으로, c를 잘 예측하는 모델의 파라미터 w가 regret loss를 최고화 하는 것을 목표로 한다 이를 위해 regret loss를 역전파해야하며, 정확한 derivate를 계산해야함을 의미한다. 문제는 이때 V가 discrete하고 non-continuous 함으로 문제가 된다. 

 

여러 최근 연구들이 이를 다루며, gradient를 계산하기 위해 학습 과정 중 최적화 수식 (1)을 반복적으로 풀어야한다. 따라서 확장성이 연구의 주요과제 중 하나이다. 

기존 연구들은 backpropagation through combinational solver을 거쳐야했기에 매우 time consume이 길었다

Contrastive Surrogate loss - Mulamba et al 

Mulamba et al(2021)을 읽고 더 보충하겠다. 내용 이해가 안되는 부분이 아직 많음

앞서 언급한 Mulamba et al(2021)에서는 이를 위해 Alternative class of loss function을 제안하며 이는 아래와 같다. 

이때 v는 feasible solution을 의미하며 수식을 보면 알 수 있듯이 위의 식은 softmax의 변형이다. (1)을 minimize한다면 (4)는 maximixe하는 v일 것이다(수식에 - 붙음). S, subset of feasible set를 알 수 있다고 가정한다면, S\{v*(c)}는 negative sample로 가정한다(?)(optimal solution이 아닌 해를 negative solution이라고 하는듯). 이러한 가정 아래에 아래의 noise contrasive estimation loss를 정의한다. 

이를 통해 식 (5)는 미분가능하며, 미분과정이 식 (1)의 최적화 문제를 해결하는 과정을 포함하지 않는다는 것에 주요하다(?). 

또한 S의 해들이 임의의 비용 벡터의 최적해인 경우, 이는 V(feasible set)의 convex-hull에서 훈련하는 것과 동일하다. 

NCE loss란?
Self-supervised learning의 Constrastive loss에서 나오는 loss함수(논문 : A Simple Framework for Contrastive Learning of Visual Representations, SimCLR)이다. 
기준 acnhor와 positivie 사이는 유사해지도록 하고, negative한 경우는 멀어지도록하는 loss이다. 이전 선행 논문인 Mumba et al(2021)에서는 v*을 제외한 나머지 S를 negative sample로 정의하고 NCE loss를 사용하여 문제를 풀었다. 
https://www.blossominkyung.com/deeplearning/contrastive-learning 추가참조

Rank Based Loss Functions 

Rank based loss function에 관한 자세한 내용은 블로그의 다른 글에서 LTR을 설명하며 간단히 정리했다. 하단의 링크 참조 

 

Partial ordering for v(element of feasible set)에 관해 우리가 만일 real value c(given c)를 안다면

Ranking은 좌측과 같을 것이다.

그러면 학습의 목표는 결국 predictied value c^에 관해서(우측)도 위의 given c가 주어졌을 때의  ranking이  잘 유지할 수 있도록 하는 것이 핵심이다. 즉, c에 따라서 v의 ranking을 잘 학습하는 것이 목적이다

 

LTR과 비교해서 결국 historical data x가 query이고, V(set of feasible solution)이 item이다. 

단, own set of feature varible이 존재하지 않고, 동시에 ranking function이 decision making의 objective function(간단히 말해 1등, 2등, 3등의 ranking fucntion에서 100점, 80 점 등으로 objective function의 값으로 바뀜)으로 바뀐 점, 가장 마지막으로 모든 v에 관해 ranking을 적용하는 것은 불가능하기에 부분집합 S를 만들어 이를 극복하고자 한다. S에 관한 알고리즘은 Algorithm 1에 공개되어있다. 

How to make subset of feasible solution S?

알고리즘 1을 보면 결국 S는 

1. 주어진 x로부터 나온 historical c를 통해 나오는 feasible solution v를 S로 할당

2. 하이퍼파리미터 p_solve를 통해 문제를 얼마나 확률적으로 풀지 결정, 만일 p_solve가 0.3이라면 구해진 c에 관해 30%확률로 문제를 푼다. 

3. 문제를 푼 경우 구한 최적의 v를 S에 추가하고 Loss를 추가하고 예측 모델 w를 L을 이용 update한다. 단 이때의 L은 ranking loss의 loss(현재의 S를 이용해서 계산)

로 이루어진다. 

(논문에서 말하길 이 방법은 선행 논문인 Mumba et al  2021에서 나온 방법이라고 한다)

이제 이후의 ranking 알고리즘은 주어진 S에 관해 어떻게 ranking을 매길지 정한다. 

 

Pointwise Ranking

Pointwise는 직관적으로 말해 ranking과 item 간의 1대1 관계를 찾는 방법이다. 따라서 주어진 S에 관해 다음과 같이 학습이 이루어진다.

objective function f의 차이(LTR에서는 두 ranking score의 차이)를 계산한다. 

f(v,c^)의 차이면 결국 그냥 regret minimize랑 동일하지 않나...? 

 

- Pointwise의 직관적 idea

이를 직관적으로 objective function이 linear하다고 해보자. 즉, f(v,c) = cTv라고 하자. 그럴 경우 수식은 다음과 같이 변경되며, 1차 미분된 식도 구할 수 있다. 

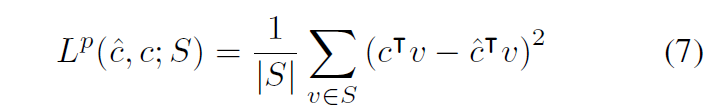
만일 문제를 combinational problem이라고 하면, v는 0,1의 값을 가지며, 이때 0인 경우 gradient에 관여하지 않으며, 또한 (8)의 v의 계수는 두 object value의 차로 결정됨을 알 수 있다. 

 

- pointwise loss as a regularizer 

또한 식을 아래와 같이 변형 가능한데, 이때 입실론 i는 unkwon c의 predicted error이고(2) r은 아래와 같이 정의된다. 

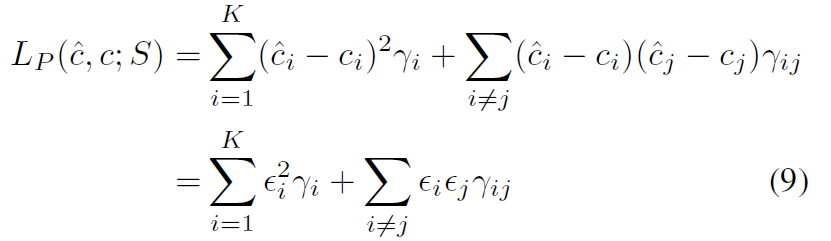
이 경우 이는 MSE의 가중치가 추가된 형식으로 생각가능하다. 

추가적으로 V가 만일 combinational problem, 즉 {0,1}인 경우 ri은 vi가 얼마나 value 1을 가지는지에 관한 빈도를 의미하게 된다. 또 r_ij는 vi와 vj가 동시에 1을 가질 빈도를 의미한다. 만일 S=V라면 식은 다음과 같이 변형되고 이는 mse loss에 regularizer가 추가된 버전으로 해석가능하며, 이는 후보군 c 간의 crossed error를 penalized한다. 

Pairwise Ranking

pairwise의 경우 두 i,j의 순서를 고려하는 것이다. 예시가 매우 적절하다 생각해서 간단히 옮겨 보았다. 

- example & motivation

V = [0; 0]; [0; 1]; [1; 0]; [1; 1] 이라고 할 때 real c = [2,-5]라고 하고, objective function은 min을 목적으로 한다 하자. 

그러면 c에 관해 v*는 [0,1]이다(각 objective value가 0,-5, 2,-3 이된다 그럼으로 제일 작은 0,1)

이때 우리가 c1과 c2로 각각 c에 관한 예측값을 구했을때, c1은 [-1,1], c2 =[5,11]이라고 하자. 

그러면 아래와 같다. 

feaible set V	real C: (2,-5)	c1: (-1,1)	c2: (5,11)
[0,0]	0	0	0
[0,1]	-5	1	-11
[1,0]	2	-1	5
[1,1]	-3	0	-6

 

그럼 point wise loss로 따지면 

c1의 경우: 54 = (0+(-5-1)^2 +(2+1)^2 +(-3-0)^2) c2의 경우: 54 = (0 + (-5 + 11)^2 + (2 - 5)^2 + (-3 + 6)^2).

이 경우 point wise loss는 둘다 54(둘의 f의 값 비교)로 동일하지만, v*을 각각 보면 [1,0], [0,1]로 regret은 다르다. 그럼으로  pair wise가 필요하다

의문: point wise에서도 ranking을 직접 이용하면 되지 않나...?, 1순위 2순위 등으로 매겨서 -> 어차피 그게 listwise랑 동일 해결!

 

Pairwise ranking using margin(Joachims, 2022) - (11)

ordered pair (p,q)에 관하여, (p,q)는 모든 S에 관한 ordered pair이다. 이때  $OP_c^S$를 아래와 같이 정의한다(즉, p가 q보다 작은 경우, ranking이 우선되는 경우)

우리는 c가 아니라 predicted c인 c^에 관해서도 위의 관계가 유지되기를 바란다.

다시말해, 아래의 식이 음수이길 바라며, 그 값이 minimize 되기를 바란다.

Joachims(2022)에서 제안된 pairwise margin ranking loss는 다음과 같다. 

f(v^p, c)가 f(v^q, c) 보다 작고, 그 차가 margin보다 작으면 0이 된다. 즉, 아래의 수식과 같이 정의된다. 

 

예를 들어 margin이 3이라고 하고,

1) p와 q의 objective value가 각각 3, 4라고 하자

이 경우 그러면 두 값을 순차로 빼면 -1이고, 이는 margin과 더하면 2이다. 그러면 loss 2가 된다.  

2) p와 q의 objective value가 3 100이라고 하자. 

그러면 이 두 값을 서로 빼면 -97이고, 이는 margin과 더하면 -94가 된다, 그러면 loss가 0이된다. 

 

즉, margin의 차보다는 큰 차이만 인정하겠다..! 라는 뜻이다. 

 

다만, (11)에서 모든 S를 구하는 것은 계산적으로 매우 힘들다(5개만 존재해도 그 10개, 5C2)

그럼으로 Best-versus-rest schme을 이용해서 optimal하나 값과 나머지의 조합으로 만든다. 즉, (optimal v, v1), (optimal v, v2) .... 으로 만드는 OPc^s를 제안한다. 

그리하면 수식은 아래와 같이 변형된다. 

논문에서는 (12)가 결국 (5)에서 max(), 즉 relu form이 붙은 형태임을 보이며 결국 Mulamba et al에서 주장한 형태가 best-versus-rest의 speacial case라고 주장한다.

example 

feasible [0, 1], [1, 1], [0; 0], [1, 0]에 관해서 best vs rest 를 이용하면 pair는

([0,1], [1,1]), ([0, 1], [0; 0]), ([0,1], [1, 0])가 된다.

위에서 본 표를 보면 아래와 같다. 

feaible set V	real C: (2,-5)	c1: (-1,1)	c2: (5,11)
[0,0]	0	0	0
[0,1]	-5*	1	-11*
[1,0]	2	-1*	5
[1,1]	-3	0	-6

 

그럼으로 c1에 관해서는 pairwise loss는 max(0, 1)+ max(0, 1) + max(0, 2) = 1 + 1 + 2 = 4가 되고(제안된 pair wise, ideal pair wise의 순서대로 계산(뺄셈) 진행)

c2에 관해서는 max(0,-5)+ max(0,-11) + max(0,-16) =  0이 된다. 

Pairwise Difference loss - (13)

다른 방법으로 pairwise의 차이가 동일하게끔 loss를 설정하는 방법이 존재한다. 즉, ideal ranking에서의 차이들과 유사하게 정렬하는 것이다. 이를 pairwise difference loss라고 하며 다음과 같다. 

동일 예시를 사용하면 아래와 같이 계산된다. 

 

feaible set V	real C: (2,-5)	differnce with pair	c1: (-1,1)	differnce with pair	c2: (5,11)	differnce with pair
[0,0]	0	2	0	-1	0	5
[0,1]	-5*	5	1	-1	-11*	11
[1,0]	2	7	-1*	-2	5	16
[1,1]	-3		0		-6

 

그럼으로 각각에 관해 (2 + 1)^2 + (5 + 1)^2 + (7 + 2)^2 = 94 와  (2-5)^2 + (5- 11)^2 + (7-16)^2 = 94이다. 

Listwise Ranking

listwise ranking은 pairwise와는 다르게 entire ordered list를 다루는 방법이다. Listnet loss가 대표적으로 이는 각 항목이 최상위 항목일 확률을 계산한 다음 이러한 확률의 cross entropy loss를 정의하여 이용한다. 다만, 본 논문에서는 (4)를 그대로 사용하지 않고 Niepert et al., 2021가 제안한 아래의 loss를 사용한다.

 

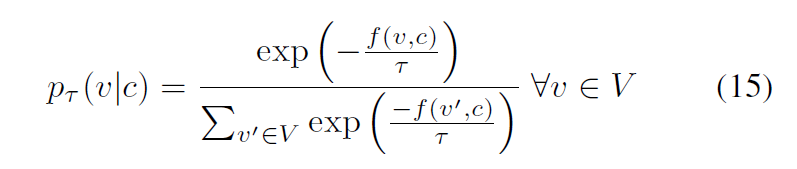
이때 타우는 distribution의 smoothness에 관여하며, 값이 0에 가가울 수록 v*(c)만 positive probaility를 가지는 카테고리컬 확률분포에 가까워지며 커질 수록 uniform distribution(균등분포)에 가까워진다. 계산의 복잡성을 줄이기 위해 V 대신 본 논문에서는 S를 사용한다(부분집합). 

 

확률분포가 주어졌을 때 listnet loss는 predicted distribution과 target 분포 사이의 cross-entropy loss로 정의된다. 이런 흐름에 따라 S의 원소 v에 관해서 cross entropy loss를 정의한다, 

또 KL divergence 식으로도 아래와 같이 정의가능하다 실제 실험 결과 큰 차이가 없었다고 한다.

 

Experiments 

실험에서는 pointwise (6) pairwise (11), pairwise difference(13) and listwise (16) ranking losses를 비교한다. 

GPU를 사용하여 ranking 알고리즘을 최적화하는 것은 가능하나, S를 구할 때는 불가능하다. 

논문에서는 Discrete combinational optimization problem 3가지를 제시한다. 

Shortest path problem과 Energy-cost Aware Scheduling, Diverse Bipartite Matching이 그것이다.

각각의 문제 세팅은 다음과 같다. 

 

Shortest path problem

5*5 path의 shortest path problem을 다룬다. 목표는 southwets에서 northeast coner로 나가는 것이고, 위 아님 우측으로만 움직일 수 있다. 이는 아래의 LP문제와 같다(기본적인 형태는 Elmachtoub & Grigas (2021) 참고)

A는 incidence matrix이고, x는 binary vector로 어떤 경로를 선택할지에 대한 선택이다(1 or 0). 

b는 25 dim의 벡터로 첫번째 원소는 1 마지막 원소는 -1이고 나머지는 0이다. 

cost vector는 mutivariage Gaussian distribution으로부터 생성된다. 

Energy-cost Aware Scheduling

CSPLib (Gent & Walsh, 1999)을 참조하여 constraint optimzation 문제 중 하나인 energy-cost aware scheduling (Simonis
et al., 1999)을 푸는 문제이다. 각 기계의 capacity를 에너지 변화에 따라 어떻게 스케줄링 할것인지에 관한 문제이다. 

보다 자세히는 J는 M개의 machine에 할당될 작업 집합이며, 이는 R 자원의 요구사항을 유지해야한다. 

각 기계 m에서 자원 r의 사용량은 그 기계의 용량을 초과할 수 없다. 

 

Diverse Bipartite Matching.

Ferber et al. (2020) and Mulamba et al. (2021)에서 풀어본 문제로 CORA cistatiation network의 데이터를 이용한 문제이다. 100개의 노드를 두개의 노드인 50개씩으로 나눈다. 보상행렬 c는 두 노그 간의 링크가 존재할 가능성을 나타낸다. n은 기사 i와 j가 같은 주제를 공유하면 1이고 아니면 0이다. p와 q는 각각 유사성과 다양성을 제약한다. 각 N1, N2의 노드는 최대 하나의 노드와 매칭된다. x는 이진변수이다(0,1). 

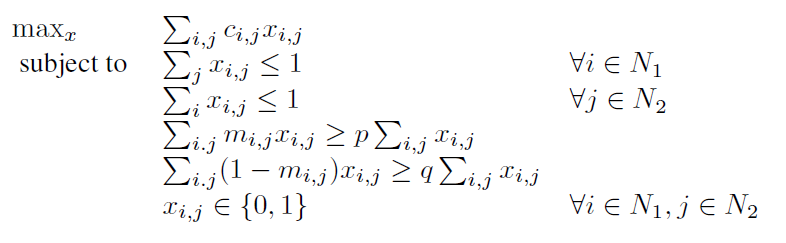
Experiments Results

metric으로 percentage regret을 이용한다. 또한 비교는 SPO+ loss (Elmachtoub & Grigas, 2021),  Blackbox backpropagation approach (Pogancic et al., 2020) and the NCE and MAP approach of Mulamba et al. (2021)가 사용된다. 또한 Twostage 방법과도 그 결과를 비교한다.

10번 반복 실행 후 그 결과의 평균을 낸 결과는 아래와 같다. 

 

Shortest pass 문제에서는 degree parameter가 증가함에 따라 regret이 올라가는 것을 확인 가능했다. degree 4, 5, 8에서는 listwise loss가 가장 작은 loss를 보였고, 작은 degree에서는 pointwise와 pairwise difference가 좋은 성능을 보였지만 degree가 증가함에 따라 regret loss가 매우 증가하였다. 

List wise loss는 energy 2와 mathing-1에서 두번째로 좋은 성능을 보이며 pairwise loss의 경우 matching-1에서 가낭 낮은 regres score를 보이며, 두 문제에서 가장 좋은 성능과 거의 유사하다. 

모든 경우 point wise의 경우 MSE(two-phase)보다도 성능이 저조한데, 이는 추가된 패널티 항이 항상 regret과 일치하지 않기 때문이다(4.2, pair wise motivation 참고). 

 

전체적으로 pariwise loss는 기본 예측 모델이 데이터 생성과 유사할 때 안정적이며, list loss의 경우 다양한 과정에서 매우 robust한 결과를 보임을 보여준다. 

 

MSE VS REGRET

그림 2를 통해 MSE와 Regret사이 상관을 보여준다. 모든 경우 pointwise의 경우는 mse를 최소화하는 것과 거의 유사한 결과를 보여준다. 다만, regret의 경우 mse(two stage)보다 큰 경우도 있다. pairwise diff의 경우 listwise와 pairwise와 비교시 더 나은 MSE를 보여준다. 

 

Psolve 비교 

P solve를 통해 최적화문제를 푸는 횟수를 줄이는 Mumba et al의 성능을 호가인한다. 

아래 table 2를 보면 psolve가 모델의 훈련 시간에 어떤 영향을 미치는지 보여준다. 

psolve가 작을 수록 그 훈련시간도 작은 이는 1) 최적화 문제를 푸는 횟수가 줌 2) ranking loss의 계산도 더 작은 수의 datapoint에 의해 계산됨

 

또한 시간은 줄었지만, pointwise를 제외하고 regret의 경우 큰 차이가 없음을 보여준다. 

 

Conclusion 

결론적으로 본 논문은 Mulamba et al을 확장하여 실행 가능한 해 집합을 caching하는 방법을 더 확장한다. 

Learn to rank 문제로 바꾼 방법을 통해 최신 기술들과 비교할만한 성능을 이룸과 동시에 그 시간적인 효율은 더 이루었다.