[Journal of Protfolio management]The Gerber Statistic: A RobustCo-Movement Measure for PortfolioOptimization(Sander Gerber et al.)

Harry M. Markowitz, 즉, 그 마코위츠 포트폴리오의 그분이 저자로 함께 작성한 자료이다(엄밀히 말하 논문..?은 아닌거 같다)

글의 요지는 기존의 공분산 행렬 추정을 더 robust한 방법으로 변경해야한다..!이며 즉, 실제 시장에는 noise가 많이 껴져있는 상태이기에 기존 방법으로 공분산 추정이 너무 오염된 상태라는 것 같다.

이를 위해 Gerber statisitc을 도입하는데(본 논문의 주저자의 이름) 자세한 건 아래에 설명한다. 

 

Introduction & Problem

포트폴리오 구성(Markowitz 1952, 1059)은 자산 수익률 간의 공분산 행렬에 크게 의존하며, 종종 smaple covariance 자체가 실제 공분산 행렬의 추정치로 이용된다(Jobson and Korkie 1980). Sharpe(1963) 이후, 계산 부담을 덜고 공분산 행렬의 통계적 특성을 개선하기 위해 다양한 모델이 사용되어왔지만 여전히 해결되지 않은 문제가 존재한다. 

Covariacne matrix를 계산하기 위해 고벰 모멘트 기반 추정치를 이용하는데 이는 수익률의 기저 분포에 극단적인 값이나 이상값이 포함될 경우 특히 문제가 된다. 이를 위해 Robust estimator가 필요하며 Tukey(1960), Hampel(1968, 1974), Huber(1977)의 연구들이 이를 보인다. 이후 Shevlyakov and Smirnov(2011)은 상관관계를 계산하는 현대의 robust한 방법론을 검토했다. 

Hampel, F. R. “Contributions to the Theory of Robust Estimation.” 1968.
Huber, P. J. “Robust Statistical Procedures.” 1977.
Tukey, J. W. “Contributions to Probability and Statistics: Essays in Honor of Harold Hotelling.” 1960.
Shevlyakov, G., and P. Smirnov. 2011. “Robust Estimation of the Correlation Coefficient: An Attempt of Survey.

 

그러나 금융 시계열의 경우 매우 nosiy하기 때문에 표준적인 robust 방법론들이 잘 맞지 않을 수 있다. 예를 들어 실제로는 의미있는 상관관계가 아닌 경우에도 non-zero entries를 가지거나 매우 극단적인 관측값이 포함되어 있을 경우 상관 추정이 왜곡 가능하다. 

그렇기에 본 방법은 특정 임계값 이하의 변동을 무시하고 동시에 극단적인 움직임의 영향을 제한하는 co-movement measure인 Gerber 통계량을 통해 이를 해결하고자한다. Gerber Statistic, GS는 움직임이 큰 경우 공동 co-movement을 인식하도록 설계되었으며, noise에 의한 작은 co-movement인 경우에는 민감하지 않도록 설계되었다. 이는 두 데이터간의 공동 움직임을 일치쌍과 불일치 쌍(number of concordant, discordant)의 개수의 차이로 측정하는 점에서 Kendall의 Tau(1938) 방법론과 유사하다. 하지만 GS는 임계값을 포함하여 임계값을 초과할 때에만 일치, 불일치로 인식하도록 변경하였다. 

 

본 자료에서는 Markowtitz의 mean-variance optimization 모델에 GS와 1) sample covariance(or Historical covariance)와 (2) 2) Leoit & Wolf shrinkage estimator와 비교한다. 

sample covariance을 사용하는 것이 robustness가 떨어지고 이상치에 매우 민감하다는 것이 잘 알려져 있으며( obson and Korkie 1980), Ledoit&Wolf의 shirnkage estimator와 비교하면 GS는 샘플 공분산 행렬을 입력으로 사용하지 않는다. 

 

Gerber Statistic

Gerber statistic에서 Gerber covariance matrix를 구하기 위해서는 Gerber Corrleation이 필요하다(상관). 

우선 표기법을 알아보자.

 

자산 혹은 증권: k= 1....K

시간 t=1, .... T 일때 r_kt는 t 시점에서의 증권 k의 수익률이다. 

각 시간 t에 관해 자산 쌍 (i,j)를 아래의 규칙에 따라 joint observation m_ij(t)로 변환한다. 

이때 H_j는 각 자산에 따라 결정되는 임계값으로 특정상수와 자산 j의 샘플 표준편차의 곱으로 결정된다(c가 크면 클수록 임계값이 높아진다, 아래의 EXHIBIT A2그림 참고, NN의 영역이 넓어짐)

즉 두 자산이 임계값을 같은 방향으로 변하는지를 보는 값이 mij이다(robust를 확보하기 위한 방법)

 

그럼 도출된 joint observation m에 간해 아레의 g statistic을 도출한다. 

이는 Kendall의 Tau 방법과 유사하며, 분모의 경우 절대값의 합을 구하는데, 이는 결국 측정된 자산의 joint observation m의 총 개수와 같다(0인 경우는 존재치 않음)

분자의 경우 단순 총합이기 때문에 두 자산 간의 움직임을 일치쌍과 불일치 쌍의 개수의 차이로 결정된다. 

 

결국은 임계값을 초과하는 정도에는 의존하지 않기 때문에(일치하는 방향에만 의존) 곱셈 모멘트 기반 측정치가 왜곡되지 않는다. 동시에 시계열이 임계값을 초과해야 계산 대상이 되기에(+1, -1이됨) noise에도 민감하지 않는다. 

 

현대 포트폴리오 이론의 기본 원칙 중 하나는 증권 수익률의 공분산 행렬이 postive semi definite하다는 것이다. 실제 데이터를 다루는 경우, 종종 이것이 맞지 않는 경우도 있음을 확인했다(3의 식을 통해 나온 g가 음인 경우). 따라서 정확하게 PSD를 생성해내는 대체 통계량을 GSij를 제안하며 이는 Equatation A-3를 보면 다음과 같다

 

Alternative Gerber Statistics(making PSD)

두 구성 요소가 같은 방향으로 이용하면서 임계값을 초과하는 쌍을 Concordant pair라고 하고, 반대 방향으로 이동하면서 임계값을 초과하는 쌍을 discordant pair라고 할때, 시계열 i,j에 개해 일치하는 쌍의 수를 $n^c_{ij}$로 불일치 쌍의 수를 $n^d_{ij}$라고 하면 방정식 3, 기존의 $g_{ij}$ 는 다음과 같이 변형할 수 있다. 

이 식은 결국 임계값 H_k = 0이라면 Kendall의 Tau 식과 동일하다. 

 

이제 두 자산 간의 관계를 아래의 그림에서 고려해보자. U는 증권의 수익률이 상한 임계값을 초과하는 경우, 즉 상승하는 경우를 나타내고, N은 증권의 수익률이 상한 임계값과 하한 임계값 사이에 있는 경우(중립), D는 증권의 수익률이 하한 임계값 아래에 존재하는 경우를 나타낸다. 행은 i를 열은 j 자산을 나타낸다고 했을 때, 아래의 그림을 다시보자.  

그럼 각 셀의 경계는 선택된 각 임계값을 의미할 것이다. 시간에 따라 각 관측치들은 9개의 영역에 걸쳐 흩어지게 되고, $n^{pq}_{ij}$를 자산 i,j의 수익률이 각각 영역 p,q에 위치한 관측치의 수라고 하면 다음과 같이 식이 변경된다.

(당연하다, UU, DD는 두 자산의 방향성이 동일하다는 것을 의미한다, UD, DU는 그 반대이다)

 

다만 Gerber matrix가 Postive semi definite이라면 수식은 아래와 같아야할 것이다. 이때 T는 관측된 전체 데이터 수를

말한다(위 수식과 아래의 수식을 비교하면 분모의 그 차이가 있다, 결국 A-3은 A-2의 분모형태에 UN NU ND DN 케이스를 더한 값이다)

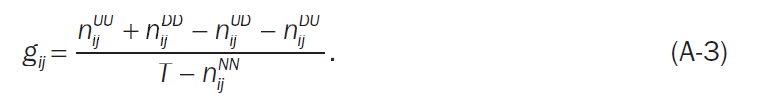
논문에서는 추가적인 설명을 다음과 같이 설명한다. 

방정식 A-3에서 Gerber 통계량의 분모를 선택한 주요 직관은 다음 관찰에서 비롯됩니다:
c가 커질수록, 더 많은 데이터 포인트가 NN 영역에 포함됩니다. 이는 통계량이 데이터의 잡음에 덜 민감하고 더 견고해지게 합니다. 우리는 이 Gerber 통계량의 특성을 데이터에서 잡음을 제거한다고 표현합니다

 

EMPIRICAL STUDY & RESULT

앞서 밝힌 것처럼 GS와 Shrinkage method와 기본 Markowitz model을 비교한다. 

본 지에서는 1988년 1월부터 2020년 12월까지 9개의 자산에 대한 월별 총 수익률(TR, total returns)을 이용하였고, MVO를 구현하기 위하여 2년간의 월별 수익률을 이용하여 포트폴리오를 초기화 한 후 이용된다. 

 

따라서 결국은 1990년 1월부터 2020년 12월까지의 기간을 기준으로 운용이 된다. 

운용 자산은 총 9가지로 아래와 같다. 

 

• S&P 500 지수 (미국 대형주; 티커 SPX)
• 러셀 2000 지수 (미국 소형주; 티커 RTY)
• MSCI EAFE 지수 (미국과 캐나다를 제외한 21개 선진국의 대형주 및 중형주; 티커 MXEA)
• MSCI 이머징 마켓 지수 (27개 신흥 시장의 대형주 및 중형주; 티커 MXEF)
• 블룸버그 바클레이즈 미국 종합 채권 지수 (국채 및 정부 관련 및 기업 증권 포함; 티커 LBUSTRUU)
• 블룸버그 바클레이즈 미국 기업 고수익 채권 지수 (티커 LF98TRUU)
• 부동산 FTSE NAREIT 전체 주식 리츠 지수 (티커 FNERTR)
• 금 (티커 XAU)
• S&P GSCI 골드만 삭스 상품 지수 (티커 SPGSCI)

이들의 상관관계는 아래와 같다. 

 

Optimization Procedure and Portfolio Backtesting

고려할 포트폴리오 최적화 프레임워크는 거래량의 0.1%, 10bp의 거래수수료를 가진다고 가정하며 다음과 같은 벡테스팅을 거친다.

- 1990년 1월부터 시작하여, 매월 초에 24개월의 회귀 창에서 현재 자산 목록의 월별 수익률을 사용하여 예상 수익률 벡터와 공분산 행렬을 추정

- Rollling window방법 사용: 모든 포트폴리오는 매월 리밸런싱,  이 리밸런싱 과정은 샘플 내 기간을 한 달 앞으로 이동시키고 다음 달을 위한 업데이트된 효율적 포트폴리오를 계산하는 Rolling window과정임

 

Results

결과는 c를 각각 0.5, 0.7, 0.9로 했을때와 모두 비교한다.

 

Gerber Statistic with c = 0.5

 

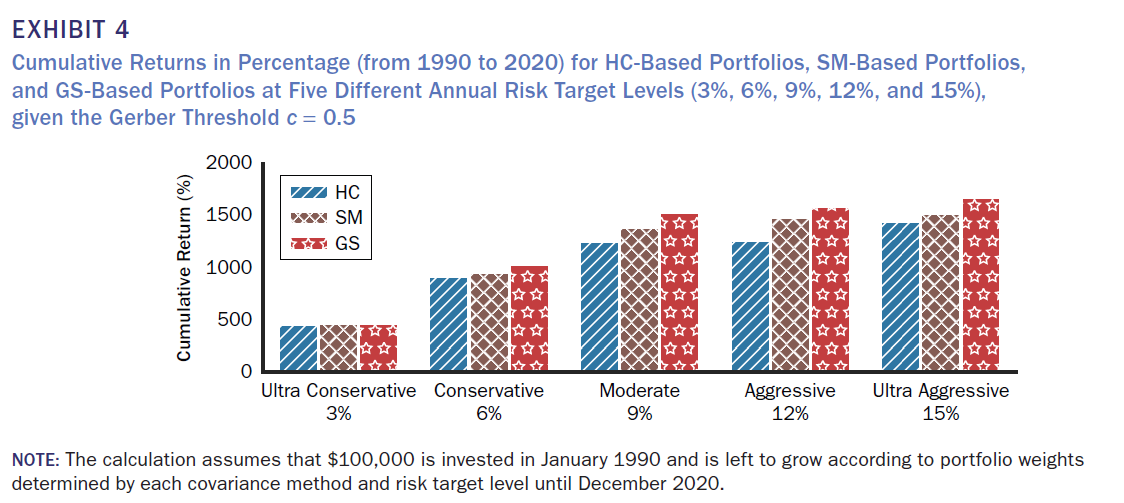
임계값 c=0.5로 설정된 GS의 주요 결과는 다음과 같다. 

1. GS는 Annualized return 기준으로 3% risk 수준을 제외하고 더 유리한 Risk-Return profile을 제공한다. 

2. Cumlative return(누적수익률) 기준으로도 동일하다. 

3. 포트폴리오 turnover, skewness와 kutosis의 경우는 HC, SM은 거의 유사하지만, GS는 3% risk 기준을 제외하고 기하평균 수익률과 sharp-ratio를 기록한다. 

4. Exhibit 6을 보면 알 수 있듯이, GS가 특정 위험 목표 수준에서 SM보다 더 높은 성과를 보인다는 것을 보여주는 것을 확인 가능하다. 

Gerber Statistic with c = 0.7

1. 모든 경우 GS가 HC와 SM보다 더 나은 profile 제공 exhibit 7참조

2. 모든 위험 목표 수준에서 더 우수한 누적 수익률 제공

3. 모든 위험 목표수준에서 더 높은 기하 수익률과 sharp ratio 제공

4. 12% 위험 목표 수준에서 GS의 평균 연간 기하 수익률은 SM보다 약 41bps 높으며, 1990-2020 기간 동안 누적 수익률은 SM보다 13.12% 높음(Exhibit 6 및 10 참조). 15% 위험 목표 수준에서 GS의 평균 연간 기하 수익률은 SM보다 약 35bps 높으며, 1990-2020 기간 동안 누적 수익률은 SM보다 11.18% 높음 (Exhibit 6 및 10 참조)

Gerber Statistic with c = 0.9

1. 모든 경우 GS가 더 나은 profile 제공

2. 모든 경우 GS가 더 우수한 누적 수익률 제공

3. 모든 경우 더 높은 기하평균 수익률과 sharp ratio 기록, 포트폴리오 회전율, 왜도, 첨도 등은 유사

4. 3%와 6% 위험 목표 수준에서 GS의 평균 연간 기하 수익률은 각각 SM보다 약 32bps 및 35bps 높음. 누적 수익률은 1990-2020 기간 동안 각각 SM보다 12.11% 및 11.67% 높음 (Exhibit 6 및 10 참조). 또한, 6% 위험 목표 수준에서 GS의 평균 연간 기하 수익률은 HC보다 48bps 이상 높다는 점도 주목할 만한 점

 

결과적으로 GS, Garber statistic은 noise에 민감하지 않기에 기존의 방법론들 보다 우수한 성능을 보여줌을 보임. 

다만, 자산 군이 시장 전체 index로 한정되어있어서 다른 자산군들에 관해 실험을 해볼 필요는 있어보임.