[Finance][Time series] Unsupervised Change Point Detection and Trend Prediction for Financial Time-Series Using a New CUSUM-Based Approach(IEEE 2022)

https://ieeexplore.ieee.org/document/9741807/

Unsupervised Change Point Detection and Trend Prediction for Financial Time-Series Using a New CUSUM-Based Approach

Abstract/ Introduction / Conclusion 등 대다수는 거의 직역했습니다 
Proposed Algrorithm, 결과 해석 등은 일부 요약 및 재정리하였습니다. 

내 마음대로 Check point

1. Kurskal Wallis를 이용한 사후검정법 제시(기존 ICSS에 추가됨)

2. Inspire을 제공한 Mann-Whiteny Statisitc 방법 확인

3. Bartlett kenrel 이용 등 기존 Kernel 관련 연구법 확인필요 

 

Abstract

본 연구의 목적은 반복적 누적 제곱합(ICSS, Iterative Cumulative Sum of Squares)을 기반으로 금융 시계열에서 변화점을 탐지하는 이진 분할 알고리즘을 제안하는 것입니다. 제안된 알고리즘인 KW-ICSS는 비모수 검정인 크루스칼-월리스(Kruskal-Wallis) 검정을 교차 검증 절차에 활용합니다. 이로 인해 KW-ICSS는 SOTA인 ICSS 알고리즘(AIT-ICSS)보다 변화점 이후의 관측치 수가 적은 비정규 분포 시계열에서도 신속하게 변화점을 탐지할 수 있었습니다. 

모의 금융 시계열(변화점의 실제 위치가 알려진)에서, KW-ICSS는 다양한 변화점 개수에 대해 평균 81%의 True Positive Rate을 기록한 반면, AIT-ICSS는 72.57%를 기록하였습니다. 또한 KW-ICSS는 서로 다른 유의 수준에서 실제 변화점과 탐지된 변화점 간 평균 절대 편차(Mean Absolute Deviation, MAD)가 AIT-ICSS보다 적었습니다. 실험 결과, 모델 파리미터 중 유의 수준(signifcance level)은 10% 미만으로 설정하는 것이 적절함을 발견할 수 있었습니다.

실제 금융 시계열에서 변화점의 정확한 위치가 알려져 있지 않은 경우, KW-ICSS는 더 적은 변화점을 탐지하고 변화점 간 간격이 더 길게 유지되는 경향을 보여 보다 강건한 탐지 성능을 나타냈습니다. 또한, KW-ICSS는 단기 트렌드 예측(prediction for the short-term)에서 평균 92.47%의 정확도를 기록했으며, AIT-ICSS는 90.69%를 기록하였습니다. 따라서 본 연구는 KW-ICSS가 AIT-ICSS의 성능을 성공적으로 개선했음을 주장합니다. 

Introduction

최근 들어 시계열 분석은 그 어느 때보다 중요해지고 있습니다. 시계열 데이터는 시스템의 운영을 시기적절하게 설명하는 요소 중 하나이며, 의료, 항공우주, 금융, 비즈니스, 광고, 서비스, 기상학, 엔터테인먼트 등 다양한 분야에서 활용됩니다. 시계열 데이터의 변화는 외부 또는 내부 요인의 영향을 받습니다.

특히, 변화점(Change Point, CP) 분석은 시계열 데이터의 분포적 특성이 변화할 때 급격한 변화를 탐지하는 것을 목표로 합니다. Change point analysis는 변화점 추정(CP estimation) 또는 변화점 마이닝(CP mining)과 밀접한 관련이 있으며, 이들은 시계열을 세분화하거나(segmenting), 이벤트를 탐지하고(event detection), 이상 징후를 감지하며(anomaly detection), 군집을 형성하는(clustering) 등의 연구를 수행하는 데 활용됩니다.

 

또한, 변화점 분석은 금융 분야에서 투자 전략을 수립하는 데 중요한 역할을 합니다. 예를 들어, 포트폴리오 투자 의사 결정(Decision making)은 시장이나 자산 가격의 모멘텀 변화 예측을 고려하여 이루어질 수 있습니다. 데이터 과학 시대에 접어들면서, 시장 모멘텀 변화를 예측하기 위한 다양한 노력이 정량적 및 정성적 접근 방식 모두에서 이루어지고 있습니다. 예를 들어, 평균 수익률, 변동성 및 조건부 상관관계의 변화점을 동시에 탐지하고 예측하는 연구가 수행되었습니다

대부분의 관련 연구들은 정상성(stationarity)을 유지하며 비모수적(non-parametric) 방법을 활용하여 금융 시계열을 유사한 특성(예: 평균, 분산, 상관관계)을 갖는 세그먼트로 분할, 변화점을 추정하는 데 중점을 둡니다.

 

구체적으로, 변화점 분석은 실시간(온라인, online) 방법과 회고적(오프라인, offline) 방법으로 구분될 수 있습니다.

우선, 온라인 방식은 이벤트 탐지(event detection) 또는 이상 탐지(anomaly detection) 와 관련이 있습니다. 이는 시계열의 동적 변화를 실시간으로 탐지하거나 예측하는 것을 목표로 합니다.

반면, 오프라인 방식은 신호 분할(signal segmentation) 과 관련이 있으며, 과거 시계열을 해석하고 설명하기 위해 모든 변화점을 탐지하고 분석하는 데 초점을 맞춥니다. 즉, 오프라인 방식은 전체 데이터셋을 한 번에 고려하거나, 특정 기간별로 배치(batch) 단위로 분석하여 가능한 모든 변화점을 추정하는 방식입니다.

 

본 연구에서는 오프라인 방식을 기반으로 이진 분할(binary segmentation) 알고리즘을 개발하여, 오프라인 분할(segmentation)과 온라인 추세 예측(trend prediction)의 성능을 동시에 개선하고자 합니다.

이진 분할을 이용한 변화점 추정 연구에서는 일반적으로 확률 분포 변화(probability distribution change), 우도 함수(likelihood function) 기반 분석, F-검정을 이용한 비교 검증(comparison verification using F-test) 등을 활용하여 변화점을 탐지합니다.

또한, 베이지안(Bayesian) 방법과 누적합(CUSUM, Cumulative Sum) 방법 역시 시계열의 변화점을 추정하는 데 사용되어 왔습니다.

 

본 연구에서 제안하는 알고리즘은 반복적(iterative) CUSUM 방법을 활용하여, 데이터의 분포가 정규성을 벗어나는 지점을 변화점으로 탐지합니다.

CUSUM 기반 알고리즘의 효과는 석유 가격과 미국 달러 환율 간의 인과관계 분석, 시간에 따른 관계 변화 분석, 변동성 전이 효과 분석 등에 활용되면서 입증되었습니다. 또한, 통합 누적 제곱합(ICSS, Integrated Cumulative Sum of Squares) 알고리즘이 유가 변동성(asymmetric volatility in oil prices) 분석에 효과적임이 밝혀졌습니다.

이러한 알고리즘은 상품 시장(commodity market), 주식 시장(stock market), 외환 시장(foreign exchange market), 역외 시장(offshore market) 간의 관계를 분석하고 예측 성능을 개선하는 데 적용되었습니다.

그러나 초기 ICSS 방법에는 몇 가지 제한점이 존재합니다.

1. 데이터가 정규분포를 따른다고 가정한다는 점
2. 데이터 크기와 규모에 따라 변화점 탐지의 강건성(robustness)이 불확실하다는 점
3. 변화점의 개수를 사전에 알 수 없다는 점

이러한 한계를 극복하기 위해 CUSUM 알고리즘은 지속적으로 개선되어 왔습니다.

 

1.  첫째, 베이지안 규칙(Bayesian rule) 을 적용하여 ICSS 알고리즘의 정규성 가정(normality assumption) 문제를 해결하려는 연구가 진행되었습니다. 추가적으로 순차적 체제 변화 탐지(SRSD, Sequential Regime Shift Detection) 방법이 개발되어, 이상치(outliers)에 민감한 ICSS 알고리즘이 도입되었습니다. 베이지안 규칙 기반 ICSS와 SRSD는 변화점 탐지에 효과적임이 검증되었습니다. CUSUM 통계를 활용한 두 표본 검정(two-sample testing technique)과 ICSS를 결합한 비모수적(non-parametric) 변화점 탐지 모델이 개발되어, 정규분포를 따르지 않는 데이터에도 효과적으로 적용될 수 있도록 개선되었습니다.

CUSUM과 첨도(kurtosis) 통계를 결합한 AIT-ICSS(Advanced ICSS) 알고리즘이 개발되었습니다. 특히, AIT-ICSS는 에너지 시장 변동성 예측(volatility forecasting)에서 더 나은 성능을 보이는 것으로 나타났으며, 변화점을 더미 변수(dummy variables)로 활용하는 방식이 효과적이라는 연구 결과가 보고되었습니다. 하지만, 장기 기억(long memory) 데이터에서는 변화점이 과소평가될 가능성이 있다는 점이 지적되었습니다(ps: 과소평가란 말은 문맥상 CP를 적게 찾음을 의미)

 

2.  ICSS의 시간 창(time-window) 기반 추정 방식으로 인해 강건성이 낮아지는 문제를 해결하기 위한 다양한 연구가 이루어졌습니다. 예를 들어, 베이지안 분석(Bayesian analysis)과 변화점이 포함된 선형 모델(linear models incorporating CPs)을 활용하면 분포 추정의 정확성을 향상시킬 수 있습니다. 또한, 적절한 시간 창 크기(time window size)를 설정하는 것이 알고리즘의 강건성을 향상시키는 데 도움이 될 수 있으며,  다중 창(multi-window) 방법을 활용하면 변화점 탐지의 일관성을 개선할 수 있음이 입증되었습니다.

 

3. CP의 개수를 추정하기 위하여 회귀 분석(regression analysis)에서 회귀 계수 및 잔차(residuals)의 분산 변화를 고려하는 방법이 제안되었으며, ICSS가 비정규 분포 데이터나 추세(trend)가 있는 데이터에서는 강건성이 떨어진다는 문제가 제기되었습니다. 이를 해결하기 위해 잔차(residuals)나 부트스트랩(bootstrap) 이론을 활용하여 강건성을 높이는 방법이 제안되었습니다. 

이와 더불어, 변화점을 보다 정교하게 탐지하기 위한 연구가 지속되고 있습니다. 예를 들어, 웨이블릿(wavelet) 기반 변동성 구조 변화를 분석하는 알고리즘이 개발되었으며, 농장 동물의 행동 패턴 분석에 적합한 새로운 알고리즘이 제안되었습니다([46] S. Breitenberger, D. Efrosinin, W. Auer, A. Deininger, and R. Waßmuth, ‘‘Change point detection in piecewise stationary time series for farm animal behavior analysis,’’ in Operations Research Processing. Springer, 2017, pp. 369–375)

변화점 탐지는 일반적으로 급격한 변화(sharp change)를 탐지하는 데 초점을 맞추지만, 최근 연구에서는 완만한 변화(smooth change)까지 감지할 수 있는 방법을 개발하고 있으며, 이러한 방법들이 비정규 분포 데이터에서도 효과적임이 검증되었습니다( [47] R. Ben Hajria, S. Khardani, and H. Raïssi, ‘‘Testing for abrupt breaks in variance structures with smooth changes,’’ Commun. Statistics-Theory Methods, vol. 4, pp. 1–18, Oct. 2018. [48] Z. Gao, Z. Shang, P. Du, and J. L. Robertson, ‘‘Variance change point detection under a smoothly-changing mean trend with application to liver procurement,’’ J. Amer. Stat. Assoc., vol. 114, no. 526, pp. 773–781, Apr. 2019)

Wavelet Transform: 웨이불릿 함수를 이용하여 시간-주파수 영역에서 시계열 데이터를 변환하여 분석/ Non sationary 데이터에 더 적합하다고 함

 

본 연구의 목표는 변화점 탐지 성능과 금융 시계열에 적합한 온라인 이진 예측(binary prediction) 기능을 통합적으로 개선한 새로운 ICSS 알고리즘, KW-ICSS를 제안하는 것입니다.

제안하는 알고리즘은 CUSUM 기반 방식을 따르며, 정밀도-재현율 곡선(precision-recall curve, PR 곡선)의 F1 점수 또는 수신기 작동 특성(ROC) 곡선의 면적(AUC) 측면에서 높은 성능을 기록한 알고리즘 중 하나입니다. 

특히, AIT-ICSS는 비모수적 커널 기반 방법(non-parametric kernel-based method)으로서, 정규성을 따르지 않는 데이터에도 적용 가능하다는 장점이 있어 본 연구에서는 AIT-ICSS를 벤치마크 모델로 활용하였습니다. 

KW-ICSS 알고리즘은 AIT-ICSS와 마찬가지로 비모수적 접근법을 활용합니다. 하지만, AIT-ICSS에서 사용된 Mann-Whitney 통계를 확장한 크루스칼-왈리스(KW) 검정을 결합하여, 비정규 분포 데이터에도 적용 가능한 방식으로 개선되었습니다.

 

본 연구의 기여점은 다음과 같습니다.

 

첫째, KW-ICSS의 변화점 탐지 및 추세 예측 성능이 시뮬레이션 금융 시계열 데이터에서 개선됨을 확인하였습니다. 시뮬레이션 데이터는 변화점의 실제 위치를 사전에 지정할 수 있어 탐지 성능을 정량적으로 평가하는 것이 가능합니다. 실험 결과, 변화점과 탐지된 변화점 간 평균 절대 편차(mean absolute deviation)를 최소화하려면 모델의 유의수준(α)을 10% 이하로 설정하는 것이 적절함을 발견하였습니다.

둘째, KW-ICSS의 변화점 탐지 강건성이 다양한 실제 금융 시계열 데이터에서도 확인되었습니다. 주식, 국채, 통화, 원자재 시장에서 18년간의 금융 데이터를 활용하여 실험을 수행하였습니다. 실제 금융 데이터에서는 변화점의 정확한 위치를 알 수 없기 때문에, AIT-ICSS의 단점으로 알려진 변화점 과다 탐지(over-estimation) 현상을 비교 분석하였습니다. 실험 결과, KW-ICSS는 대부분의 금융 시계열에서 변화점을 더 적게 탐지하며, 변화점 간의 간격이 더 길어지는 특징을 보였습니다.

셋째, 제안한 알고리즘의 추세 예측 성능이 실제 금융 데이터에서도 향상됨을 확인하였습니다. 일부 사례에서는 예측 성능이 다소 낮게 나타났지만, 대부분의 금융 시계열에서는 10% 이하의 유의수준에서 예측 성능이 향상됨을 확인할 수 있었습니다.

 

Proposed Algroithm

A. SINGLE BINARY SEGMENTATION PROCESS

시계열 데이터를 우선 아래와 같이 정의하자. 

이때 X는 N dim의 벡터로 정의하고, 1.. T 까지의 시간을 가진다. 이때 각 시계열 데이터는 위와 같이 표현 가능한데 

u는 각 시계열(N 차원 중 하나의 차원)의 평균값, R은 평균이 0이고 Postive definite covariance matrix를 가지는 random값이다(흔히 이야기하는 입실론 값인듯하다). 

 

CP analysis는 앞선 글에서 다룬 것 처럼  아래의 귀무가설과 대립가설을 가진다. 

 

이제 위의 가설을 검정하기 위해 iterative segmentation, 반복 분할 과정을 통해 검정이 이루어진다. 

 

1. 초기 변화점 탐색(Initial CP Detection)과 반복적 분할(Iterative Segmentation)에서는 전체 샘플 기간 중 가장 높은 우도를 가진 change point를 분석하여 세그먼트를 추정한다.  변화점을 기준으로 두 개의 세그먼트(Segment)로 나눈뒤 탐지된 변화점을 기준으로 앞쪽(Forward)과 뒤쪽(Backward) 방향에서 추가적인 변화점 탐색 이 과정을 반복하여 가능한 모든 변화점을 탐지(사실 N번 반복하면 아래의 B, muliple CPs이다, 단일 과정을 하면 single이다)하고, 이를 "초기 변화점(Initial CP)"으로 설정. 

 

2. 교차검증 (Cross-Validation)에서는 이 iniital point를 검정한다. 이를 위해 각 CP들의 앞뒤 구간을 subsample periods로 설정한후 다시 앞뒤로 분할한 뒤 CUSUM을 계산하여 해당 CP의 유효성을 검증한다. 만일 새롭게 탐지된 cp가 기존의 cp와 동일한 경우거나 새롭게 탐지된 cp가 없는 경우 이를 최종 변화점이라고 한다(final cp). 반면 아닌 경우 이는 오류로 간주하여 오류가 0으로 수렴할 때 까지 변화점을 업데이트한다. 

 

CUSUM 검정에 사용되는 CUSUM 검정통계량은 아래와 같이 정의된다. 

여기서 k가 0이거나 T이면 D는 0이다. 

 

기존 연구에서는 D를 이용한 CP 추정이 정규 분포를 따르지 않는 데이터(non-normal distribution data)에서 첨도(kurtosis)가 크고 조건부 이분산성이 존재할 경우 효과적이지 않음을 보였었다( A. Sansó, ‘‘Testing for changes in the unconditional variance of financial time series,’’ Revista Economía Financiera, vol. 4, no. 1, pp. 32–53, 2004). 이를 해결하기 위해 바틀렛 커널(Bartlett kernel)을 기반으로 한 비모수적(non-parametric) 통계량을 적용한 변형된 D' 가 아래와 같이 제안되었다. 

데이터에 급격한 구조적 변화가 없다면 D'은 0을 중심으로 진동하고, 구조적 변화가 있다면 특정 임계범위를 벗어나게 된다. 따라서 알려지지 않은 변화점(unknown CP)을 추정하는 마지막 단계에서는 다양한 유의수준(significance level, α)에 대한 임계값(critical values) 을 설정해야하며 기존 연구에서는(바로 위의 논문) 해당 통계량의 95 백분위 수가 1.4058이라는 것을 보였고 해당 값을 검정통계량이 초과하면 귀무가설을 기각한다. 

 

이때 변화점은 아래와 같이 결정된다.

B. ITERATIVE SEGMENTATIONS FOR MULTIPLE CPs

앞서 살펴본 방법은 최대값을 가지는 단 하나의 변화점을 탐지하는 방법론이기에 다중 변화점(multiple cps)를 찾기 위해서는 아래의 대립가설을 풀어야할 것이다. 

이를 위해 Greedy Iterative Binary Segmentation을 사용할 수 있다. 

 

1. 전체 기간을 대상으로 단일 변화점(single CP)을 탐지.
2. 만약 변화점이 탐지되지 않으면, 알고리즘을 중단하고 귀무가설 H0​ 을 채택.
3. 반면, 변화점이 탐지되면 시계열 데이터를 두 개의 세그먼트(segments)로 나눈다
4. 분할된 각 세그먼트 내에서 추가적인 변화점 탐지를 반복하고 탐지된 경우 다시 세그먼트를 분할한다(새로 찾은 CP 기준으로) 이는 H0가 채택될때까지 반복된다. 

이진 분할 알고리즘은 O(NlogN) 알고리즘이라 빠르지만 변화점을 과대추정하는 경향이 있기에 이에관한 신뢰도 검증이 추가적으로 필요하다. 

C. CROSS-VALIDATION OF MULTIPLE CPs USING THE Kruskal–Wallis TEST

앞서 말한 것처럼 과대추정을 막기 위하여 기존의 ICSS 분할 알고리즘(ICSS segmentation algorithm) 은 변화점의 신뢰도를 검증하기 위해 교차 검증(cross-validation) 단계를 포함한다. 이는 A에서 밝힌 부분과 같이 오류가 0으로 수렴될 때까지 반복된다. 

본 논문에서는 이 검증 단계에서 크루스칼-왈리스 Test를 사용한다. 이는 비모수 검정의 대표적 방법이며 이는 중앙값을 기준으로 검정일 진행한다. 

기존의 AIT-ICSS와 비교하였을 때, AIT-ICSS는 비모수적(non-parametric) 방법을 활용하지 않으며, 정규성 가정(normality assumption)에 의존하나 이에 반해, 크루스칼-왈리스 검정(KW test)은 분포의 정규성을 가정하지 않고 두 개 이상의 독립 샘플을 비교하여, 이들 샘플이 동일한 분포를 가지는지 검증한다, 

 

즉 정리하면

1. 정규분포 가정→ 비정규 분포(non-normal distribution) 데이터에도 적용 가능
2. 많은 양의 데이터가 필요함  → 관측치 수가 적은 경우에도 비교적 정확한 검정 수행 가능, 실시간(online) 변화점 탐지에 활용 가능

 

Kruskal wallis 검정은 아래의 귀무 대립가설을 가진다. 

 

• 귀무가설(H0​): 모든 그룹의 중앙값은 서로 같다.  -> 변화점 앞뒤의 두 구간이 동일한 분포 를 갖는다.
• 대립가설(H1): 모든 그룹의 중앙값이 전부 같은 것은 아니다 -> 변화점 앞뒤의 두 구간이 서로 다른 분포를 갖는다.

귀무가설이 기각되면, CP가 업데이트된 CP로 선택되며 이 과정은 초기 CP와 업데이트된 CP 간의 오류가 0으로 수렴할 때까지 반복되며, 결과적으로 최종 CP가 선택된다(앞선 부분과 동일). KW 검정 통계량은 다음과 같이 계산될 수 있다. 

 

 

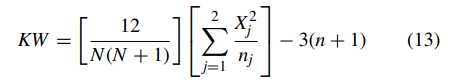
데이터 내의 동일한 값(tie)가 다수 존재하는 경우 다음과 같이 변형된 KW 통계량을 사용할 수 있다. 

이때 kj는 j번째 세그먼트에서 tie의 개수이다. 

 

여기서 짚고 넘어가야할 것은 KW 검정은 교차 검증 과정에서만 사용되며, 초기 CP 구성 단계에서는 사용되지 않는다. 이는 KW 검정이 과대평가하는 경향이 있기 때문이다. 즉, KW 검정은 최소한의 데이터만으로도 CP를 추정할 수 있다. 그러나 이를 평가 과정에서만 사용하면 강건성을 향상시킬 수 있다. 기존 알고리즘 또한 검증 과정을 포함하고 있지만, 정성적 방법(시각적, 혹은 상대비교를 의미하는 듯)을 사용하거나 특정 오류를 무시하는 방식 등으로 엄격하지 않기에 따라서 본 연구에서는 비모수적 KW 알고리즘을 통해 이를 보완한다. 

최종적으로 위와 같이 유의수준을 통해 가설을 기각하거나 채택한다. 이때 χ2와 α 모두 카이제곱분포를 따른다(정확히는 카이제곱 임계값과 유의수준이다)

 

D. PERFORMANCE EVALUATION FOR TREND PREDICTION

앞서 밝힌것처럼 본 연구에서는 Trend prediction, 추세 예측 성능을 AIT-ICSS와 비교하여 평가한다. 추세 예측, 즉 Trend Prediction에 관하여 본 연구에서는 다음과 같이 정의한다. 

변화점이 탐지된 시점 t*에 관하여 해당 시점의 전후의 평균을 계산하여 X1과 X2바를 계산한다. 

이는 아래와 같이 정의된다. 

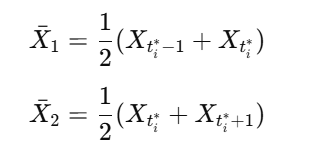
즉 변화점이 탐지된 후 t* + 1 시점에서 추세 예측이 가능하다. 이는 변화점이 존재하는 경우 과거 추세가 변화하는 전환점(turning point)으로 작용할 가능성이 높다는 가정을 기반으로한다. 따라서, 기존 데이터만을 활용하여 미래 추세를 예측할 수 있으며, 학습(train)과 테스트(test) 데이터로 나누는 지도학습 과정이 필요치 않다. 

추세 예측 성능을 평가하기 위해, 실제 금융 시계열의 진짜(truth) 추세를 정의하면 아래 와 같다. 

CUSUM 검정을 활용하여 실제 추세를 검증 정의할 수 도 있지만, 이는 초기값과 이상치, 변화점 개수의 영향을 받을 수 있기에 적절치 않다. 따라서 본 연구에서는 MACD(Moving Average Convergence-Divergence) 필터를 활용하여, 금융 시계열의 변동 방향을 측정한다. MACD는 최근 데이터에 더 높은 가중치를 부여하는 지수 이동 평균(EMA, Exponential Moving Average) 기반 지표이며,특정 기간 내 시계열의 국소(local) 움직임과 연속적인 변동성을 추정하는 데 활용된다.

 

MACD는 다음과 같이 정의 된다.

우선 EMA(Exponential moving avergage)를 정의한다. 이때 l은 lag parameter이다(Lag Parameter는 이동평균을 계산할 때 고려하는 시간 간격)

 

MACD는 단기 지연(l2) EMA와 장기 지연(l3​) EMA 간의 차로 정의된다.

 

 

추세 지표(TI, Trend Indicator) 는 MACD 시퀀스의 단기 지연(l1) EMA를 원래의 MACD(t)간의 차로 계산되며 이는 아래와 같이 정의된다. 여기서 l1 < l2 < l3이다(시간의 길이). TI는 여러번의 차분을 포함하기에 CP 주변구간에서의 2차 미분(second derivative) 과 유사한 역할을 한다. 

 

 

본 연구에서는 시간 시계열의 미래 방향을 예측하는 단기 미래 추세 지표를 활용한다. 단기 미래 미래 시간 지평 h에 관한, t~t+h까지의 누적 추세 지표값인 TI는 다음과 같이 정의됩니다

 

연구에서는 h=10 으로 설정하여 변화점 탐지 후 10단위 기간 동안의 누적 변동 방향을 측정합니다.

• TI(t*+h) > 0이면, 실제 추세가 상승(upward trend)
• TI(t*+h) < 0이면, 실제 추세가 하락(downward trend)

이제, KW-ICSS와 AIT-ICSS 알고리즘이 탐지한 변화점에서의 시계열 방향과 실제 추세(TI) 간의 일치 여부를 비교하여,
각 알고리즘의 추세 예측 성공률(success rate)을 평가할 수 있습니다.

RESULTS & DISCUSSIONS

A. 시뮬레이션된 금융 시계열에서의 성능 (PERFORMANCE ON SIMULATED FINANCIAL TIME-SERIES)

제안된 알고리즘의 특성과 성능을 평가하기 위해 우선 모의 금융 데이터를 기반으로 분석한다. 

모의 데이터를 사용하는 이유는 우선 CP 탐지가 비지도 학습 문제이기에 성능평가가 어려우나 시뮬레이션 데이터를 사용하면 실제 변화점 위치를 사전에 정의할 수 있어 평가에 용이함. 또한 시계열에서 CPD 알고리즘의 매개변수의 특성을 확인하고 적절한 매개변수를 찾고 평가하기 위해서이다. 

 

- 데이터 생성 규칙

 

모의 데이터는 ARMA 알고리즘을 이용하여 생성하였으며(56-60 참고문헌 참고)이는 데이터의 평균과 분산을 적절히 추정한다 [61]–[65]. 본 연구에서는 ARMA(1,1) 프로세스를 사용, N = 1000인 100개의 시계열 샘플을 생성하였다. 

이는 Python 3.8.5 환경에서 statsmodels 패키지의 ARMA 샘플 생성 함수를 사용하였고, 함수의 매개변수는 기본값으로 설정되었으며, 자기회귀(AutoRegressive) 및 이동평균(Moving Average) 계수는 0과 1 사이의 값으로 설정되어 정상성을 만족하는 데이터를 생성하였다. 또한 생성된 데이터는 CP 개수를 반영하되 평균 범위의 일관성을 유지하게 하였다. 

 

조금 더 자세히는 CP가 하나인 경우 이전과 이후 존재하는 두 기간에 관하여 각 기간의 평균 값은 0과 1 중 하나로 선택된다. 만일 CP가 2개 이상인 경우 각 기간의 평균값은 중복없이 0, 1, 2 중 무작위로 선택되며 평균 변화의 범위( 구간 간 평균값 차이가 보통 1이지만, ARMA 모델을 사용하여 데이터를 생성할 때 평균값이 정확히 0, 1, 2가 아니라 그 주변에서 조금씩 변동할 수 있도록 조정된다는 의미)는 평균 구간의 절반인 0.5로 제한하여 CP 인전과 이후의 평균 크기가 이를 벗어나지 않도록 하였다. 

간단히 예를 들어 구간 A 평균: 2,구간 B 평균: 0,구간 C 평균: 1로 생성하는 것이 아니라 구간 A의 평균: 0.8 구간 B의 평균: 1.3 (변화량: 1.3 − 0.8 = 0.5 1.3−0.8=0.5) 구간 C의 평균: 1.9 (변화량: 1.9 − 1.3 = 0.6 1.9−1.3=0.6)로 너무 급격한 변화를 방지하고 보다 현실적인 데이터를 생성함 

 

- 알고리즘 평가

 

알고리즘 평가, 즉 CPD 성능은 아래의 두가지 지표를 통해 평가된다. 

 

• 참양성 비율(True Positive Rate, TPR)
  • 탐지된 변화점이 실제 변화점과 ±5 범위 내에 위치할 경우, 탐지 성공으로 간주
  • TPR이 높을수록 변화점 탐지 성능이 우수함을 의미
• 평균 절대 편차(Mean Absolute Deviation, MAD)
  • 탐지된 변화점과 실제 변화점 간의 거리(오차)의 절대값을 평균하여 계산
  • MAD 값이 작을수록, 변화점 위치를 정확하게 탐지했음을 의미

CP의 총 개수를 Number of CP 줄여서 NCP라고 하자. 이는  변화점의 개수를 의미하며 [0, 5]의 범위를 가진다. 최대값이 5인 이유는 MAD가 1미만이 되는 기준을 충족하기 때문이다. 각 CP는 시간 ti∗​=(iN)/NCP에서 설정되며, 이때 i는 [1,NCP-1]이다. 

각 부분은 앞서 말한 것처럼 중복없이 집합 [0, 1, ... NCP] 에서 무작위로 선정되며 실험에서 교차 검증의 유의수준은 기본적으로 5%로 설정되었다. 

 

아래의 Figure 1은 모의 시계열에서 서로 다른 CP 개수에 따른 시뮬레이션 스냅샷이다, 

• 검은색 수직선(black vertical lines): 시뮬레이션 데이터에서 사전에 정의된 실제 변화점(true change points)
• 파란색 실선(solid blue line): 탐지된 변화점 이후 상승 추세(upward trend)
• 빨간색 점선(dashed red line): 탐지된 변화점 이후 하락 추세(downward trend)

AIT-ICSS(좌측)과 KW-ICSS(우측) 비교 시 KW-ICSS가 보다 정확한 탐지를 제공함을 그림에서 알수 있다. 

• 변화점 개수가 3개 이상일 경우(NCP=3,4,5N_{CP} = 3, 4, 5NCP​=3,4,5), AIT-ICSS는 과도한(overestimated) 변화점을 탐지하는 반면, KW-ICSS는 보다 정밀한 탐지 결과를 보여준다
• 따라서, KW-ICSS는 AIT-ICSS보다 변화점 탐지의 강건성(robustness)이 우수함을 확인

 

 

FIGURE 1. Detected CPs for AIT-ICSS (left) and KW-ICSS (right) in simulated time-series

다음으로, 100개의 모의 금융 시계열에서 CP 탐지 결과를 Table 1에 요약하였다.하였다. 두 알고리즘 모두 CP 개수가 증가할수록 TPR이 증가하는 모습을 확인 가능하다. 

Table 1에서 굵은 글씨는 더 우수한 성능을 나타낸다. 각 지표별로 결과는 아래와 같이 요약 가능하다. 

 

• TPR(True Positive Rate, 참양성 비율)
  • TPR 계산 시, 탐지된 CP가 설정된 CP 주변 ±5 이내면 성공으로 간주
  • 변화점 개수가 증가할수록 TPR이 증가하는 경향을 보임
  • CP가 하나인 경우 AIT-ICSS와 KW-ICSS의 TPR은 각각 35%와 65%로, KW-ICSS가 CP 탐지 성능을 크게 향상됨
  • KW-ICSS는 모든 변화점 개수에서 AIT-ICSS보다 높은 TPR을 기록, 평균적으로 AIT-ICSS(35%–82%) 대비 KW-ICSS(65%–86%)가 우수한 탐지 성능을 보임
• MAD(Mean Absolute Deviation, 평균 절대 편차)
  • MAD 값이 낮을수록 탐지된 CP와 실제 CP의 절대차임으로 변화점 탐지의 정확성이 높음을 의미
  • 대부분의 경우, KW-ICSS의 MAD 값이 AIT-ICSS보다 낮았으며, 특히 변화점 개수가 적을 때 더욱 두드러진 차이
  • 단, NCP=4 인 경우 KW-ICSS의 MAD가 AIT-ICSS보다 높게 나타났는데, 이는 3번째(CP3) 및 4번째(CP4) 변화점 탐지의 정확성이 상대적으로 부정확하게 탐지하여 크게 증가
• 단기 미래 추세 예측 성능 (short-term future sucess rate)
  
  • h=10의 방향 예측 성공률을 기준으로 평가, 값이 클수록 우수함을 의미
  • 두 알고리즘 모두 CP 개수 증가시 성공률이 증가
  • KW-ICSS는 모든 변화점 개수에서 AIT-ICSS보다 높은 단기 추세 예측성능 을 기록, 평균적으로 AIT-ICSS(81%–96%) 대비 KW-ICSS(90%–98%)가 우수한 탐지 성능을 보임

TABLE 1. Performances of CP detection and trend prediction for AIT-ICSS and KW-ICSS algorithm in simulated financial time-series.

 

Figure 2는 다양한 CP개수에 대한 전체 MAD의 박스플롯을 나타내며, 다양한 유의수준 α에서의 MAD 분석 결과는 아래와 같다. 

이는 모의 금융 시계열의 CP가 알려져 있기 때문에 가능하다. 

일반적으로, 유의 수준이 증가할수록 MAD도 증가하는데, 이는 높은 유의 수준에서 CP가 과대평가될 위험이 있음을 나타낸다. 두 알고리즘 모두 11% 이상의 유의 수준에서 MAD가 눈에 띄게 증가하므로, 정확한 CP 탐지를 위해 유의 수준을 10% 이하로 유지하는 것이 바람직하다. 또한, 모든 유의 수준에서 KW-ICSS가 AIT-ICSS보다 우수한 성능을 보였다.

B. 실제 금융 시계열 데이터에서의 성능 (PERFORMANCE ON REAL-WORLD FINANCIAL TIME-SERIES)

- 데이터 분석 

실제 데이터 실험에서는 KW-ICSS 알고리즘을 평가하기 위해 32개의 금융 시계열에 대한 5563일(N = 5563)의 일일 종가 데이터를 사용하였다. 해당 데이터는 주식(13개), 국채(7개), 통화(6개), 원자재(6개) 시장에서 가져왔으며, 2001년 1월 1일부터 2020년 12월 31일까지 18년 동안의 일일 종가 데이터를 포함한다. 데이터는 Thomson Reuters Datastream에서 수집되었다.

 

Figure 3은 min-max 스케일링을 적용한 전체 금융 시계열을 나타낸다. 결과에 따르면, 각 시장은 서로 다른 움직임과 구조적 변화를(즉, CPs가 존재) 보인다. 먼저, 실제 금융 데이터에서 이러한 구조적 변화가 존재하는지 확인하기 위해 통계 검정을 수행하였다.

실제 금융 시계열의 CP의 정확한 위치는 알려져 있지 않다. 그러나 간접적인 검증을 통해 CP의 존재 여부를 확인할 수 있다. 예를 들어, 구조적 변화가 발생하면 시계열 데이터는 정규 분포를 따르지 않을 수 있으며, 이는 시간에 따른 추세 변화 또는 분산 변화를 의미할 수 있다. 이러한 맥락에서, 기술 통계를 검토하고, 정규성(normality), 이분산성(heteroscedasticity), 정상성(stationarity) 검정을 수행하였으며, 결과는 Table 2에 요약되었다.

 

먼저, 각 부문의 평균과 분산이 다르며, 대부분의 시장이 양의 왜도(skewness)를 가진 것으로 나타났다. 또한, 대부분의 시장은 0이 아닌 첨도(kurtosis) 값을 가지므로 비정규(Gaussian) 분포를 따르지 않는 것으로 확인되었다.

둘째, 분산의 동일성을 검정하는 ARCH 검정에서, 시차(lag) 10과 20에서 1% 유의 수준에서 귀무가설(H0)이 강하게 기각되었다. 이는 금융 시계열의 분산이 일정하지 않음을 의미한다.

마지막으로, 모든 시장의 가격 시계열은 비정상성(non-stationary)을 보였다. 이는 Augmented Dickey-Fuller (ADF) 검정에서 귀무가설(H0)이 기각되지 않았기 때문이다. 즉, 금융 시계열은 추세(trend), 분산(variance), 계절성(seasonality) 등의 요인으로 인해 일정한 구조를 가지지 않는 것으로 나타났다.

 

- 알고리즘 평가

모의 금융 시계열 실험과 유사하게, 실제 금융 시계열에도 AIT-ICSS 및 KW-ICSS 알고리즘을 적용하였다. 모의 데이터와 실제 금융 시계열 간의 주요 차이점은 CP의 실제 위치가 알려져 있지 않다는 점이다. 따라서 탐지된 CP의 개수와 예측 성능을 기준으로 CP의 과대탐지(over-estimation) 개선 및 추세 예측 능력 향상 여부를 분석하였다.

 

- CP의 과대탐지(over-estimation) 개선 및 추세 예측 능력

먼저, 서로 다른 금융 시장에서 탐지된 CP의 대표적인 사례를 유의 수준 α=5%에서 Figure 4에 나타냈다. 여기서 파란 실선은 CP 이후의 상승 추세, 빨간 점선은 하락 추세를 의미한다. 두 알고리즘(AIT-ICSS, KW-ICSS) 모두 탐지된 CP 이후 시계열의 움직임 변화를 시각적으로 확인할 수 있다.

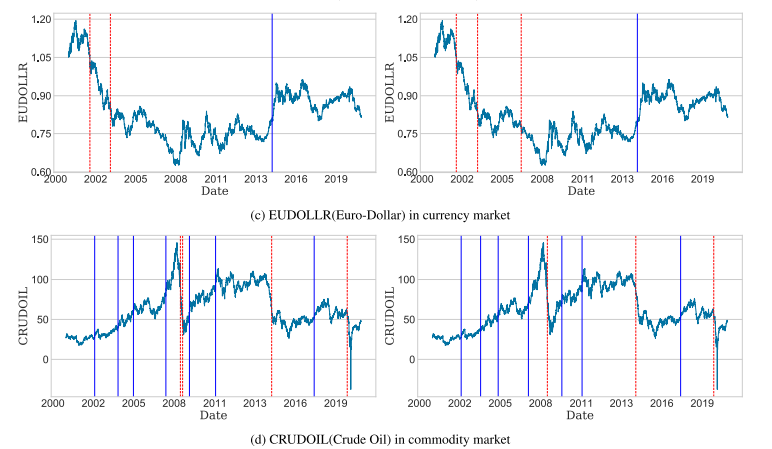
FIGURE 4. Representative cases of the detected CPs of AIT-ICSS (left) and KW-ICSS (right) for different financial sectors.

 

일반적으로, KW-ICSS는 AIT-ICSS보다 탐지된 CP의 개수가 적어 과대탐지 현상이 줄어드는 경향을 보였다.

• 주식 시장(NASDAQ): AIT-ICSS에서 탐지된 CP 개수는 10개, KW-ICSS에서는 8개로 감소:
    KW-ICSS가 과대 탐지(over-estimation) 현상을 줄이며, 더 신뢰할 수 있는 변화점 탐지를 수행하는 것으로 보임.
• 국채 시장(20년 만기 미국 국채, US T-Bill): AIT-ICSS에서는 7개였으나, KW-ICSS에서는 5개로 줄어듬:
    국채 시장에서도 KW-ICSS가 보다 강건한 변화점 탐지를 수행함을 보임
• 통화 시장(EUDOLLR): AIT-ICSS에서는 3개였으나, KW-ICSS에서는 4개로 증가, 단 2007년경 추가된 CP는 하락 추세(빨간 점선)를 정확히 탐지함, 즉 과대 탐지는 아님.
• 원자재 시장(CRUDOIL, 원유): AIT-ICSS에서는 11개의 CP가 탐지되었으나, KW-ICSS에서는 10개로 줄었다. 특히 KW-ICSS는 2008년 금융위기 기간 동안의 변동성을 반영하면서도 불필요한 하락 추세 탐지를 줄이는 효과를 보임.

- 유의수준에 따른 변화점 탐지 성능 분석

Table 3에서 AIT-ICSS 및 KW-ICSS 알고리즘의 CP 탐지 성능을 다양한 유의수준(α=1% ~ 15%)과 금융 부문에 따라 비교하였다. 성능 평가는 탐지된 CP의 개수, CP 간 평균 간격, 단기 미래 추세 예측 성공률을 기준으로 수행되었으며, 굵은 글씨는 더 우수하거나 동등한 성능을 나타낸다.

• 각 부문별 평균 탐지된 CP 개수를 보면, 국채 시장이 가장 많고, 통화 시장이 가장 적었다.
• 모의 금융 시계열과 유사하게, 유의 수준이 증가할수록 탐지된 CP 개수도 증가하는 경향을 보였다.
• 대부분의 경우, KW-ICSS의 평균 탐지된 CP 개수가 AIT-ICSS보다 적거나 동일하였다. 단, 통화 시장에서 유의 수준 1% 및 5%에서는 KW-ICSS의 CP 개수가 더 많았다.
• 주식, 국채, 원자재 시장에서 KW-ICSS의 평균 CP 간 간격이 AIT-ICSS보다 크거나 같았다. 단, 유의 수준 13% 및 15%에서는 주식 시장에서 KW-ICSS의 평균 간격이 더 작았다.
• 원자재 시장에서는 유의 수준 5% 및 7%를 제외하고, KW-ICSS의 평균 간격이 AIT-ICSS보다 작았다.

KW-ICSS는 AIT-ICSS보다 CP를 과대탐지하는 경향이 적으며, 보다 신뢰할 수 있는 CP 탐지가 가능함을 확인하였다.

 

추세 예측 성능도 유의 수준 및 금융 부문별로 Table 3에서 분석되었다. 대부분의 경우, KW-ICSS의 단기 미래 추세 예측 성공률이 AIT-ICSS보다 높았다.
단, 다음 경우에서는 AIT-ICSS가 더 높은 성능을 보였다:

• 주식 시장(11% 유의 수준)
• 국채 및 통화 시장(13%, 15% 유의 수준)

모의 금융 시계열 실험에서, 유의 수준이 10%를 초과하면 CP 탐지의 평균 절대 편차(mean absolute deviation, MAD)가 급격히 증가하는 현상이 관찰되었다. 실제 금융 시계열에서 CP의 정확한 위치는 알려져 있지 않지만, 이를 바탕으로 유의 수준 10% 이하에서 알고리즘을 사용하는 것이 실용적으로 적절할 가능성이 크다.

 

정리하면 Table 3에서 KW-ICSS가 CP 탐지 및 추세 예측에서 AIT-ICSS보다 우수한 성능을 보였지만, 일부 금융 시계열에서는 모든 유의 수준에서 성능이 감소하는 현상도 나타났다. 따라서, 각 금융 시계열별로 과거 데이터를 기반으로 백테스트(back-testing)를 수행하여 KW-ICSS의 활용 여부를 결정하는 것이 필요하다.

 

- 전체 금융 시계열 성능 분석

Figure 5에서 전체 금융 시계열을 대상으로 KW-ICSS와 AIT-ICSS의 성능 비교를 수행하였다.

• 파란색(blue): KW-ICSS의 성능이 개선된 경우
• 노란색(yellow): KW-ICSS의 성능이 감소한 경우
• 각 금융 시장의 기호(symbols): Table 2에 정리됨

- CP 탐지 성능 비교

대부분의 유의 수준에서 KW-ICSS가 CP 탐지 성능을 향상시켰다. 그러나, 통화 및 원자재 시장에서는 일부 유의 수준에서 성능이 감소하였다. 특히, 10% 이하 유의 수준에서 다음 금융 상품의 CP 탐지 성능이 감소하였다:

• 주식 시장: FTALLSH
• 통화 시장: JAPAYE$, BRACRU$
• 원자재 시장: CORNUS2, GOLDBLN

Figure 5 - (a)

- CP 간격 비교
Figure 5-(b)에서는 탐지된 CP 개수와 CP 간격의 평균값을 비교하였다. CP 개수가 줄어들면 CP 간격이 길어지는 경향이 있기 때문에, CP 탐지 개수와 CP 간격 패턴이 유사하게 나타났다.

Figure 5 -b

- 단기 미래 추세 예측 성능 비교
Figure 5-(c)에서 대부분의 경우 KW-ICSS가 향상된 추세 예측 성능을 보였다.
그러나, 일부 금융 상품에서는 성능이 저하되었으며 특히, 유의 수준 10% 이하에서 성능이 감소한 사례는 다음과 같다:
주식 시장: TTOSP60, KORCOMP, DAXINDX
국채 시장: FRTCM1Y
통화 시장: JAPAYE$, BRACRU$

Figure 5 - c

 

C. 계산 시간 분석 (COMPUTATION TIME ANALYSIS)

KW-ICSS는 추가적인 크루스칼-왈리스(KW) 검정을 수행하기 때문에 연산량이 증가할 가능성이 있기에 따라서, 본 연구에서는 다음과 같은 방식으로 AIT-ICSS와 KW-ICSS의 계산 속도를 비교

1. 시뮬레이션 데이터(길이 1000, 5000, 10,000)에서 변화점 탐지 수행
2. 실제 금융 시계열 데이터(32개 자산, 약 4500일치 데이터)에서 알고리즘 실행
3. 각 실험에서 평균 실행 시간(average execution time)을 측정
4. 변화점 개수와 계산 시간 간의 관계를 분석

모든 실험은 Intel i7-10750H CPU (2.6GHz), 16GB RAM 환경에서 Python 3.8.5 를 사용하여 실행되었습니다.

Figure 6은 각 알고리즘의 연산 시간을 데이터 길이에 따라 비교한 그래프이다.

• x축: 데이터 길이
• y축: 실제 연산 시간(초)
• 각 금융 부문별 직선: 평균 연산 시간 (±1.5 표준편차 범위 포함)

 

표 4는 다양한 시뮬레이션 데이터 길이(N = 1000, 5000, 10,000)에 대한 AIT-ICSS 및 KW-ICSS의 평균 계산 시간(초 단위)을 비교한 결과로(첨부하지는 않음, 본 논문 참고)

 

• N=1000
  • AIT-ICSS: 평균 0.023초
  • KW-ICSS: 평균 0.029초 (+26%)
• N=5000
  
  • AIT-ICSS: 평균 0.124초
  • KW-ICSS: 평균 0.155초 (+25%)
• N=10000
  
  • AIT-ICSS: 평균 0.245초
  • KW-ICSS: 평균 0.305초 (+24%)

 

으로 나타났다. 즉, AIT-ICSS는 데이터 포인트가 5000개(약 20년치 데이터)여도 평균 1초 미만으로 CP 탐지를 수행 KW-ICSS는 동일한 데이터 길이에서 평균 약 4초 소요, 최대 6초까지 증가 가능함을 보였고, 대략적으로 금융 시계열에서 KW-ICSS가 AIT-ICSS보다 약 4배 더 긴 연산 시간을 요구함을 확인 가능했다. 
다만, KW-ICSS가 AIT-ICSS보다 연산 시간이 더 길지만, 연산 시간이 몇 초 수준내임으로, 실시간 고빈도(high-frequency) 트레이딩에도 충분히 활용 가능할 것으로 보인다. 분 단위(minutely), 시간 단위(hourly), 일 단위(daily) 투자 전략에서도 KW-ICSS를 사용할 수 있음을 의미한다. 

 

Conclusion

정리하면 아래와 같이 결론 내릴 수 있을 것이다. 

1. KW-ICSS는 AIT-ICSS 대비 CP 탐지 및 단기 미래 추세 예측 성능이 향상됨
   • 대부분의 금융 시장 및 유의 수준에서 KW-ICSS가 더 높은 성능을 보임
   • 특히 과대탐지(over-estimation) 문제가 개선됨
   • 그러나, 일부 금융 시계열에서는 성능이 감소하는 경우도 존재
2. 유의 수준 10% 이하가 실용적으로 적절
   • 모의 실험에서 유의 수준 10% 초과 시 MAD 급증
   • 실제 금융 시계열에서도 10% 이하 유의 수준에서 더 안정적인 성능을 보임
3. 연산 시간은 AIT-ICSS보다 약 4배 길지만, 실시간 트레이딩에도 충분히 활용 가능
   • KW-ICSS: 평균 4초(최대 6초), AIT-ICSS: 평균 1초 미만
   • 여전히 일반적인 실시간 고빈도(high-frequency) 트레이딩에 사용 가능 
4. 금융 시계열별로 백테스트(back-testing)를 통해 KW-ICSS 활용 여부 결정 필요
   • 일부 금융 상품에서는 모든 유의 수준에서 성능이 감소하므로, 개별적인 테스트가 필수적임

Limitaion

1. 예측 성능이 저하되는 경우 : 일부 금융 시장에서 CP 탐지 및 트렌드 예측 성능이 저하되는 경우가 있음. 따라서 KW-ICSS를 적용하려면 실무자가 대상 금융 시계열 데이터를 과거 데이터와 함께 검토하여 적용 가능성을 확인해야 함

 

2, 연산 시간: KW-ICSS는 AIT-ICSS보다 더 많은 연산 시간이 소요된다. 그럼에도 불구하고, KW-ICSS의 연산 시간은 몇 초 정도에 불과하여 실시간 고빈도 거래에도 적용 가능하다.

 

3. 벤치마크의 다양성: 본 연구는 오직 AIT-ICSS 알고리즘 개선에 초점을 맞추었으며, KW-ICSS의 성능은 AIT-ICSS와만 비교되었다. 향후 연구에서는 본 모델의 성능을 다른 유형의 비지도 이진 분할 알고리즘과 비교 평가할 필요가 있다. 또한, KW-ICSS는 모든 시계열 데이터에 적용될 수 있으므로, 향후 기후 데이터, 음성 데이터, 이미지 데이터, 의료 데이터 등의 CP 탐지 및 트렌드 예측도 확인 필요 

 

아래는 결론의 전문. 

수십 년 동안 CP 분석은 데이터 마이닝, 통계학 및 컴퓨터 과학 분야에서 연구되어 왔다. CP 분석은 여러 실제 문제에서 적절한 시점의 조치를 추정하고, 시계열 데이터에서 즉각적인 변화점을 탐지하는 것을 목표로 한다. 따라서 CP 탐지는 다양한 실무에서 필수적이다. 본 연구는 AIT-ICSS 알고리즘을 개선하여 KW-ICSS라는 이진 분할 알고리즘을 개발하는 것을 목표로 한다. CUSUM 기반 알고리즘은 CP 탐지에서 PR 곡선의 F1-score 또는 AUC, ROC 곡선을 추정하는 데 있어 가장 우수한 알고리즘 중 하나로 간주된다.

 

본 연구의 주요 기여는 두 가지로 요약될 수 있다.
첫째, 우리가 아는 한, Kruskal–Wallis (KW) 검정을 CUSUM 기반 CP 분석에 통합한 첫 번째 시도이다. KW 검정은 시계열 데이터에서 분포 변화 지점을 탐지하는 데 상대적으로 적은 양의 데이터만 필요하기 때문에 제안된 알고리즘은 회고적(오프라인) 및 실시간(온라인) 방법으로 동시에 사용할 수 있다. 또한, KW 검정은 비정규 분포 시계열 데이터를 분석할 수 있는 비모수적 비교 방법이다. 이러한 맥락에서 KW-ICSS는 비정상적 가격 변동을 실시간으로 탐지할 수 있는 일반화된 알고리즘이다.

 

둘째, KW-ICSS 알고리즘의 성능 향상과 강건성이 확인되었으며, 이는 KW 검정을 활용하는 타당성을 뒷받침한다. 실험을 통해 KW-ICSS 알고리즘이 AIT-ICSS 알고리즘보다 모의 및 실제 금융 시계열 데이터에서 더 우수한 성능을 보임을 발견하였다. CP가 알려진 모의 금융 시계열 데이터의 경우, CP 수가 증가할수록 KW-ICSS의 TPR이 AIT-ICSS보다 훨씬 높게 나타났다. 또한, KW-ICSS 알고리즘은 AIT-ICSS보다 더 적은 CP를 추정하면서도 더 높은 탐지 성능을 보였으며, 이는 알고리즘의 강건성을 시사한다. 모든 유의 수준에서 KW-ICSS의 낮은 MAD 값 역시 이러한 결과를 뒷받침한다. CP 수에 관계없이 모의 데이터에서 단기 미래 트렌드 예측 성능도 향상되었다. 따라서, KW-ICSS는 모의 금융 시계열 데이터에서 CP 탐지, 강건성 및 트렌드 예측 성능의 향상을 입증하였다. 또한, 알고리즘의 유의 수준이 10% 미만이어야 CP의 과대 추정을 방지할 수 있음을 확인하였다. CP가 알려지지 않은 실제 금융 시계열 데이터의 경우, 탐지된 CP의 평균 개수와 구간의 평균 길이를 기준으로 CP 탐지에 대한 간접적인 증거를 조사할 수 있었다. 실험 결과, KW-ICSS는 일반적으로 AIT-ICSS보다 CP 탐지에서 더 강건한 것으로 나타났다. 또한, 대부분의 금융 시장과 유의 수준에서 예측 성능이 향상되었다.

 

그러나 본 연구에는 몇 가지 한계가 존재한다.
첫 번째 한계는 일부 금융 시장에서 CP 탐지 및 트렌드 예측 성능이 저하되는 경우가 있다는 점이다. 따라서 KW-ICSS를 적용하려면 실무자가 대상 금융 시계열 데이터를 과거 데이터와 함께 검토하여 적용 가능성을 확인해야 한다.

 

두 번째 한계는 연산 시간이다. KW-ICSS는 AIT-ICSS보다 더 많은 연산 시간이 소요된다. 그럼에도 불구하고, KW-ICSS의 연산 시간은 몇 초 정도에 불과하여 실시간 고빈도 거래에도 적용 가능하다.

 

세 번째 한계는 벤치마크의 다양성이다. 본 연구는 오직 AIT-ICSS 알고리즘 개선에 초점을 맞추었으며, KW-ICSS의 성능은

AIT-ICSS와만 비교되었다. 향후 연구에서는 본 모델의 성능을 다른 유형의 비지도 이진 분할 알고리즘과 비교 평가할 필요가 있다. 또한, KW-ICSS는 모든 시계열 데이터에 적용될 수 있으므로, 향후 기후 데이터, 음성 데이터, 이미지 데이터, 의료 데이터 등의 CP 탐지 및 트렌드 예측에도 활용 가능할 것으로 기대된다.